5.3. Исследование напряженного состояния сыпучего тела

Большая часть транспортируемых и обрабатываемых с помощью вибрации грузов в различных отраслях промышленности состоит из частей, размеры которых весьма малы по сравнению с размерами рабочего органа машины. Такие грузы по общепринятой терминологии называют насыпными, распространяя на них основные положения механики сплошной среды.

Задача о виброперемещении насыпных грузов в режиме без отрыва, когда не нарушается основное условие существования сплошной среды – условие сплошности, можно, по-видимому, отнести к частной задаче механики сыпучих сред. В некоторые моменты проявляет себя и как сыпучая среда и слой груза, движущийся по рабочему органу в режиме с отрывом.

Коснемся основных закономерностей механики сыпучей среды

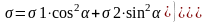
Рис. 41. Круговой график напряжений

Считают, что в любой точке сыпучего тела существуют три «главные» плоскости, в которых отсутствуют касательные напряжения , а нормальные достигают наибольшей величины σ₁>σ₂>σ₃. Сложность рассматриваемых вопросов заставляет отказываться от пространственной задачи, заменяя ее рядом плоских, т. е. σ₃=0. В любой точке среды на площадке, наклоненной к плоскости σ₁ под углом α действительные напряжения:

Сыпучее тело находится в равновесии до тех пор, пока на любой площадке каждой частицы выполняется условие:

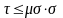
где μ_σ – коэффициент сопротивления сдвигу.

Сыпучее тело, состояние которого изображается кругом напряжений (рис. 41), соприкасающихся с кривой касательных напряжений, находится в предельном равновесии, т. е.

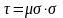
Для идеально сыпучих грузов μ_σ = μ – коэффициенту внутреннего или внешнего трения.

При нарушении равновесия сыпучее тело или его отдельные элементы перейдут в состояние текучести, сопровождающееся скольжением частиц по площадкам, наклоненным к площадке напряжения σ₁ под углом CO₁D₁=2ψ.

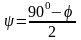
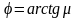– угол трения.

Совокупность таких площадок образует поверхность скольжения.

.

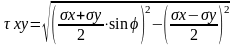Исходными данными в задачах о напряженном состоянии обычно бывает либо давление рабочего органа, либо, при отсутствии вибрации, гидростатическое давление:

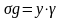
где y – отстояние от свободной поверхности слоя; γ – насыпной вес груза.

Напряжение вызывает появление бокового давления σ_б.

Отношение 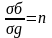– коэффициент бокового давления. Если σ_g и σ_б являются одновременно и главными, т. е. 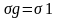, а 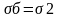,то n принимает свое наименьшее значение, называясь коэффициентом подвижности m. Максимальное значение n, если 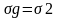, а 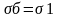. Это возможно, если тело помещено в сосуд с податливой стенкой. При увеличении σ_g стенка может перемещаться и груз без нарушения равновесия способен воспринять значительно большее боковое давление, называемое в этом случае пассивным. Величина σ_б при постоянном σ_g может меняться в следующих пределах без нарушения равновесия:

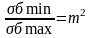
Для идеально сыпучих грузов:

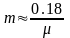
Напряженное состояние сыпучего тела, находящегося в виброжелобе.

Рис. 42. Эпюры давления груза на дно и стенки сосуда

Рассмотрим случай, когда сыпучее тело сформировано без предварительного уплотнения в горизонтальном сосуде с прямолинейными вертикальными стенками (рис. 42).

Касательные напряжения τyc в плоскости стенки желоба, вследствие оседания нижних слоев воспринимает часть веса груза. Давление на дно, у стенки, несколько меньшее: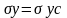 . Наличие τyc влечет и некоторое отклонение от вертикали на угол χ траекторий главных напряжений (кривые 1). Направление возможных пластических деформаций показывает сетка линий скольжения (кривые 2 и 3).

При воздействии горизонтальной составляющей вибрации траектории главных напряжений периодически отклоняются еще и в продольной плоскости желоба, дополнительно искривляясь. Нарушение предельного равновесия и пластическое течение в слое происходит не одновременно во всем слое и не в равной мере. Образуются отдельные монослои с частицами. Имеющими равный или близкий комплекс динамических условий связи.

Границами монослоев становятся поверхности скольжения (поверхности, проходящие через частицы равных условий связи). Это согласуется с результатами экспериментального исследования методом парафинирования.

Верхняя часть слоя, ограниченная снизу поверхностями скольжения, проходящими через линии соприкосновения свободной поверхности груза со стенками желоба, находится в особых условиях. На нее оказывает влияние пристеночное трение, она практически не воспринимает пассивного бокового давления. Движение этой части носит особый характер.

Рассмотрим напряженное состояние сыпучего тела в поперечной плоскости желоба. Не будем учитывать горизонтальные составляющие вибрации.

Введем понятие динамического объемного веса:

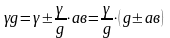
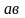– ускорение вертикальных колебаний.

Вертикальное давление у дна:

.

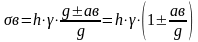Если меняется от 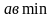до 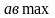, то давление достигает:

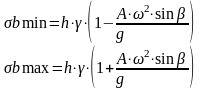
где А – амплитуда; ω – частота гармонических колебаний желоба.

Рис. 43. Круговой график напряжений

Предельное напряженное состояние в статике характеризуется овалом или кругом напряжений (рис. 43). При воздействии вибрации вертикальная составляющая давления 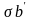достигнет наибольшей величины при sinωt=1. В этот момент возникнет наибольшее боковое давление 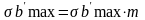, затем должно следовать уменьшение давления. Однако, если режим вибрации не весьма интенсивен, боковое давление достигнув 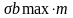в дальнейшем может не уменьшаться. Таким образом, в безотрывном режиме груз, уплотнившийся за счет давления и трения у стенки, может избегнуть разрыхления. В рассматриваемом состоянии на слой действует значительное пристеночное трение.

Возможен момент, когда окажется меньше чем , т. е. из активного превратится в пассивное, способное выдавить частицы груза вверх.

.

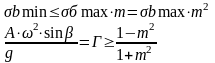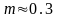
Для песка при , при котором возникает эффект периодического разрыхления равен не 1, а 0,84. Следовательно, условием отрыва предшествуют режимы с интенсивным перемешиванием. Наличие бокового давления, а следовательно и пристеночного трения хотя и влияют на характеристики микрополетов слоев, но не нарушают в большую сторону критерий возникновения отрыва.