
- •Влияние вибрации на технологические процессы с разработкой методических основ проектирования оборудования
- •240801.65 – Машины и аппараты химических производств
- •150400.68 – Технологические машины и оборудование
- •Введение
- •Глава Колебания и вибрация
- •1.1. Общие сведения о колебаниях и вибрации как о механических явлениях
- •1.2. Использование полезных свойств вибрации
- •1.3. Основные виды процессов и машин, область их применения
- •Глава Виды колебаний
- •2.1. Классификация колебаний
- •2.2. Свободные колебания
- •2.2.1. Общие сведения о свободных колебаниях
- •2.2.2. Свободные колебания системы с одной степенью свободы без трения
- •2.2.3. Свободные колебания, сухое трение
- •Позиционное трение
- •2.2.4. Вязкое трение
- •2.3. Вынужденные колебания
- •Глава Колебательные системы
- •3.1. Виды колебательных систем
- •3.2. Основные характеристики колебательной системы
- •Приведенная жесткость
- •Параллельное соединение
- •Последовательное соединение
- •Приведенные значения
- •Глава IV Основы теории вибрационного перемещения частицы
- •4.1. Эффекты вибрационного перемещения, используемые в технологических процессах
- •4.2. Уравнения движения материальной точки по плоскости, совершающей продольные гармонические колебания, режимы виброперемещения
- •4.3. Условия возникновения движения, асимметрия системы
- •Глава V Экспериментальное исследование процесса виброперемещения слоя насыпного груза
- •5.1. Методики проведения экспериментов
- •5.2. Результаты экспериментальных исследований
- •5.3. Исследование напряженного состояния сыпучего тела
- •Глава VI Математическое моделирование процесса виброперемещения
- •6.1. Механические свойства сыпучих тел
- •Деформация сыпучих тел
- •Сопротивление сыпучего тела сдвигу, внутреннее трение и сцепление.
- •6.2. Свойства обрабатываемых грузов под действием вибрации
- •6.3. Реологические свойства обрабатываемых продуктов
- •6.4. Выбор модели слоя транспортируемого груза
- •6.5. Теоретическое исследование процесса вибрационного перемещения модели слоя сыпучего груза
- •Методика проектирования вибрационных транспортирующих машин
- •Глава VII Вибровозбудители
- •7.1. Классификация вибровозбудителей
- •7.2. Инерционные вибровозбудители
- •7.3. Эксцентриковые вибровозбудители
- •Конструкции вибраторов.
- •7.4. Электромагнитные вибровозбудители
- •7.5. Поршневые вибровозбудители
- •7.6. Высокочастотные вибровозбудители
- •Приложения Приложение 1 Методика расчета центробежных вибровозбудителей
- •Приложение 2 Методика расчета кинематического вибровозбудителя
- •Приложение 3 Методика расчета гидравлического вибровозбудителя
- •Приложение 4 Методика расчета электромагнитного вибровозбудителя
- •Приложение 5 Методика расчета электродинамического вибровозбудителя
- •Приложение 6 Методика расчета виброориентаторов пищевых машин Алгоритм расчета
- •Ориентирование рыбы на наклонном лотке
- •Ориентирование рыбы на планках, движущихся в противофазе
- •Круговой ориентатор
- •Ориентирование рыбы на планках, движущихся в одном направлении с разной интенсивностью
- •Приложение 7 Методика расчета транспортирующих устройств
- •Режимы движения и фазовые углы
- •Приложение 8 Алгоритм расчета виброизоляции набивочной машины для укладки порций рыбы в банки
- •Приложение 9 Алгоритм расчета вибрационного питателя набивочной машины ина-115
- •Приложение 10 Вибрационное уплотнение рыбы
- •Приложение 11 Понятие о динамическом гасителе колебаний
- •Приложение 12 Колебания лопаток турбомашин
- •Приложение 13 Основы расчета виброизоляции
- •Приложение 14 Исследование работы вибрационного питателя с бункером
- •Условия движения слоя мелкозернистого материала
- •Приложение 15 Алгоритм расчета вибрационного смесителя с тороидной камерой
- •Список рекомендуемой литературы
Приведенная жесткость
Важной характеристикой любого упругого элемента при деформациях является коэффициент жесткости:
– при
продольных деформациях
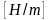
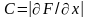
где
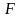 – восстанавливающая сила,
– линейная деформация при крутильных
деформациях
– восстанавливающая сила,
– линейная деформация при крутильных
деформациях
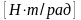 .
.
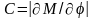
где
 –
восстанавливающий момент,
– угловая деформация.
–
восстанавливающий момент,
– угловая деформация.
Величина
обратная жесткости
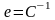 называется
коэффициентом податливости.
называется
коэффициентом податливости.
Типичные
графики восстанавливающей силы
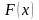 ,
которым соответствуют графики жесткости
,
которым соответствуют графики жесткости
 показаны
на рис. 27, а,
б.
показаны
на рис. 27, а,
б.


а б
Рис. 27. Графики восстанавливающей силы
Вид функции определяется материалом и конструктивными особенностями упругого элемента. Так, например, в рабочем диапазоне напряжений металлы обычно подчиняются закону Гука (кривая 1), для резины более свойственна жесткая характеристика (кривая 2), для многих полимеров – мягкая (кривая 3).
Однако в конструкциях, состоящих только из металлических деталей, также возможно возникновение нелинейных восстанавливающих сил. Это наблюдается при точечном или линейном контакте двух поверхностей, что характерно для элементов высших кинематических пар. В этом случае контактная жесткость увеличивается с ростом нагрузок. Нарушение линейной характеристики восстанавливающей силы может происходить из-за использовании специальных выбранных нелинейных упругих элементов -конических пружин, нелинейных муфт, из-за подключения или отключения каких-либо элементов кинематической цепи, наличие зазоров в кинематических парах, упоров, фиксаторов и других факторов.
Приведение упругих характеристик имеет своей целью упрощение моделей и возможно лишь в том случае, когда деформация упругих элементов зависит от одной и той же обобщенной координаты.
Параллельное соединение

Рис. 28. Параллельное соединение упругих элементов
Свойства параллельного соединения (рис. 28) – равенство абсолютных значений деформаций:
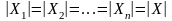
При приведении не должен нарушаться баланс потенциальной энергии системы.
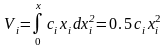
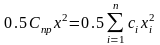
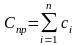
Последовательное соединение


Рис. 29. Последовательное соединение упругих элементов
Свойство последовательного соединения (рис. 29) – равенство передаваемых сил.
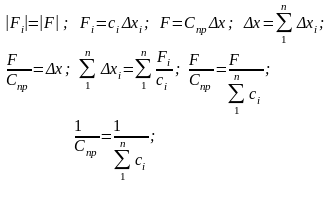
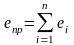 .
.
При параллельном соединении определяющую роль играют наиболее жесткие элементы, а при последовательном – наиболее податливые.
Коэффициенты жесткости отдельных типовых звеньев приводятся в справочниках, где даются данные для их расчета, или приводится диапазон возможных изменений их величины.
Диссипативные силы.
Рассеивание
энергии при колебаниях оценивается
коэффициентом поглощения равным
отношению двух последовательных
максимальных амплитуд
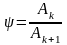 или
логарифмическим декрементом колебаний
или
логарифмическим декрементом колебаний
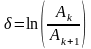
Коэффициент
поглощения
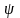 и
и
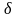 определяются
экспериментально и приводятся в
справочной литературе для отдельных
элементов или для механизма в целом.
Например, для сухих цилиндрических и
конических стыков
определяются
экспериментально и приводятся в
справочной литературе для отдельных
элементов или для механизма в целом.
Например, для сухих цилиндрических и
конических стыков
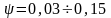 ;
для подшипников качения усредненное
значение
;
для подшипников качения усредненное
значение
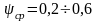 .
.
Для
многих механизмов
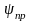 находится
в диапазоне
находится
в диапазоне
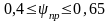 .
.
В общем случае параметры диссипации не являются константами.
При
решении инженерных задач в уравнение
движения силы трения (сопротивления
движению) вводят в виде линеаризованной
силы, пропорциональной скорости
 ,
где «
,
где «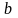 »
– коэффициент пропорциональности,
размерностью
»
– коэффициент пропорциональности,
размерностью
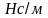 или
или
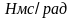 .
Коэффициент «
»
может быть определен, как
.
Коэффициент «
»
может быть определен, как
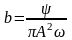 ,
где
– площадь петли гистерезиса.
,
где
– площадь петли гистерезиса.
Отношение
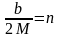 называется коэффициентом
демпфирования.
называется коэффициентом
демпфирования.
Логарифмический декремент колебаний, может быть определен через коэффициент демпфирования
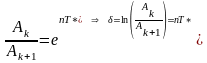 ,
где
,
где
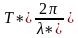 - период
времени между двумя максимальными
смещениями (амплитудами);
- период
времени между двумя максимальными
смещениями (амплитудами);
 – собственная
частота колебаний
демпфированной системы.
– собственная
частота колебаний
демпфированной системы.
Связь между и устанавливается соотношениями:
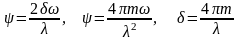 или
по приближенному выражению
или
по приближенному выражению
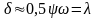 .
.
Величина
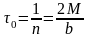 называется постоянной времени.
называется постоянной времени.
Число
колебаний при затухании определяется,
как
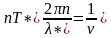
Отношение
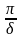 называется
добротностью
системы.
Чем меньше
,
тем больше добротность системы и тем
больше амплитуда вынужденных колебаний
в зоне резонанса.
называется
добротностью
системы.
Чем меньше
,
тем больше добротность системы и тем
больше амплитуда вынужденных колебаний
в зоне резонанса.
При
режимах далеких от резонанса ( или
или
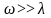 )
затухание мало влияет на коэффициент
динамичности.
)
затухание мало влияет на коэффициент
динамичности.
Частота
затухающих колебаний
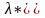 мало
отличается от частоты
мало
отличается от частоты
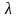 собственных
колебаний соответствующей консервативной
системы.
собственных
колебаний соответствующей консервативной
системы.
