Позиционное трение

Так называется вид трения, при котором сила трения пропорциональна смещению. Рассмотрим систему, состоящую из груза массой m, закреплённого на рессоре, листы которой собраны без предварительного натяга (рис. 21, а). Сила трения листов рессоры друг от друга пропорциональна контактному давлению, которое, в свою очередь, пропорционально смещению X. Зависимость между реакцией рессоры, действующей на груз, и смещением груза F=f (X) для рассматриваемой системы представлена на рис. 21, б.

Обозначим жёсткость системы при увеличении смещения X по модулю через С₁, а жёсткость при уменьшении абсолютного значения смещения - через С₂. Жёсткость упругого элемента системы при отсутствии трения C₀ = ( C₁ + C₂ ) / 2.

а б

Рис. 21. Исследование свободных колебаний

На каждой четверти периода характеристика системы прямолинейна, поэтому движение массы m описывается синусоидой. При переходе через равновесное положение частота собственных колебаний меняется от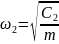 до 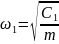. Отклоним массу m в крайнее правое положение, при этом её скорость в этот момент 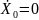. Если груз отпустить, то он начнёт двигаться влево под действием силы упругости, уменьшенной на величину сил трения. Частота собственных колебаний груза будет ω₂, а время движения до равновесного положения - . Скорость груза в равновесном положении станет равной ω₂A. Дальнейшее движение (влево) определяется жёсткостью C₁, а крайнего левого положения груз достигает через время . Наибольшее смещение влево равно ω ₂A/ ω ₁.

Максимальное отклонение вправо в конце полного периода движения вычисляется по формуле

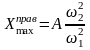
следовательно, логарифмический декремент колебаний:

.

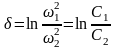При малом затухании, когда разность жесткостей C₁ – C₂ существенно меньше средней жёсткости C₀, получим

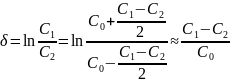
Характер движения при позиционном трении показан на рис. 22. Из полученных формул следует, что при силе трения, пропорциональной смещению, логарифмический декремент колебаний постоянен и, следовательно, точно так же, как и при вязком трении, последовательные амплитуды составляют геометрическую прогрессию.

Рис. 22. Зависимость перемещения от времени.

Как видно из рис. 22, период рассматриваемых затухающих колебаний:

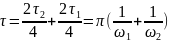
Соответствующая этому периоду угловая частота:

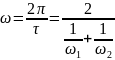
Частоты ω₁ и ω₂ определяются выражениями

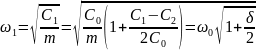
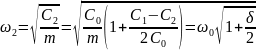
где 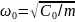- собственная частота соответствующей системы без трения.

Тогда

.

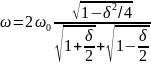При небольших логарифмических декрементах колебаний δ это выражение отличается от собственной частоты колебаний соответствующей системы без трения на величину второго порядка малости. Поэтому подобно вязкому и сухому трению позиционное трение практически не влияет на собственную частоту колебаний

2.2.4. Вязкое трение

В этом случае возникает сопротивление движению, которое пропорционально его скорости. При этом сила сопротивления описывается выражением

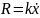(13)

где k – коэффициент пропорциональности.

Примером системы, работающей в условиях вязкого трения, может служить гидравлический амортизатор (рис. 23), который создаёт сопротивление движению поршня, зависящее не от перемещения (как это свойственно упругим связям), а от скорости и пропорционально её первой степени (8). Подобные устройства применяются, например, в конструкциях автомобильной подвески. Гидравлический амортизатор состоит из одного или нескольких цилиндров с поршнями или из камеры, в которой может вращаться крыльчатка. Цилиндры и камера наполнены амортизационной жидкостью. При движении поршней или крыльчатки эта жидкость продавливается через калиброванные отверстия; этим создаётся сопротивление, по характеру близкое к вязкому. В формуле (8) R – это сила, действующая на амортизатор, а вязкая реакция амортизатора на колеблющееся тело имеет противоположное направление.

Рис. 23. Система с вязким трением.

Дифференциальное уравнение движения в рассматриваемом случае таково:

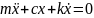(14)

или

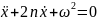(15)

где ; .

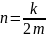Для рассматриваемого линейного дифференциального уравнения с постоянными коэффициентами характеристическое уравнение имеет вид

,

.

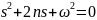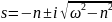Обозначим

.

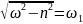Тогда решение уравнения (15) определяется формулой

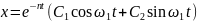(16)

или

(17)

где ; .

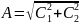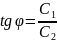Следовательно, при наличии вязкого трения движение груза описывается непериодическим законом (рис. 24).

Тем не менее часто это движение называют периодическими затухающими колебаниями, несмотря на очевидную невозможность совмещения понятий «периодические» и «затухающие».

Рис. 24. Закон движения системы с вязким трением.

Под периодом ₁ этих колебаний понимают время между двумя максимальными смещениями:

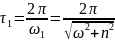(18)

Величину ₁ называют угловой частотой затухающих колебаний.

Отношение двух последовательных максимальных отклонений от положения равновесия

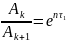(19)

Значит, последовательные максимальные отклонения системы от равновесного положения (амплитуды колебаний) представляют собой члены геометрической прогрессии со знаменателем, равным . Чаще рассматривают не отношение двух последовательных амплитуд, а логарифм этого отношения, который называют логарифмическим декрементом колебаний:

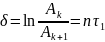(20)

В металлических конструкциях без специально введенных элементов трения логарифмический декремент составляет обычно от нескольких сотых до десятых долей единицы.

Если колебания затухают медленно и отношение двух последовательных амплитуд 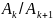близко к единице, то

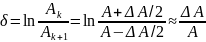
где ; .

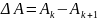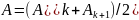Таким образом, при малом затухании логарифмический декремент примерно равен отношению изменения амплитуды колебаний за период τ₁ к амплитуде А.

Так как логарифмический декремент колебаний

,

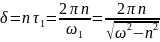то

.

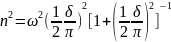Подставляя значение n² в формулу для ω₁, установим связь между величинами ω₁, ω и δ:

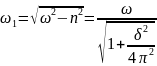(21)

Из (16) следует, что даже при значительном затухании частота ₁ затухающих колебаний мало отличается от частоты собственных колебаний соответствующей системы без трения. Например, при сравнительно большом затухании, когда каждый следующий размах вдвое меньше предыдущего (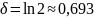 ), частота ω₁ лишь на 0,6 % меньше, чем ω. Таким образом, можно считать, что трение практически не влияет на частоту колебаний и ω₁ ~ ω.

Определим постоянные интегрирования в решении уравнения затухающих колебаний (17). Обозначим смещение и скорость в начальный момент времени t₀=0 через x₀ и 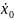соответственно. Тогда

x₀= C₁;   ,

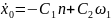C₁= x₀;       ,

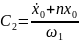и решение уравнения (21) , удовлетворяющее начальным условиям, имеет вид

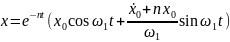(22)