19. Образование шарнира пластичности при изгибе.

После исчерпания упругой работы в сплошных изгибаемых элементах, выполненных из пластичных сталей, пластические деформации распространяются в глубь сечения (рис. 2.14) и в предельном состоянии пронизывают все сечение, образуя шарнир пластичности.

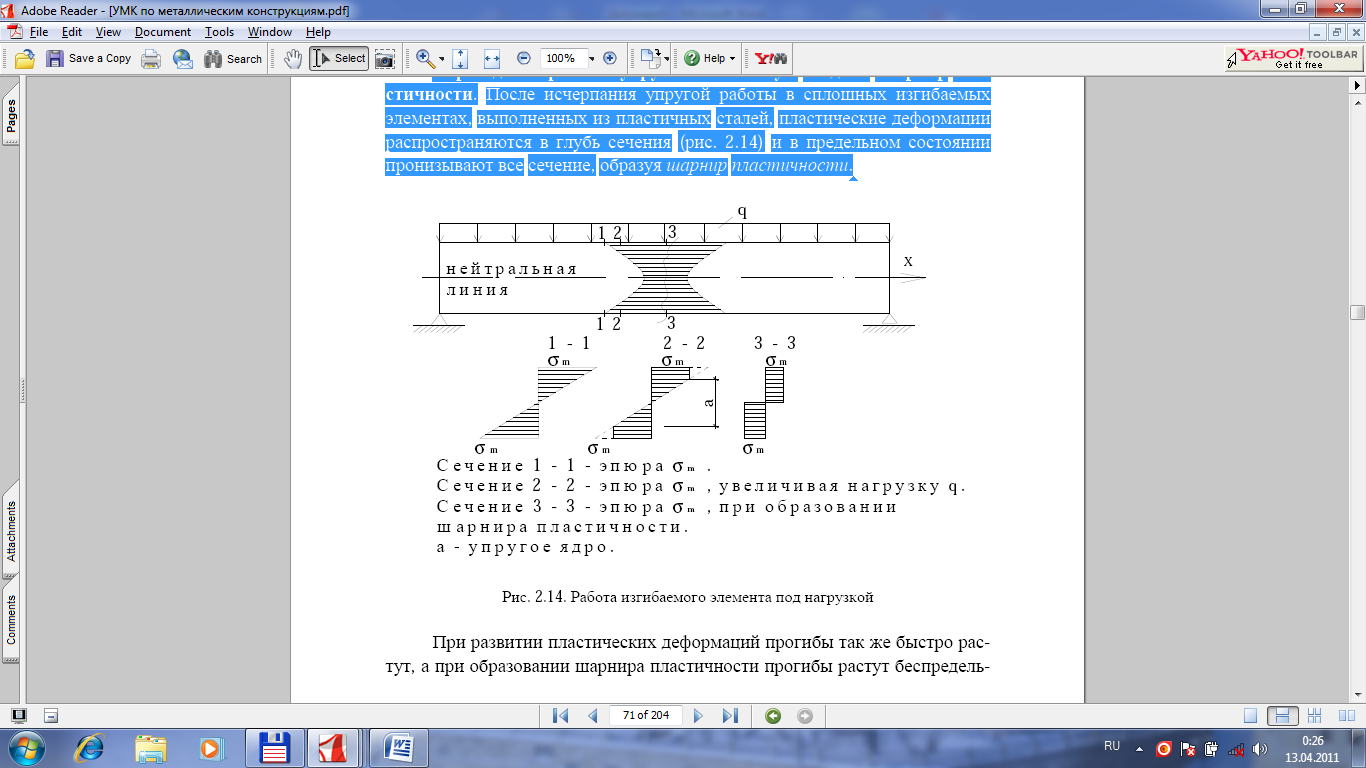
При развитии пластических деформаций прогибы так же быстро растут, а при образовании шарнира пластичности прогибы растут беспредельно. Эпюра напряжений такого состояния имеет вид двух прямоугольников. Тогда предельный момент внутренних сил определяется из выражения:

M_lim =

В упругой стадии M_x = σ_тW_x .

С учётом развития пластических деформаций условие прочности имеет вид: ≤ R_y

где W_pl = C₁×W_x или C₁=W_pl /W_x ; С₁ – коэффициент, учитывающий развитие пластических деформаций; W_pl – пластический момент сопротивлений; W_x – упругий момент сопротивлений.

20. Совместное действие нормальных и касательных напряжений.

При совместном действии изгибающего момента и поперечной силы условие образования шарнира пластичности определяется некоторой функцией, имеющей достаточно громоздкие вычисления. Поэтому для упрощения расчета, с достаточной точностью вычислений (с небольшим запасом), распространение пластических деформаций по стенке учитывают эквивалентным повышение расчетного сопротивления на 15 %.

В общем случае приведенные напряжения в стенке балок при действии нормальных напряжений в двух направлениях σ_x и σ_y и касательных напряжений τ _xy проверяют по формуле

При этом каждое из напряжений не должно превышать расчетного сопротивления, то есть:

где σ_x=M_x / I_x – нормальное напряжение, параллельное оси балки; где I_x – осевой момент инерции; σ_y – напряжения, в местах приложения сосредоточенных нагрузок к верхнему поясу, а также в опорных сечениях балки, не укрепленных ребрами жесткости;

τ_xy =Q·S / I·t – касательное напряжение; где t – толщина стенки; S – статический момент отсеченной части;Q – поперечная сила; I – толщина.

Для разрезных балок дальнейшее увеличение нагрузки невозможно, так как наступает предельное состояние первой группы (по несущей способности и непригодности к эксплуатации) вследствие чрезмерного развития пластических деформаций. Для неразрезных балок образование шарнира пластичности приводит к перераспределению моментов и понижению степени статической неопределимости конструкции.

21. Особенности расчета изгибаемых элементов на прочность в упругой стадии и с учетом развития пластических деформаций.

Расчет на прочность элементов (кроме балок с гибкой стенкой, с перфорированной стенкой и подкрановых балок), изгибаемых в одной из главных плоскостей, следует выполнять по формуле

Значение касательных напряжений τ в сечениях изгибаемых элементов должны удовлетворять условию

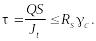
При наличии ослабления стенки отверстиями для болтов значения τ следует умножать на коэффициент α, определяемый по формуле

α = a/(a – d), где a – шаг отверстий; d – диаметр отверстия.

Для расчета на прочность стенки балки в местах приложения нагрузки к верхнему поясу, а также в опорных сечениях балки, не укрепленных ребрами жесткости, следует определять местное напряжение σ_ioc по формуле где F – расчетное значение нагрузки (силы); l_ef – условная длина распределения нагрузки, определяемая в зависимости от условий опирания; для случая опирания на верхний пояс l_ef=b+2t_f, t_f – толщина верхнего пояса балки.

Расчет на устойчивость балок двутаврового сечения, изгибаемых в плоскости стенки, следует выполнять по формуле

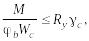
где W_c – следует определять для сжатого пояса.

Расчет на прочность разрезных балок сплошного сечения из стали с пределом текучести до 530 МПа, несущих статическую нагрузку, следует выполнять с учетом развития пластических деформаций по формулам:

- при изгибе в одной из главных плоскостей при касательных напряжениях 0,9 (кроме опорных сечений)

- при изгибе в двух главных плоскостях при касательных напряжениях 0,5 (кроме опорных сечений) здесь и - абсолютные значения изгибающих моментов