15. Нормативные сопротивления материала по пределу текучести и временному сопротивлению.

16. Расчет конструкций по предельным состояниям второй группы.

К предельным состояниям второй группы относятся состояния, затрудняющие нормальную эксплуатацию конструкции или снижающие их долговечность вследствие появления недопустимых прогибов, углов поворота, колебаний, трещин. Эти предельные состояния характеризуются неравенством:

δ ≤ δ_пред

где δ – деформация или перемещение от нормативных нагрузок (зависят от нагрузок, св-в материала, геометрических размеров и расчетной схемы конструкции);

δ_пред – предельная деформация или перемещение, ограничивающие нормальную эксплуатацию (зависят от назначения конструкции).

Предельные деформации металлических конструкций и элементов устанавливают указанные главы СНиП.

17. Работа и расчет на прочность центрально-нагруженных элементов. Одним из наиболее распространённых сооружений являются стержневые конструкции, состоящие из таких элементов, два измерения которых значительно меньше третьего.

К стержневым сооружениям относятся балки, арки, фермы, рамы и т.д. Стержни, сжатые осевой силой рассчитывают по первому предельному состоянию:

‒ по прочности: σ = ≤ R_y ∙ γ_c, если ≤ 6;

‒ по устойчивости: σ = 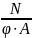≤ R_y ∙ γ_c, если > 6

где А – площадь сечения; φ – определяется по [1] в зависимости от условной гибкости λ.

Условная гибкость определяется по формуле: ,

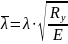где λ – гибкость, т.е. λ = l_ef /i; E – модуль упругости; i = 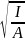– радиус инерции; l_ef – расчетная длина стержня; А – площадь сечения; I – осевой момент инерции.

Расчетная длина стержня зависит от условий его закрепления и определяется по формуле: l_ef = l_c μ,

где l_c – длина стойки; μ – коэффициент приведения к расчетной длине, зависящий от способов закрепления стержня, например, с шарнирно опертыми концами стойки μ = 1.

Для стержней со сплошной стенкой значения условной гибкости λ при вычислении коэффициента φ по формулам из [1] определяется в трех случаях:

1. При 0 ˂ 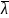≤ 2,5; φ = 1 ‒ (0,073 ‒ 5,53 ) ∙ ∙

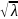
2. При 2,5 ˂ ≤ 4,5;

φ = 1,47 ‒ 13,0 ‒ (0,371 ‒ 27,3 ) ∙ + (0,0275 ‒ 5,53 ) ∙ ²

3. При > 4,5; φ =

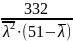
Численное значение φ для элементов из стали с расчетным сопротивлением R_y от 200 до 640 МПа, приведены в [1, табл. 72, с. 80].

18. Работа изгибаемых элементов в упругой и упругопластической стадиях.

Установлено, что при σ_Т /σ_В ≤ 0,75 после упругой работы и небольшой переходной стадии наступает пластическое течение, что на диаграмме отмечается протяжённой площадкой текучести. В целях упрощения расчётных предпосылок при работе конструкции в упругопластической стадии диаграмма работы стали уподоблена работе идеального упругого тела, которое совершенно упруго до предела текучести и совершенно пластично после него.

При одноосном напряжённом состоянии переход в пластическую стадию происходит при достижении нормальным напряжением предела текучести. При многоосном напряжённом состоянии переход в пластическую стадию зависит не от одного напряжения, а от функции напряжений, характеризующих условия пластичности.

Работе стали и алюминиевых сплавов наиболее близки третья и четвертая теории прочности. В [1] принята четвертая, энергетическая теория прочности. По этой теории пластичность наступает тогда, когда работа изменения формы тела достигает наибольшей величины.

На основе четвертой теории прочности, одноосное приведённое напряжение, эквивалентное по переходу материала в пластическое состояние данному сложному напряжённому состоянию, определяется в главных напряжениях, а также может быть выражено в нормальных и касательных напряжениях:

σ_ef = R_yn,

σ_ef =

Отсюда при изгибе (вдали от точек приложения нагрузки), когда σ_x ≠ 0;

τ_xy ≠ 0, то условие пластичности запишется в следующем виде:

σ_ef =

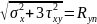
При простом сдвиге σ_x = 0:

σ_ef =

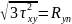
τ_xy =

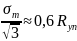
По третьей теории прочности τ_xy ≈ 0,5σ_m, где σ_m – предел текучести.