Момент силы относительно оси

Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.

Единицы измерения

Момент силы измеряется в ньютон-метрах. 1 Н·м — момент силы, который производит сила 1 Н на рычаг длиной 1 м. Сила приложена к концу рычага и направлена перпендикулярно ему.

Билет №22

Момент импульса материальной точки относительно точки O определяется векторным произведением , где   — радиус-вектор, проведенный из точки O,   — импульс материальной точки. Момент импульса материальной точки относительно неподвижной оси    равен проекции на эту ось вектора момента импульса, определенного относительно произвольной точки O данной оси. Значение момента импульса    не зависит от положения точки O на оси z.

Билет №23

Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем.

Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.

В упрощённом виде:  , если система находится в равновесии.

Билет №24 Работа и мощность вращающихся тел

За время dt вращающееся тело совершит работу dA, равную произведению момента силы M на угол поворота , сделанный радиусом этого тела, то есть

.                                                          (1.16)

Работу, совершенную вращающимся телом за единицу времени, называют мощностью вращающегося тела N, то есть

, ,

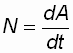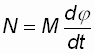где – мгновенное значение угловой скорости .

Поэтому

(1.17)

Билет №25

25. Основной закон динамики вращательного движения.

Пусть твердое тело вращается относительно неподвижной оси Оz, тогда

dA=dE_k (работу можно найти как изменение кинетической энергии)

M_{z *}dφ=d(I_zω²)=I_z *ω*dω Поделим все на dt, учитывая что dφ/dt=ω (угловая скорость)

и dω/dt=ε (угловое ускорение), тогда

M_z=I_{z *}ε –основное уравнение динамики вращательного движения

Где M_z – сумма моментов импульсов

I_z – момент инерции тела относительно оси Oz

ε - угловое ускорение тела.

Билет №26

Свободные оси (оси свободного вращения) – оси, ориентация которых в пространстве не изменяется без действия на них внешних сил.

В любом теле существует три взаимно перпендикулярных оси, проходящих через центр масс тела – свободные оси или главные оси инерции.

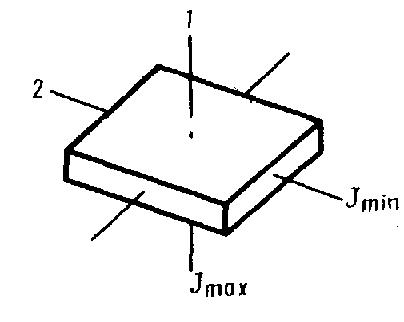
Для устойчивого вращения тела имеет значение каков момент инерции тела относительно выбранной оси вращения.

Устойчивое вращение – вращение вокруг осей с максимальным и минимальним моментами инерции.

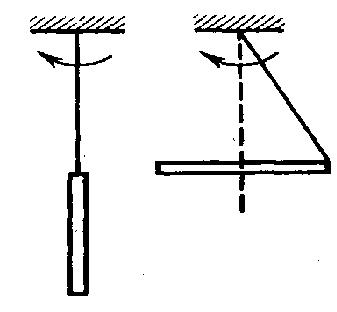
Примером применения свободных осей служит гироскоп.

Гироскоп – однородное массивное тело, вращающееся с большой угловой скоростью вокруг своей оси симметрии – свободной оси.

Если гироскоп не вращается, то оси его можно придать любое направление в пространстве. Если же он вращается, то кратковременно действие на ось гироскопа парой сил не изменит ее направления.

dL_z/dt = M_z

Момент силы тяжести относительно закрепленной оси равен 0.

M_z=0 отсюда L_z=const

Гироскопический эффект.

dL₌M*dt

L=L+dL (все векторно)

За счет возникновения нового направления момента импульса ось гироскопа поворачивается вокруг оси О₃, а не вокруг О₂ как ожидалось.