
- •Билет №1
- •Билет №2
- •Билет №3
- •Билет №4
- •Билет №5
- •Билет №6
- •Билет №7
- •Билет №9 Силы в механике
- •Билет №15
- •Билет №16
- •Билет №17
- •Билет №18
- •Билет №19 кинетическая энергия вращательного движения твердого тела
- •Кинетическая энергия при плоском движении
- •Билет №20 Абсолютно упругий удар
- •Абсолютно неупругий удар
- •Билет №21 Общие сведения
- •Момент силы относительно точки
- •Момент силы относительно оси
- •Единицы измерения
- •Билет №22
- •Билет №23
- •Билет №24 Работа и мощность вращающихся тел
- •Билет №25
- •25. Основной закон динамики вращательного движения.
- •Билет №26
- •Билет №27
- •Билет №28
- •Билет №29
- •Билет №30
- •Билет №31
- •Билет №32
- •Билет №33
Билет №1
Материальная точка- тело, массой размерами и формой которого можно пренебречь.
Система материальных точек: произвольное тело или систему тел можно разбить на мало взаимодействующие между собой части, каждую из которых можно считать материальной точкой.
Любое движение можно представить как комбинацию поступательного и вращательного движения.
Поступательное движение – это движение, при котором любая прямая жестко связанная с телом остается параллельна своему первоначальному положению.
Вращательное движение тел - называется движение, при котором все точки тела движутся по окружности, центры которых находятся на одной и той же прямой названной осью вращения.
Билет №2
Движение тел происходит в пространстве и во времени.
Тело отсчета – произвольно выбранное тело относительно, которого рассматривается положение других тел.
Система отсчета – совокупность системы координат и часов, связанных с телом отсчета.
Положение о пространстве и времени в классе механика:
1Пространство трехмерно и евклидово
2Пространство однородно
3Пространство изотропно
4Пространство абсолютно
5Время одномерно
6Время однородно
7Время абсолютно
Билет №3
Существует 3 способа задания движения
1.Векторный
Положение материальной точки задается радиус вектор из некоторой неподвижной точки системы отсчета к данной материальной точке.
При движении материальной точки радиус вектор изменяется как по направлению так и по модулю.
Радиус вектор задается как функция времени.
r = r(t).
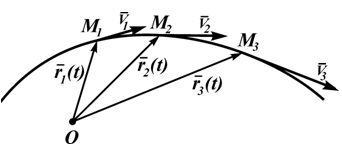
Траектория - геометрическое место концов радиус вектора
Пример: r(t) = x(t)i +y(t)j+z(t)k
2.Координатный
С выбранным телом отсчета связывается любая система координат.
Пусть выбрана прямоугольная система координат
x=x(t)
y=y(t) (1.4)
z=z(t)
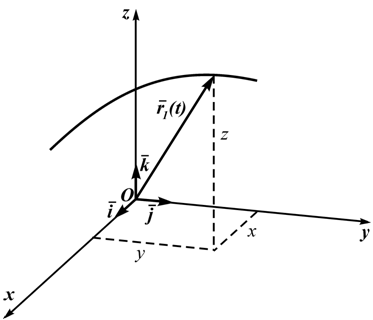
r(t)=i⋅x(t) ⊕ j⋅y(t) ⊕ k⋅z(t) (1.5)
r=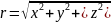
3.Естественный
Заранее известна траектория движения положение точки задается криволинейной координатой
Траектория криволинейная

S=S(t).
Билет №4
Путь (длина пути) ∆s - длина участка траектории, пройденного материальной точкой с момента начала отсчета времени (является скалярной функцией времени∆s=∆s(t)).
Перемещением называется вектор ∆r = r – r0 ,проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени).
Вектор элементарного перемещения материальной точки траектория за малый промежуток времени.
dr=│dr│=dS
Вектор dr по касательной
Скорость
Для характеристики
движения материальной точки
вводится векторная величина —
скорость, которой определяется
как быстрота движения,
так и его направление в
данный момент времени.
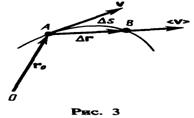
Пусть
материальная точка движется по какой-либо
криволинейной траектории так, что в
момент времени t ей
соответствует радиус-вектор r0(рис 3) В
течение малого промежутка времени
Dtточка
пройдет путь Ds и
получит элементарное (бесконечно малое)
перемещение Dr.
Вектором
средней скорости <v>
называется отношение приращения Dr
радиуса-вектора точки к промежутку
времени Dt:
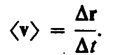 Направление вектора средней
скорости совпадает с направлением Dr.
При неограниченном уменьшении
Dt средняя
скорость стремится к предельному
значению, которое называетсямгновенной
скоростью v:
Направление вектора средней
скорости совпадает с направлением Dr.
При неограниченном уменьшении
Dt средняя
скорость стремится к предельному
значению, которое называетсямгновенной
скоростью v:
 Мгновенная скорость v, таким
образом, есть векторная величина, равная
первой производной радиуса-вектора
движущейся точки по времени. Так как
секущая в пределе совпадает с
касательной, то вектор скорости v
направлен по касательной к траектории
в сторону движения (рис. 3). По мере
уменьшения Dt путь
Ds все
больше будет приближаться к |Dr|, поэтому
модуль мгновенной скорости
Мгновенная скорость v, таким
образом, есть векторная величина, равная
первой производной радиуса-вектора
движущейся точки по времени. Так как
секущая в пределе совпадает с
касательной, то вектор скорости v
направлен по касательной к траектории
в сторону движения (рис. 3). По мере
уменьшения Dt путь
Ds все
больше будет приближаться к |Dr|, поэтому
модуль мгновенной скорости
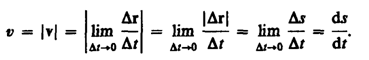 Таким
образом, модуль мгновенной скорости
равен первой производной пути по
времени:
Таким
образом, модуль мгновенной скорости
равен первой производной пути по
времени:
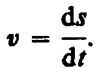 (2.2)
(2.2)
При неравномерном
движении — модуль
мгновенной скорости с течением времени
изменяется. В данном случае пользуются
скалярной величиной ávñ
— средней
скоростьюнеравномерного
движения:
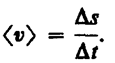 Из
рис. 3 вытекает, что ávñ>
|ávñ|, так как Ds >
|Dr|, и только в случае прямолинейного
движения
Из
рис. 3 вытекает, что ávñ>
|ávñ|, так как Ds >
|Dr|, и только в случае прямолинейного
движения
![]() Если
выражение ds = vdt(см.
формулу (2.2)) проинтегрировать по времени
в пределах от t до t+
Dt,
то найдем длину пути, пройденного точкой
за время Dt:
Если
выражение ds = vdt(см.
формулу (2.2)) проинтегрировать по времени
в пределах от t до t+
Dt,
то найдем длину пути, пройденного точкой
за время Dt:
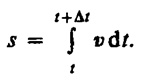 (2.3)
В
случае равномерного
движения числовое
значение мгновенной скорости постоянно;
тогда выражение (2.3) примет вид
(2.3)
В
случае равномерного
движения числовое
значение мгновенной скорости постоянно;
тогда выражение (2.3) примет вид
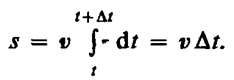 Длина
пути, пройденного точкой за промежуток
времени от t1
до t2,
дается интегралом
Длина
пути, пройденного точкой за промежуток
времени от t1
до t2,
дается интегралом
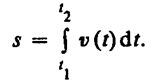

Ускорение
и его составляющие
В случае неравномерного движения
важно знать, как быстро изменяется
скорость с течением времени. Физической
величиной, характеризующей быстроту
изменения скорости по модулю и направлению,
является ускорение
Рассмотрим плоское
движение, т.е.
движение, при котором все участки
траектории точки лежат в одной плоскости.
Пусть вектор v задает скорость точки А в
момент времени t. За
время Dtдвижущаяся
точка перешла в положение В и
приобрела скорость, отличную от v как
по модулю, так и направлению и равную
v1 = v + Dv. Перенесем вектор v1 в точку А и
найдем Dv (рис. 4).

Рис
4
Средним
ускорением неравномерного
движения в интервале от t до t +
Dt называется
векторная величина, равная отношению
изменения скорости Dv к интервалу времени
Dt
![]() Мгновенным
ускорением а
(ускорением) материальной точки в момент
времени t будет
предел среднего ускорения:
Мгновенным
ускорением а
(ускорением) материальной точки в момент
времени t будет
предел среднего ускорения:
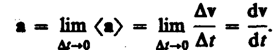 Таким
образом, ускорение a есть векторная
величина, равная первой производной
скорости по времени.
Тангенциальная
составляющая ускорения
Таким
образом, ускорение a есть векторная
величина, равная первой производной
скорости по времени.
Тангенциальная
составляющая ускорения
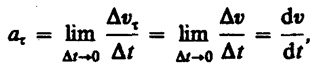 т.
е. равна первой производной по времени
от модуля скорости, определяя тем самым
быстроту изменения скорости по модулю.
Найдем вторую составляющую
ускорения. Допустим, что точка В достаточно
близка к точке А, поэтому
Ds можно
считать дугой окружности некоторого
радиуса r, мало отличающейся от
хорды АВ. Тогда
из подобия треугольников АОВ и EADследует
Dvn/AB=
v1/r, но так как AB = vDt, то
т.
е. равна первой производной по времени
от модуля скорости, определяя тем самым
быстроту изменения скорости по модулю.
Найдем вторую составляющую
ускорения. Допустим, что точка В достаточно
близка к точке А, поэтому
Ds можно
считать дугой окружности некоторого
радиуса r, мало отличающейся от
хорды АВ. Тогда
из подобия треугольников АОВ и EADследует
Dvn/AB=
v1/r, но так как AB = vDt, то
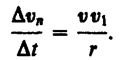 В
пределе при
В
пределе при ![]() получим
получим ![]() .
Поскольку
,
угол EAD стремится
к нулю, а так как треугольник EAD равнобедренный,
то угол ADE между
v и Dvn стремится
к прямому. Следовательно, при
векторы
Dvn и
v оказываются взаимно перпендикулярными.
Tax как вектор скорости направлен по
касательной к траектории, то вектор
Dvn,
перпендикулярный вектору скорости,
направлен к центру ее кривизны. Вторая
составляющая ускорения,
равная
.
Поскольку
,
угол EAD стремится
к нулю, а так как треугольник EAD равнобедренный,
то угол ADE между
v и Dvn стремится
к прямому. Следовательно, при
векторы
Dvn и
v оказываются взаимно перпендикулярными.
Tax как вектор скорости направлен по
касательной к траектории, то вектор
Dvn,
перпендикулярный вектору скорости,
направлен к центру ее кривизны. Вторая
составляющая ускорения,
равная
 называется нормальной
составляющей ускорения и
направлена по нормали к траектории к
центру ее кривизны (поэтому ее называют
также центростремительным
ускорением).
Полное
ускорение тела
есть геометрическая сумма тангенциальной
и нормальной составляющих (рис.5):
называется нормальной
составляющей ускорения и
направлена по нормали к траектории к
центру ее кривизны (поэтому ее называют
также центростремительным
ускорением).
Полное
ускорение тела
есть геометрическая сумма тангенциальной
и нормальной составляющих (рис.5):
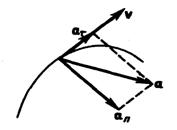 Рис
5
Рис
5
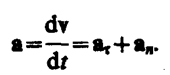 Итак, тангенциальная составляющая
ускорения характеризует быстроту
изменения скорости по модулю (направлена
по касательной к траектории),
а нормальная составляющая
ускорения —быстроту
изменения скорости по направлению (направлена
к центру кривизны траектории).
В
зависимости от тангенциальной и
нормальной составляющих ускорения
движение можно классифицировать
следующим образом:
1)
Итак, тангенциальная составляющая
ускорения характеризует быстроту
изменения скорости по модулю (направлена
по касательной к траектории),
а нормальная составляющая
ускорения —быстроту
изменения скорости по направлению (направлена
к центру кривизны траектории).
В
зависимости от тангенциальной и
нормальной составляющих ускорения
движение можно классифицировать
следующим образом:
1) ![]() , аn= 0 — прямолинейное
равномерное движение;
2)
, аn= 0 — прямолинейное
равномерное движение;
2) ![]() , аn= 0 — прямолинейное
равнопеременное движение. При таком
виде движения
, аn= 0 — прямолинейное
равнопеременное движение. При таком
виде движения
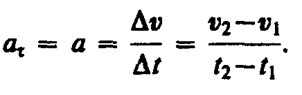 Если
начальный момент времени t1=0,
а начальная скорость v1=v0,
то, обозначив t2=tи v2=v, получим
Если
начальный момент времени t1=0,
а начальная скорость v1=v0,
то, обозначив t2=tи v2=v, получим 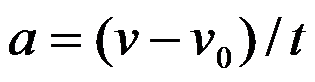 ,
откуда
,
откуда
 Проинтегрировав
эту формулу в пределах от нуля до
произвольного момента времени t, найдем,
что длина пути, пройденного точкой, в
случае равнопеременного движения
Проинтегрировав
эту формулу в пределах от нуля до
произвольного момента времени t, найдем,
что длина пути, пройденного точкой, в
случае равнопеременного движения
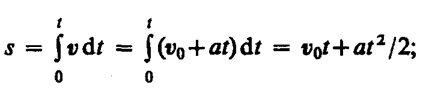 3)
3)![]() , аn= 0—
прямолинейное движение с переменным
ускорением;
4)
, аn= 0—
прямолинейное движение с переменным
ускорением;
4) ![]() , аn= const.
При
скорость
по модулю не изменяется, а изменяется
по направлению. Из формулы an=v2/r следует,
что радиус кривизны должен быть
постоянным. Следовательно, движение
по окружности является
равномерным;
5)
, аn= const.
При
скорость
по модулю не изменяется, а изменяется
по направлению. Из формулы an=v2/r следует,
что радиус кривизны должен быть
постоянным. Следовательно, движение
по окружности является
равномерным;
5)![]() ,
, ![]() — равномерное
криволинейное движение;
6)
— равномерное
криволинейное движение;
6) ![]() ,
—
криволинейное равнопеременное
движение;
7)
,
—
криволинейное равнопеременное
движение;
7) ![]() ,
—
криволинейное движение с переменным
ускорением.
,
—
криволинейное движение с переменным
ускорением.
