7. Свойства вибросигнала роторных агрегатов Представление вибросигнала полигармонической и квазиполигармонической моделями.

В оборудовании, рассматриваемом в настоящей книге, характер взаимодействия элементов подчинен периодическому закону, связанному с вращательным движением. К такого рода агрегатам относятся роторные, где периодическое возбуждение в наиболее простом виде проявляется как сумма гармонических составляющих, кратных основной частоте возмущения, т.е. в виде полигармонической вибрации [2, 5]:

_(7.1)

В роторных агрегатах одной из основных частот возбуждения вибрации является оборотная (роторная) частота, называемая в дальнейшем частотой вращения ротора, которая определяется:

, (7.2)

где – угловая частота вращения ротора.

На установившихся режимах спектр колебаний – дискретный со спектральными составляющими на частоте вращения ротора и ее гармониках (kf_r).

Таким образом, информативными параметрами в такой модели колебаний являются значения амплитуд дискретных составляющих спектра на частоте вращения ротора и ее гармониках и скорость их изменения при увеличении наработки механизма. Амплитуды колебаний на роторных частотах определяются чаще всего величиной дисбаланса, несоосностью валов, кинематическим и погрешностями и отношением, критической частоты вращения ротора к рабочей.

Помимо упомянутой выше вибрации, кратной частоте вращения ротора, в спектре вибросигнала роторного агрегата могут присутствовать такие характерные частотные составляющие, как:

_(7.3)

где z – число элементов взаимодействия на окружности ротора. Для зубчатого зацепления z равно числу зубьев шестерни; для турбины, насоса и вентилятора – числу лопаток на рабочем колесе и т. п.

Модель полигармонического возбуждения колебаний в роторных агрегатах является удобной формой представления спектра колебательного процесса, позволяющего сконцентрировать внимание лишь на определенных частотах (kf_B), кратных основной частоте возбуждения колебаний f_B диагностируемого узла агрегата. Первичный процесс локализации источников повышенной виброактивности конструкции агрегата состоит как раз в выявлении потенциальных источников возбуждения, вызывающих колебания на данной частоте.

Практика вибродиагностики роторных агрегатов показала, что полигармоническая модель вибросигнала является лишь нулевым приближением в описании сложного колебательного процесса реального агрегата, хотя может с успехом использоваться в задачах локализации источников и в задачах диагностирования грубых дефектов типа разрушения лопаток турбины, деталей подшипников, поломки зубьев и т.п., вызывающих существенное увеличение уровня колебаний на определенных частотах. В работе реального агрегата абсолютное повторение с течением времени условий взаимодействия его деталей между собой и с внешней средой практически невозможно.

Погрешности изготовления и монтажа деталей, температурные изменения геометрических параметров деталей и зазоров в сочленениях, изменение вязкости смазки, искажение формы и качества поверхностей взаимодействующих деталей с наработкой, наконец, нестабильность оборотов вала двигателя, вызванная, например, нестабильностью частоты сетевого напряжения, и множество других случайных факторов приводят к флуктуациям амплитуд и размытию дискретных линий спектра полигармонических колебаний.

Более адекватной моделью процесса возбуждения колебаний является суперпозиция узкополосных случайных процессов с кратными средними частотами:

_{, (7.4)}

где kw_r – средняя частота узкополосного процесса, A_k(t) – случайная, медленно меняющаяся огибающая узкополосного процесса, j_k(t) – случайная, медленно меняющаяся фаза, y(t) – уровень шумового возбуждения.

Энергетический спектр такого процесса (рис. 7.1) сосредоточен в узких полосах частот в окрестности kf_r.

При моделировании возбуждения колебаний в роторных агрегатах изменение состояния агрегата можно оценивать по изменению не только величин амплитуд спектральных составляющих, но и уровня шумового возбуждения y(t) с равномерным спектром S_ш(w) в рассматриваемом диапазоне частот. Такая форма представления вибросигнала достаточно хорошо моделирует износ контактирующих поверхностей зубьев колес в редукторе, в подшипниках качения и т.п.

Соотношение энергии периодического и шумового компонентов является информативным параметром вибросигнала, широко используемым при формировании диагностических признаков состояния агрегата.

Импульсная модель акустического сигнала

К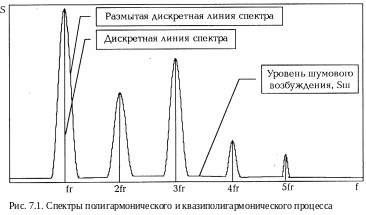 вазиполигармоническая модель колебательного процесса (7.4) мало, что говорит о соотношении амплитуд спектра на частотах kf_r. Эту информацию может дать модель, базирующаяся на представлении процессов возбуждения колебаний в роторных агрегатах в виде периодической последовательности импульсов определенной формы. Такая модель достаточно универсальна, так как она позволяет математически описать процессы возбуждения колебаний как в роторных механизмах типа зубчатого зацепления, подшипников качения и скольжения, турбинах, вентиляторах, циркуляционных и центробежных насосах, так и в поршневых машинах с механизмами циклического ударного действия.

Обозначая функцию, определяющую отдельный импульс, через f(t), можно представить периодическую последовательность импульсов в виде

_, (7.5)

где t_k = kT + t₀ , a k – целое число.

Функция x(t) может быть как детерминированной, так и случайной, отражающей случайность одиночного импульса, которая заключается в том, что его амплитуда, длительность и момент появления могут быть, вообще говоря, случайными величинами.

В ряде практических моделей вибросигнала функционирующих механизмов имеет место периодическая последовательность импульсов, модулированных по амплитуде, при неизменной форме, длительности и частоты следования импульсов. Такой вид модуляции, называемой амплитудно-импульсной модуляцией (АИМ), наиболее часто используется для математического представления акустического сигнала.

Если импульсы, сохраняя свою форму и величину, смещаются во времени на величину Dt, то имеет место временная импульсная модуляция (ВИМ). При этом различают фазово-импульсную модуляцию (ФИМ), когда импульсы имеют постоянную амплитуду и длительность, а меняется их положение на оси времени от периода к периоду, частотно – импульсную модуляцию (ЧИМ), когда импульсы сохраняют амплитуду и положение на оси времени, но меняется их длительность. Все виды модуляции в той или иной мере применимы к задачам моделирования акустического сигнала.

В работающем агрегате в зависимости от характера физического процесса, протекающего в нем, возможны различные отклонения в последовательности импульсов, которые можно охарактеризовать модуляцией амплитуды, длительности или моментов появления импульсов, однако при функционировании оборудования с заданной функцией взаимодействия деталей, определяющейся кинематикой агрегата, наиболее часто встречается амплитудная модуляция, обусловленная разбросом величины силы взаимодействия его элементов в каких-то пределах (неоднородность структуры контактирующих поверхностей зубьев, приводящая к вариации пятна контакта колес зубчатого зацепления; неравномерность воздушного потока в зазоре, отклонение геометрических размеров лопаток турбины вследствие обгара, эрозии и др.). В то же время погрешность окружного шага или явление заедания в зубчатом зацеплении, изгибная деформация, приводящая к неравномерному размещению лопаток в диске или на рабочем колесе турбины, являются причиной возбуждения модулированных по фазе импульсных колебании.

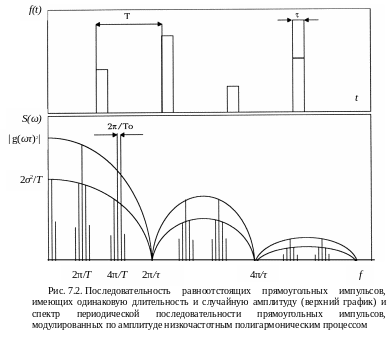
На рис. 7.2 приведен случай периодической последовательности импульсов, следующих с тактовым интервалом Т, равным, например, периоду пересопряжения зубьев в зубчатом зацеплении, модулированных по амплитуде квазидетерминированным процессом. Т_О – период низкочастотного процесса, например оборотов вала шестерни. В нижней части рисунка изображен спектр такого колебательного процесса. В окрестности основных частот 2p/Т_Z следования импульсов в спектре присутствуют комбинационные частоты, отстоящие от основных на q(2p/Т_O), где q – целое число. Амплитуды комбинационных составляющих равны 2s ²_q/Т, где s ²_q – дисперсия компоненты с номером q, s ² – суммарная дисперсия модулирующей функции.

Для формирования диагностического признака используют обычно представление сигнала в достаточно узком диапазоне частот, например, в зоне одной из гармоник основной частоты возбуждения механизма (зубцовой, винтовой, лопаточной и др.).

Колебания представляют в виде модуляции высокочастотного гармонического сигнала суммой гармонических же низкочастотных колебаний.

На рис. 7.3 приведен узкополосный случайный процесс (амплитудная модуляция), описываемый выражением вида

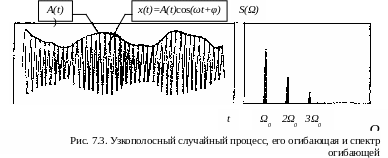
y(t)= A[1+mE(t)]cos(w₀t+j₀), (7.6)

где w₀t – несущая частота, например, частота пересопряжения зубьев, А – амплитуда, m – глубина модуляции (меняется от 0 до 1). E(t) – в общем виде сумма гармонических низкочастотных колебаний кратных основной частоте возбуждения W₀, например, частоте вращения шестерни:

_{. (7.7)}

Выделение огибающей производится с помощью амплитудного детектора.

Дефекты контактирующих поверхностей и характер их проявления в виброакустическом сигнале

Вибродиагностика базируется на анализе изменений свойств вибропроцессов, предполагая, что вибросигнал работающего агрегата содержит всю информацию о взаимодействии его деталей. Задача заключена в разработке алгоритмов извлечения из него информации о состоянии определенного узла и локализации возникающих неисправностей. Большой уровень помех и сравнительно малые изменения полезного сигнала определяют специфику поиска информативных диагностических признаков, чувствительных к развивающемуся дефекту и инвариантных к мешающим факторам. Лишь в исключительных случаях увеличение общего уровня вибросигнала свидетельствует о зарождении определенного дефекта. Как правило, существенное увеличение общего уровня вибрации или отдельных спектральных компонентов говорит лишь о грубых изменениях состояния диагностируемого агрегата, приводящих к потере его работоспособности. Локализация же развивающейся неисправности, еще не приведшей к развитому дефекту, определение степени развития зарождающегося дефекта и прогнозирование возможны лишь на основе исследований тонкой структуры виброакустического сигнала и связи его с кинематикой и динамикой агрегата.

Изучение свойств вибропроцессов роторных агрегатов, показало, что при появлении неисправности меняется структура сигнала, т.е. меняется соотношение между его компонентами или появляются новые. Это подтверждается моделированием колебаний кинематических звеньев механизмов, представляемых в виде суперпозиции квазиполигармонических и шумовых процессов.

Периодическая последовательность импульсов, следующих с частотой пересопряжения зубьев в зубчатых передачах, модулированных по фазе и амплитуде низкочастотным полигармоническим процессом, и шумовой компонент имеют спектр мощности, вида

содержащий:

• спектр низкочастотного и среднечастотного процесса с частотами, кратными оборотной частоте f_r;

• спектр высокочастотного процесса с частотами, кратными зубцовой частоте f_z;

• спектр комбинационных частот mf_z ±k f_r ;

• спектр шумовой компоненты S_N(f).

Аналогичная картина наблюдается при возбуждении колебаний в других механизмах с вращающимися деталями и их узлов, содержащих пару трения, например, турбин, насосов, подшипников качения и скольжения. При появлении неисправностей механизма меняется характер взаимодействия элементов кинематической пары, что приводит к изменению энергетического баланса выражения (7.8).

Характер изменения вибрационных процессов, вызванных изменением состояния контактирующих поверхностей, имеет ряд общих черт, несмотря на различие конструкций и назначение кинематических узлов. Это позволяет сформулировать некоторые правила диагностирования дефектов контактирующих поверхностей типа абразивного износа, выкрашивания и задира, общие для пары зубчатых колес, подшипников скольжения и качения, сопряжения втулка цилиндра – поршень и других узлов, содержащих пару трения.

Истирание (абразивное изнашивание) контактирующих поверхностей сопровождается появлением микронеровностей в зоне контакта, нарушением микро- и макрогеометрии деталей, следствием чего является рост шумовой компоненты S_N(f), увеличение амплитуд гармонического ряда mf_z основной частоты возбуждения кинематического узла и перераспределение амплитуд между гармониками этого ряда.

Выкрашивание (локальное изнашивание) контактирующих поверхностей, проявляющееся в развитии раковин в зоне контакта, вызывает появление периодических всплесков вибросигнала, модулирующих основной процесс возбуждения колебаний.

Периодическое попадание раковин в зону контакта при вращательном движении элементов агрегата (зубчатых колес, тел вращения, сепаратора или обоймы подшипников качения) приводит к появлению в спектре сигнала комбинационных частот mf_z ±k f_r в окрестности основных частот возбуждения, вызванных амплитудной модуляцией. Рост числа выбросов при увеличении их амплитуд, вызванных развитием данного дефекта, приводит к увеличению глубины амплитудной модуляции, росту числа комбинационных частот и перераспределению энергии между ними при неизменности амплитуд основных частот возбуждения.

Развитие трещины в теле детали вращения, приводящее к поломке (зубьев колеса редуктора, сепаратора или обоймы подшипника качения), очень сходно по своему проявлению в спектре сигнала с развитием выкрашивания, но скорость развития данного дефекта значительно выше.

Задир контактирующих поверхностей являющийся следствием увеличения коэффициента демпфирования механической системы, сопровождается мгновенным разогреванием локальных участков, «схватыванием» поверхностей в зоне контакта и последующим наволакиванием металла. Как правило, задир (заедание) развивается при неправильных условиях эксплуатации механизмов: при нарушении условий смазки, при увеличении нагрузки сверх допустимых пределов, при попадании посторонних предметов в зону контакта. Явление задира приводит к нарушению периодичности движения деталей агрегата, к флуктуациям скорости вращения, к появлению выбросов в вибросигнале, к явлению фазовой модуляции К на основных частотах, возбуждения. С развитием задира вибросигнал становится существенно нестационарным из-за нерегулярности выбросов. В спектре сигнала наблюдается падение амплитуд основных частот возбуждения mf_z при одновременном росте амплитуд комбинационных частот (mfz±kfr).

Известно, что отклик механической системы на воздействие кратковременного одиночного импульса, имеющего широкополосный спектр, можно наблюдать на собственных частотах системы, но энергия отклика на каждой из этих частот мала даже при воздействии на систему последовательности импульсов, поэтому данные спектрального анализа колебаний при зарождении и развитии дефектов типа выкрашивания, появления трещин и задира не позволяют с достаточной достоверностью определить вид дефекта. Спектр мощности, являясь усредненной энергетической характеристикой сигнала, годен лишь для распознавания предаварийных ситуаций, находящихся на грани катастрофических изменений в механизме.

Для выявления дефектов на ранней стадии необходимо привлекать более информативные характеристики, такие, например, как число выбросов сигнала в единицу времени, превышающих некоторое пороговое значение, глубина амплитудной и фазовой модуляции, спектр огибающей, кепстр [1, 5–7, 9].

Большинство методов диагностирования зарождающихся дефектов механизмов имеет в своей основе одну и ту же отправную диагностическую модель: развитие дефекта вызывает рост амплитуд и числа кратковременных импульсов в вибросигнале. Задача состоит в применении оптимального способа обработки сигнала, который сводит к минимуму влияние помех и позволяет однозначно соотнести полученную характеристику сигнала с видом дефекта.

Способы выделения информативных компонентов

Характер изменения структуры вибросигнала при выявлении неисправности определяет способ его обработки для выделения информативного компонента, характеризующего изменение технического состояния объекта диагностирования. В зависимости от типа агрегата и вида возникшего в нем дефекта используются различные способы увеличения отношения сигнал/помеха.

Если физика воздействия неисправности на колебания механизма связана с появлением амплитудной или фазовой модуляции, то исследуются свойства огибающей вибросигнала.

Появление в сигнале или усиление периодического компонента заставляют искать эффективный способ выделения периодического сигнала на фоне помехи, например, к методу синхронного накопления.

Появление или усиление полигармонических колебаний можно уловить с помощью кепстрального анализа, сжимающего информацию об изменениях в сигнале до обозримого количества рахмоник, амплитуды которых легко оценить количественно.

Возникновение и развитие дефектов в механизмах приводят к появлению нелинейных эффектов, использование которых для формирования диагностических признаков позволяет получить более ценную диагностическую информацию, чем на основе рассмотрения линейных динамических моделей. Для этой цели используют величины амплитуд комбинационных частот, глубину амплитудной модуляции или частотной девиации.

Перечисленные выше методы анализа виброакустических процессов позволяют сформировать характерные диагностические признаки зарождающихся дефектов даже в тех случаях, когда спектр мощности сигнала практически не меняется. При наличии инвариантности диагностических признаков гарантируется достоверность диагностирования даже на ранней стадии развития дефекта.