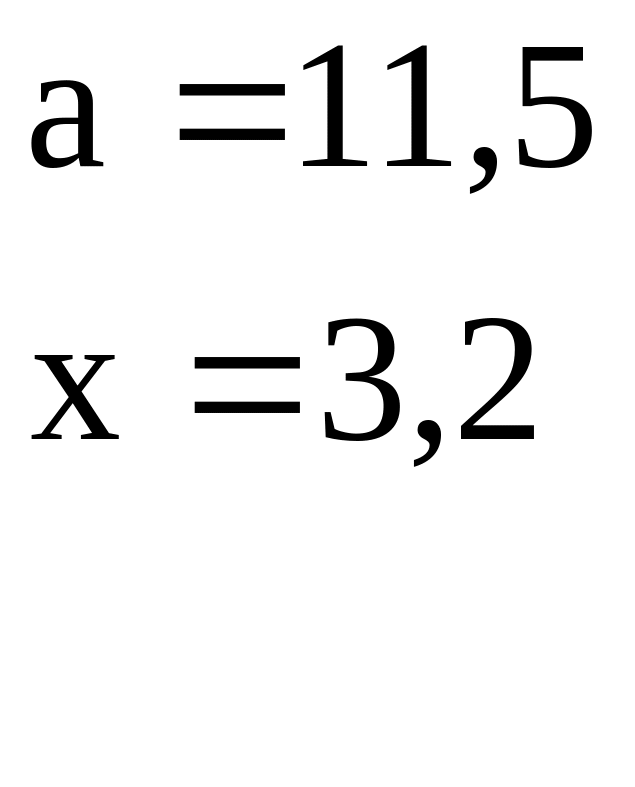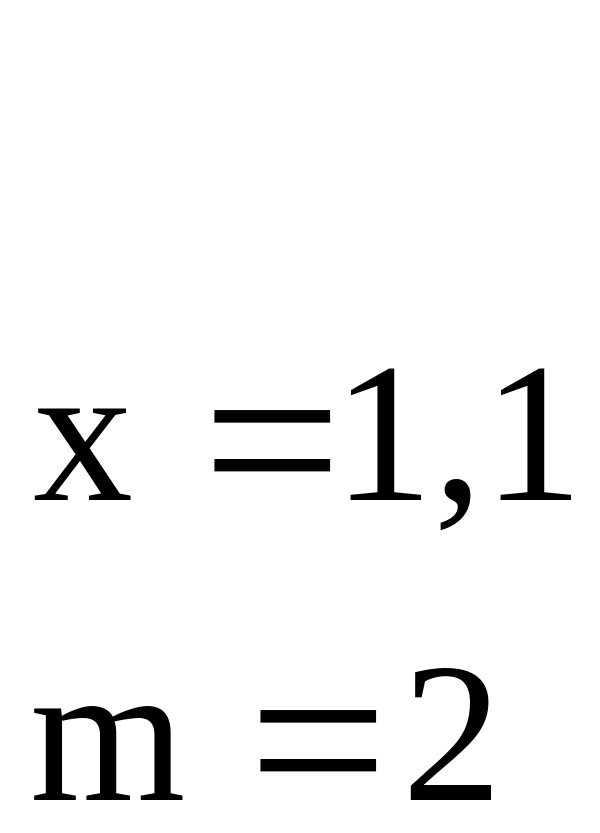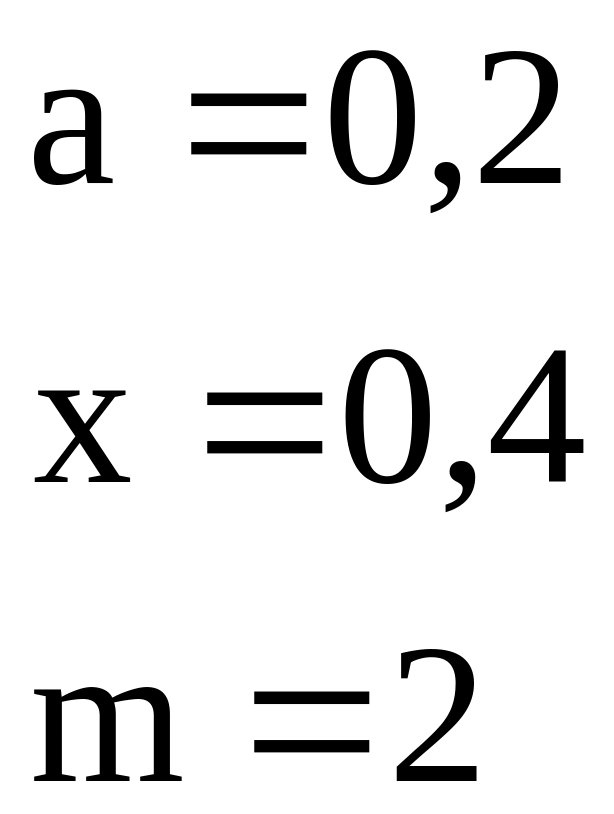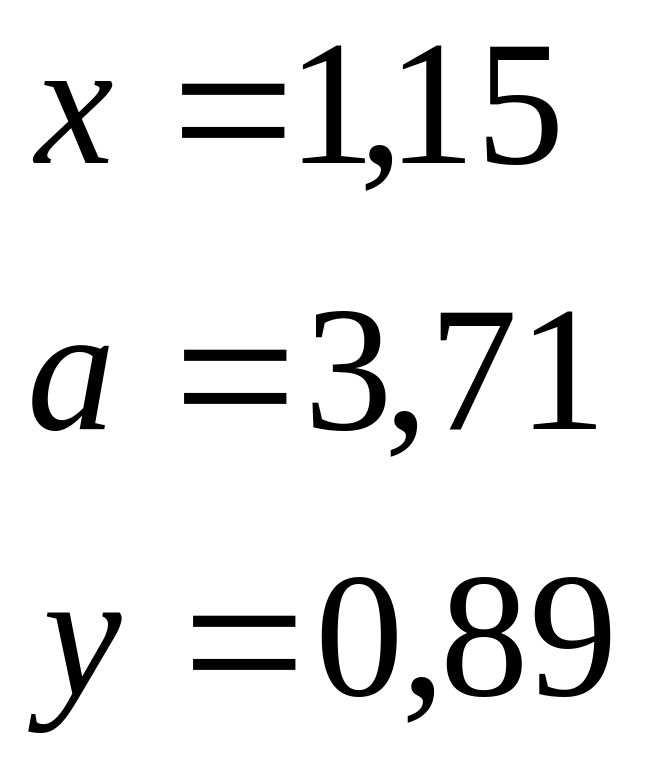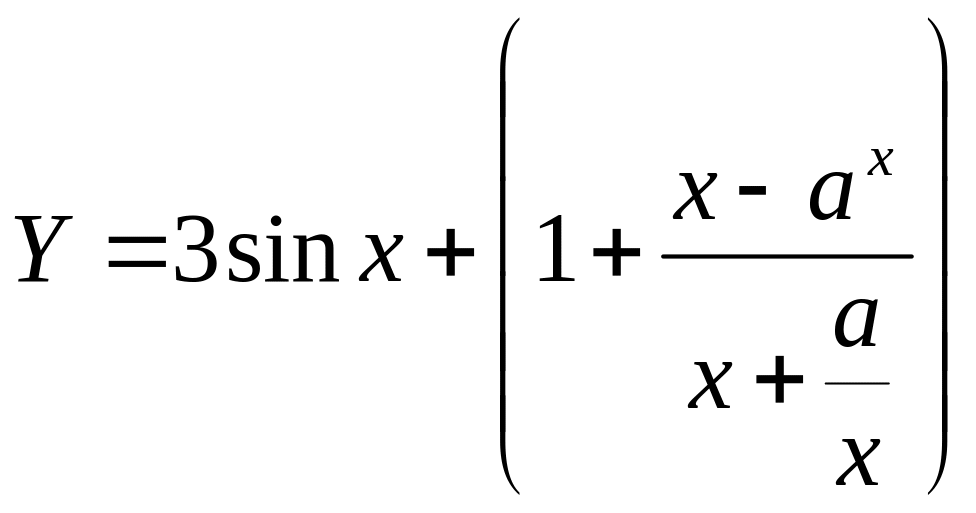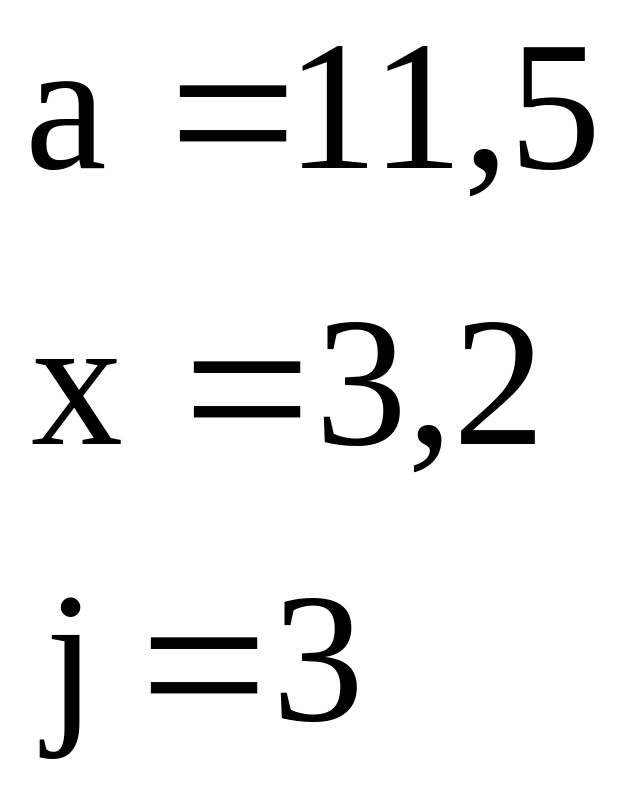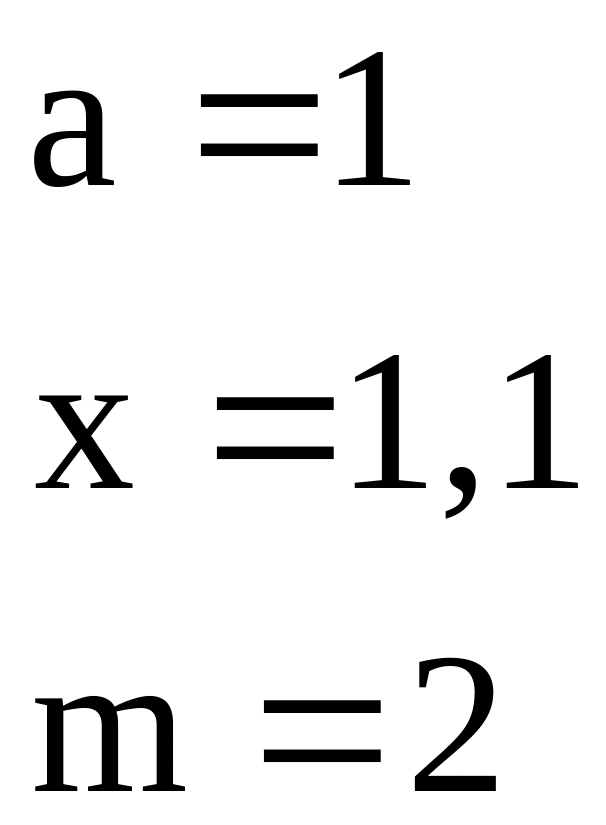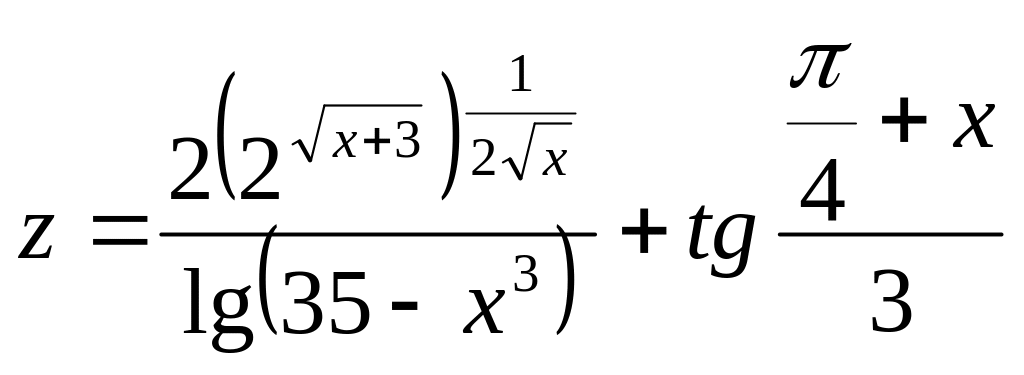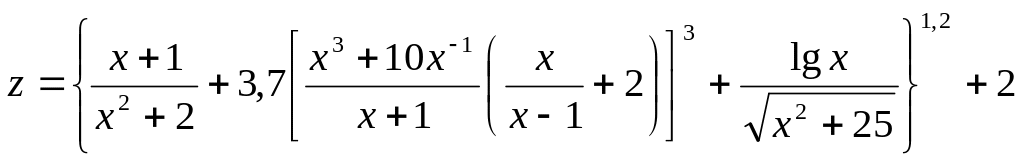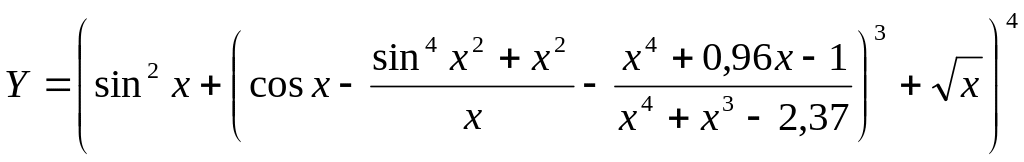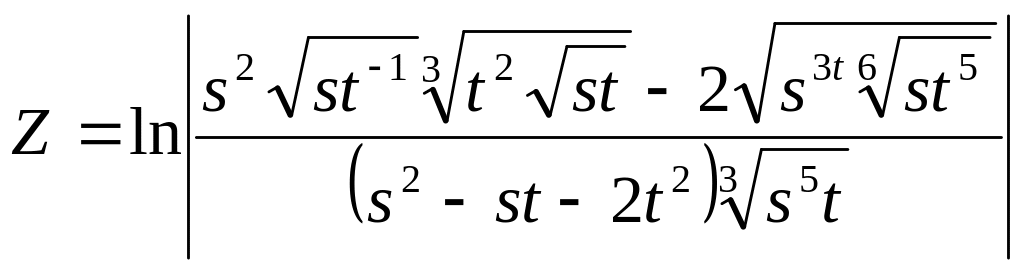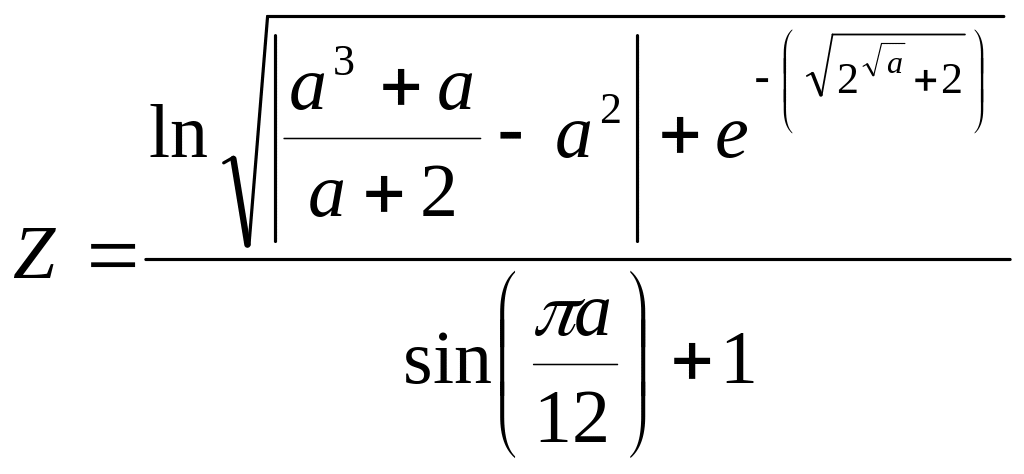Задание №1
Учитывая значения переменных, вычислить арифметическое выаржение по формуле согласно варианта. Алгоритм решения задачи представить в виде блок-схемы.
Таблица 1
вар.№ |
Формула для вычисления |
Переменные |
вар.№ |
Формула для вычисления |
Переменные |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
|
|
11 |
|
|
2 |
|
|
12 |
|
|
3 |
|
|
13 |
|
|
4 |
|
|
14 |
|
|
5 |
|
|
15 |
|
|
6 |
|
|
16 |
|
|
7 |
|
|
17 |
|
|
8 |
|
|
18 |
|
|
9 |
|
|
19 |
|
|
10 |
|
|
20 |
|
|
Задание №2
Учитывая значения переменных, вычислить арифметическое выаржение по формуле согласно варианта. Алгоритм решения задачи представить в виде блок-схемы.
Таблица 2
вар.№ |
Формула для вычисления |
Переменные |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
Задание №3
Учитывая предел изменения значения переменных, вычислить функцию по формуле согласно варианта. Алгоритм решения задачи представить в виде блок-схемы.
Таблица 3
Вариант № |
Расчетная формула |
Условие |
Границы и шаг изменения переменных |
Ва риант № |
Расчетная формула |
Условие |
Границы и шаг изменения переменных |
1 |
|
1<=t<=2 t<1 t>2 |
t[0;3]; ∆t=0,15; |
11 |
|
x<2,8 2,8<=x<6 x>=6 |
x[0;7]; ∆x=0,15 |
2 |
|
x<1,3 x=1,3 x>1,3 |
x[0;2]; x=0,2 |
12 |
|
x>1 x<=1 |
x[0;2]; x=0,1 |
3 |
|
x<1,2 x=1,2 x.1,2 |
x[1;2]; x=0,05 |
13 |
|
i<4 4<=i<=6 i>6 |
i[0;12]; i=1 |
4 |
|
x<1,4 x=1,4 x.1,4 |
x[0,7;2];x=0,1 |
14 |
|
((i2+1)/n)>0
((i2+1)/n)<0 |
i[1;10]; i=1 |
5 |
|
x<1 x=1 x>2 |
x[0,5;3]; x=0,2 |
15 |
|
t<0,1 t=0,1 t>0,1 |
t[-1;1]; t=0,2 |
6 |
|
x>a x=a x<a
|
x[1;5]; x=0,5 |
16 |
|
x>3,5 x<=3,5 |
x[2;5]; x=0,2 |
7 |
|
bx<1 bx=1 bx>1 |
x[0,1;1];x=0,1 |
17 |
|
x>a x=a x<a |
x[1;5]; x=0,25 |
8 |
|
x>2,5 x<=2,5 |
x[2;5]; x=0,25 |
18 |
|
x>a x=a x<a |
x[0;5]; x=0,25 |
9 |
|
x>1 x<=1 |
x[0,5;2]; x=0,1 |
19 |
|
x>a x=a x<a |
x[0;3]; x=0,2 |
10 |
|
x<0,5 x=0,5 x>0,5 |
x[0,2;2]; x=0,1 |
20 |
|
x<0,5 x=0,5 x>0,5 |
x[0;2]; x=0,05 |