
- •1 Механика
- •1.1 Основные понятия, законы и формулы
- •1.2 Примеры решения задач
- •Решение
- •Решение
- •Решение.
- •1.3 Задачи для самостоятельного решения
- •2. Молекулярная физика и термодинамика
- •2.1. Постоянные величины
- •2.2.Основные обозначения
- •2.3. Основные понятия, законы и формулы
- •Относительные атомные массы а (округленные значения) некоторых химических элементов
- •2.3 Примеры решения задач
- •Решение
- •Решение.
- •Решение.
- •Решение
- •Решение
- •Решение.
- •Решение
- •2.4 Задачи для самостоятельного решения
- •3. Электростатика. Постоянный ток.
- •3.1 Основные понятия и формулы.
- •Решение.
- •Решение
- •Решение
- •Решение
- •3.3.Методические указания к решению задач.
- •3.4. Задачи для самостоятельного решения
- •4. Магнетизм
- •4.1 Основные понятия и формулы
- •4.2 Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •4.3 Задачи для самостоятельного решения
- •5 Оптика
- •5.1 Основные понятия и формулы
- •5 .2 Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •5.3 Задачи для самостоятельного решения
- •6 Физика микромира
- •6.1 Основные понятия и формулы
- •6.2 Справочные таблицы
- •Основные физические постоянные
- •Масса и энергия покоя некоторых частиц
- •Периоды полураспада радиоактивных изотопов
- •Массы атомов легких изотопов
- •6.3 Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •6.4 Задачи для самостоятельного решения
- •Список использованной литературы
- •1.Учебники.
- •2.Сборники задач.
- •Приложения
- •1.Порядок выбора варианта и требования к оформлению контрольной работы.
- •Определение варианта по шифру
- •2.Таблицы заданий на контрольные работы по вариантам бакалавриат
- •Специалисты
- •Специальности поз, позс
- •Специальности пгсз, пгсзс
- •Содержание
Решение
Коэффициент теплопроводности воздуха определяется формулой
= . (2.1.)
Величины
=
и
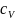 =
=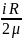 от давления не зависят.
от давления не зависят.
Плотность воздуха, как следует из уравнения Менделеева-Клапейрона:
=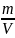 =
=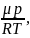
прямо пропорциональна давлению и при откачке будет уменьшаться. Средняя длина свободного пробега молекул
=
=
=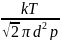
обратно
пропорциональна давлению и при откачке
будет увеличиваться. Произведение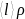 ,
а
следовательно, и коэффициент
теплопроводности
некоторое
время, несмотря на откачку воздуха,
будут оставаться
постоянными.
,
а
следовательно, и коэффициент
теплопроводности
некоторое
время, несмотря на откачку воздуха,
будут оставаться
постоянными.
Однако, начиная с некоторого значения давления p', при котором средняя длина свободного пробега молекул, обусловленная их соударением друг с другом, станет равной расстоянию между стенками термоса
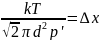 (2.2)
(2.2)
коэффициент теплопроводности начнет уменьшаться. Начиная с этого момента, молекулы будут летать между стенками термоса, практически не испытывая столкновений друг с другом. Величина при этом будет определяться формулой,
аналогичной (2.1.), но с заменой на :
=
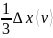 .
.
и, за счет уменьшения плотности газа при дальнейшей откачке, будет уменьшаться.
Находим давление р' из соотношения (2.2.):
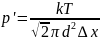
Подставляя числовые данные, получаем
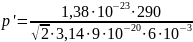 =
=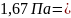 1,25
1,25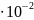 мм.рт.ст.
мм.рт.ст.
Пример 6 .
Кислород
массой т
=1
кг
занимает объем V1
=
1м3
и находится под
давлением р1
= 0,2 МПа.
Газ был нагрет сначала при постоянном
давлении до объема V2=3
м3,
а затем при постоянном объеме до давления
р3
=
0,5 МПа . Найти изменение внутренней
энергии газа
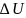 ,
совершенную
им работу А
и
теплоту Q,
пере
,
совершенную
им работу А
и
теплоту Q,
пере
р, МПа данную газу. Построить график процесса.
Р3
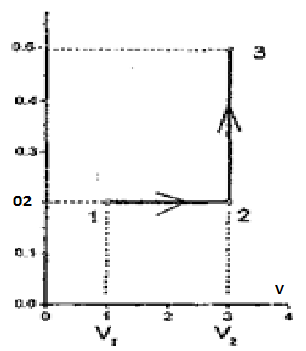 Дано:
т = 2 кг;
V1
= 1m3;
p1
= р2 =
0,2
106
Па;
Дано:
т = 2 кг;
V1
= 1m3;
p1
= р2 =
0,2
106
Па;
V2= V3= 3 м3; Рз=0,5 10б Па.
Найти:
 A;
Q.
A;
Q.
Решение.
р1
Р1
 внутренней
энергии газа
внутренней
энергии газа
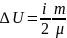 R(T1
– Т2
),
R(T1
– Т2
),
где i = 5 - число степеней свободы молекулы
кислорода (двухатомная молекула имеет 5 степеней
Рис.2.1 свободы), T1 и T3 - температуры газа в начальном (первом) и конечном(третьем) состояниях. Применяя к первому и третьему состояниям уравнения Менделеева-Клапейрона
рр
p
p1
p
p1
p
p1


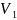 =
R
=
R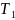 ;
p2
;
p2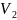 =
R
=
R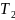
получаем: = (p3V3 – р2V2),
Полная работа, совершенная газом, равна работе при изобарном процессе:
А = p1(V2 – V1) ;
так как работа при изохорном процессе равна нулю.
В соответствии первому закону термодинамики теплота Q, полученная газом, равна
Q = + A.
Выполняем вычисления:
=
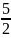 (0,5
106
3-
0,2
106
(0,5
106
3-
0,2
106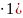 = 3,25
106Дж
= 3,25МДж;
= 3,25
106Дж
= 3,25МДж;
А = 0,2 106(3-1) = 0,4 106 Дж = 0,4МДж;
Q = 3,25 + 0,4 = 3,65 МДж.
Пример7
В цилиндре под поршнем находится водород массой т = 0,02 кг при температуре T1 = 300К. Водород сначала расширился адиабатно, увеличив свой объем в п1 = 5 раз, а затем был сжат изотермически, причем объем газа уменьшился в п2 =5 раз. Найти температуру Т2 в конце адиабатного расширения и работу, совершенную газом при этих процессах. Построить график процесса.
Дано:
т
= 0,02
кг; Т1
=300 К; п1
=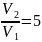 п2 =
п2 =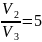 .
.
Найти: Т2; А12; А23.
 р
Решение
р
Решение

 График процесса
изображен на рис. 2.2
График процесса
изображен на рис. 2.2
 1
Температура
и объем газа первого и
1
Температура
и объем газа первого и
второго состояний связаны между собой
адиабата уравнением Пуассона
3 Т2 = Тl



Температура в конце адиабатного расширения определяется формулой
изотерма
2
=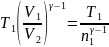 .
.
0 V
Рис. 2.2 Коэффициент Пуассона для водорода
как двухатомного газа (i = 5) равен
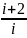 =
=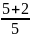 = 1,4
= 1,4
Работа водорода при адиабатном расширении может быть найдена по формуле
А1,2 = R(T1 – Т2 ),
Работа газа при изотермическом сжатии отрицательна и равна
А2,3=
R
ln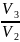 =
=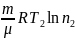
Производим вычисления, с учетом того, что молярная масса водорода
= 2 10-3 кг/моль.
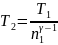 =
=
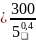 =157К
А1,2 =
=157К
А1,2 =
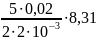 (300
– 157 )
=29,8
(300
– 157 )
=29,8 Дж=29,8кДж
Дж=29,8кДж
А2,3
=
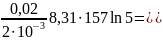 -
21
103
Дж = - 21 кДж.
-
21
103
Дж = - 21 кДж.
Пример 8.
Тепловая машина работает по обратимому циклу Карно. Температура нагревателя Т1 = 500К.Определить КПД цикла и температуру Т2
холодильника, если за счет каждого килоджоуля теплоты Q1, полученной от нагревателя, машина совершает работу А = 350 Дж.
Дано: Т1 = 500 К; Q1=1000 Дж; А = 350 Дж.
Найти: ; Т2.
