
- •1 Механика
- •1.1 Основные понятия, законы и формулы
- •1.2 Примеры решения задач
- •Решение
- •Решение
- •Решение.
- •1.3 Задачи для самостоятельного решения
- •2. Молекулярная физика и термодинамика
- •2.1. Постоянные величины
- •2.2.Основные обозначения
- •2.3. Основные понятия, законы и формулы
- •Относительные атомные массы а (округленные значения) некоторых химических элементов
- •2.3 Примеры решения задач
- •Решение
- •Решение.
- •Решение.
- •Решение
- •Решение
- •Решение.
- •Решение
- •2.4 Задачи для самостоятельного решения
- •3. Электростатика. Постоянный ток.
- •3.1 Основные понятия и формулы.
- •Решение.
- •Решение
- •Решение
- •Решение
- •3.3.Методические указания к решению задач.
- •3.4. Задачи для самостоятельного решения
- •4. Магнетизм
- •4.1 Основные понятия и формулы
- •4.2 Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •4.3 Задачи для самостоятельного решения
- •5 Оптика
- •5.1 Основные понятия и формулы
- •5 .2 Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •5.3 Задачи для самостоятельного решения
- •6 Физика микромира
- •6.1 Основные понятия и формулы
- •6.2 Справочные таблицы
- •Основные физические постоянные
- •Масса и энергия покоя некоторых частиц
- •Периоды полураспада радиоактивных изотопов
- •Массы атомов легких изотопов
- •6.3 Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •6.4 Задачи для самостоятельного решения
- •Список использованной литературы
- •1.Учебники.
- •2.Сборники задач.
- •Приложения
- •1.Порядок выбора варианта и требования к оформлению контрольной работы.
- •Определение варианта по шифру
- •2.Таблицы заданий на контрольные работы по вариантам бакалавриат
- •Специалисты
- •Специальности поз, позс
- •Специальности пгсз, пгсзс
- •Содержание
Решение.
Учитывая, что сумма моментов всех внешних сил, действующих на систему человек - платформа, равна нулю, запишем закон сохранения момента импульса:
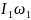 =
=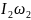 (5)
(5)
где
I1
=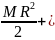 mR2
- момент
инерции системы, когда человек стоит
на
mR2
- момент
инерции системы, когда человек стоит
на
краю платформы (человека считаем материальной точкой, а платформу -однородным диском);
12
=
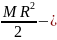 момент
инерции системы, когда человек находится
в
центре платформы.
момент
инерции системы, когда человек находится
в
центре платформы.
Подставляя I1 и I2 в (5), получаем:
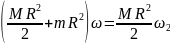
Откуда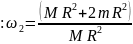 .
.
Работа, совершаемая человеком, равна изменению кинетической
энергии
системы: А
=
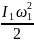 -
-
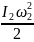 .
.
Пример 7
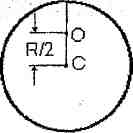
Диск радиуса R совершает колебания вокруг оси, проходящей через середину его радиуса перпендикулярно плоскости диска (рис.1. 6). Определить период колебаний диска.
 Решение
Решение
Применим формулу для определения
Т
= 2
.
Рис.1. 6
где: m - масса диска
d = R/2 – удаление центра тяжести диска от точки вращения, что видно из рис. 6.
I - момент инерции диска относительно точки "О". Его рассчитываем по теореме Штейнера:
I =
+
md2
=
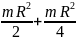 =
=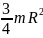 .
.
Окончательно
получаем: T=
2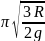
![]()
1.3 Задачи для самостоятельного решения
1.001 -1.022 Кинематика.
1.023-1.051 Динамика материальной точки.
1.052 -1.085 Импульс, работа, энергия.
1.086-1.101 Момент инерции. Теорема Штейнера.
1.102-1.125 Динамика твёрдого тела.
1.126-1.137 Момент количества движения.
1.138-1.154 Колебания.
1.001. Зависимость перемещения прямолинейно движущегося тела от времени имеет вид: s = At – Bt2 + Ct3 , где А=1 м/с, В = 2 м/с2 и С = 0,5 м/с3. Найти расстояние, пройденное телом, скорость движения v и ускорение а тела через время t = 2 с после начала движения. Построить график зависимости ускорения а от времени t.
1.002. Зависимость координаты тела от времени дается уравнением:
х = А - Bt + Ct2, где А = 6 м, В =4 м/с и С = 1м/с2. Найти cреднее ускорение а тела для интервала времени 0 < t < 4с. Построить график зависимости скорости v от времени t для интервала 0 < t < 5 с и найти среднюю скорость в этом интервале времени.
1.003. Зависимость координаты тела от времени дается уравнением:
х =А +
Bt
+ Ct3\,
где А
= 3 м, В
= 2 м/с и С =
1 м/с2.
С какой средней скоростью
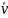 двигалось
тело в течение второй секунды движения?
двигалось
тело в течение второй секунды движения?
1.004. Зависимость координаты тела от времени дастся уравнением:
х =A
+ Bt
+ Ct2
+ Dt3
,где С
= 0,14 м/с2
и D
= 0,01 м/с3.
Через какое время t
после начала
движения тело будет иметь ускорение
а=1
м/с2?
Каково среднее ускорение тела
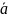 в
этом промежутке времени?
в
этом промежутке времени?
1.005. Камень брошен горизонтально со скоростью v0 = 15 м/с. Найти нормальное и тангенциальное ускорения камня через время t = 1 с после начала движения. Сопротивлением воздуха пренебречь.
1.006. Камень брошен горизонтально со скоростью v0 =10 м/с. Найти радиус кривизны R траектории камня через время t = 1 с после начала движения. Сопротивлением воздуха пренебречь.
1.007. Тело брошено со скоростью v0 = 10 м/с под углом = 45° к горизонту. Найти радиус кривизны R траектории тела в верхней точке траектории. Сопротивлением воздуха пренебречь.
1.008.Ось с двумя дисками, расположенными на расстоянии l = 0,5 м друг от друга, вращается с частотой п =1600 об/мин. Пуля, летящая вдоль оси, пробивает оба диска, причем отверстие от пули во втором диске смещено относительно отверстия в первом диске на угол = 12°. Найти скорость v пули.
1.009. Найти радиус R вращающегося колеса, если известно, что линейная скорость v1 точки, лежащей на ободе, в 2,5 раза больше линейной скорости v2 точки, находящейся на 6 см ближе к оси колеса.
1.010.Колесо, вращающееся с постоянным угловым ускорением, достигло угловой скорости = 20 рад/с, совершив 10 оборотов от начала вращения. Найти угловое ускорение колеса.
1.011.Колесо, вращаясь с постоянным угловым ускорением, через одну минуту после начала вращения приобретает частоту п = 720 об/мин. Найти угловое ускорение и количество оборотов N колеса за это время.
1.012.Точка движется по окружности радиусом R = 20 см с постоянным тангенциальным ускорением = 10 см/с2. Через какое время t после начала движения нормальное ускорение аn точки будет вдвое больше тангенциального?
1.013. Точка движется
по окружности радиусом R
= 10 см с
постоянным тангенциальным
ускорением
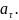 Найти тангенциальное
ускорение
точки, если известно, что к концу пятого
оборота после начала движения линейная
скорость точки достигла значения v=
79,2 см/с.
Найти тангенциальное
ускорение
точки, если известно, что к концу пятого
оборота после начала движения линейная
скорость точки достигла значения v=
79,2 см/с.
1.014.Точка движется по окружности радиусом R =10 см с постоянным тангенциальным ускорением . Найти нормальное ускорение аn точки через время t = 20 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки равна v= 10 см/с.
1.015. Колесо радиусом R = 10 см вращается с постоянным угловым ускорением =2 рад/с2. Найти величину и направление полного ускорения точек на ободе колеса к концу первой секунды после начала движения.
1.016.Точка движется по окружности радиусом R = 2 см. Зависимость пути от времени описывается уравнением s = Ct3, где С = 0,1 см/с3. Найти нормальное ап и тангенциальное ускорение точки в момент, когда линейная скорость точки v= 0,3 см/с.
1.017.Точка движется по окружности так, что зависимость от времени криволинейной координаты точки, отсчитываемой вдоль окружности, имеет вид: s = A - Bt + Ct2, где В = 2 м/с и С = 1 м/с2. Найти полное а ускорение точки через время t = 3 с после начала движения, если известно, что в момент времени t=2 с нормальное ускорение точки равно 0,5 м/с2.
1.018.Колесо вращается с постоянным угловым ускорением =2 рад/с2. Через время t= 0,5 с после начала движения полное ускорение колеса а = =1,36 см/с2. Найти радиус R колеса.
1.019. Колесо радиусом R = 0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением = А + Bt + Ct3, где B = 2 рад/с и С = 1 рад/с3. Для точек, лежащих на ободе колеса, найти через время t = 2 с после начала движения: а) угловую скорость , б) линейную скорость v; в) угловое ускорение ; д) тангенциальное , и нормальное аn ускорения.
1.020. Диск радиусом R = 5 см вращается так, что зависимость от времени угла поворота радиуса диска имеет вид: = А + Bt + Сt2 + Dt3, где D = 1 рад/с3. Для точек, лежащих на ободе диска, найти изменение тангенциального ускорения за одну секунду.
1.021.Колесо радиусом R = 10 см вращается так, что зависимость от времени линейной скорости точек, лежащих на ободе колеса, задается уравнением v = At + Bt3, где А = 3 см/с2 и В = 1 см/с3. Найти угол , который составляет вектор полного ускорения с радиусом колеса в момент времени t=4с после начала движения.
1.022.Колесо вращается так, что зависимость угла поворота радиуса колеса от времени описывается уравнением = А + Bt + Ct3, где В=1рад/с, С = 1 рад/с2 и D = 1рад/с3. Найти радиус R колеса, если известно, что к концу второй секунды движения нормальное ускорение точек, лежащих на ободе колеса, равно 57,8 м/с2. Какова линейная скорость точек обода колеса в этот момент времени?
1.023.К нити подвешена гиря. Если поднимать гирю с ускорением а=2 м/с2, то сила натяжения нити Т1 будет вдвое меньше силы натяжения Т2, при которой нить разрывается. С каким максимальным ускорением а2 можно поднимать гирю, чтобы нить не разорвалась?
1.024. На тросе массой m1=3 кг и длиной 1,5 м поднимают груз массой
т = 67 кг вертикально вверх, прикладывая к тросу в верхней точке силу F=770 Н. Определить силу натяжения троса в сечении, находящемся на расстоянии 50 см от точки крепления троса к грузу. Сопротивлением воздуха пренебречь.
1.025. К концам горизонтально расположенного однородного стержня
массой 6 кг приложены две противоположно направленные силы F1 = 3 Н и
F2 = 7 Н, действующие вдоль стержня. Определить силу
натяжения стержня
в поперечном сечении, находящемся от
точки
приложения
второй силы на расстоянии, равном
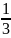 длины стержня.
длины стержня.

 1.026.
На горизонтальной плоской поверхности
1.026.
На горизонтальной плоской поверхности
расположены два соприкасающихся бруска массами

 т1
= 2 кг и т2
= 3 кг. Ко
второму бруску приложена
m1
m2
т1
= 2 кг и т2
= 3 кг. Ко
второму бруску приложена
m1
m2
горизонтально
направленная сила F
= 10Н (см.рис).
Рис. к задаче 1.026 С какой силой
бруски действуют друг на друга, если
коэффициенты трения брусков о поверхность
соответственно равны
 0,1
и
0,1
и
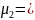 0,2
?
0,2
?
1.027.Тело массой т = 0,5 кг движется прямолинейно, и зависимость координаты тела от времени имеет вид: х =А - Bt + Ct2 - Dt3, где С = 5 м/с2 и D = 1 м/с3. Найти силу F, действующую на тело в конце первой секунды движения.
1.028.Под действием силы F= 10 Н тело движется прямолинейно, и зависимость координаты тела от времени описывается уравнением:
х =A - Bt+ Ct2, где С = 1 м/с2. Найти массу т тела.
1.029.
Тело массой т
= 0,6 кг
движется прямолинейно так, что
зависимость
координаты тела от времени задается
уравнением: х
= Asin
t,
где А
= 5 см и
=
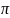 рад/с.
Найти силу F,
действующую
на тело через время t=
рад/с.
Найти силу F,
действующую
на тело через время t=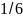 с
после начала движения.
с
после начала движения.
1.030. Трамвай, трогаясь с места, движется с ускорением а = 0,5 м/с2. Через время t = 12 с после начала движения мотор выключается и трамвай движется до остановки равнозамедленно. Коэффициент трения на всем пути = 0,01. Найти время движения трамвая и расстояние, пройденное трамваем за время движения.
1.031.На автомобиль массой т = 1 т во время движения действует сила трения Fтр, составляющая 10 % от действующей на автомобиль силы тяжести. Какова должна быть сила тяги F, действующая на автомобиль, чтобы он двигался: а) равномерно; б) с постоянным ускорением а = 2 м/с2?
1.032. Какой угол
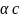 горизонтом
составляет поверхность бензина в баке
автомобиля, движущегося с ускорением
а =
1 м/с2 ?
горизонтом
составляет поверхность бензина в баке
автомобиля, движущегося с ускорением
а =
1 м/с2 ?
1.033. Шар на нити подвешен к потолку трамвайного вагона. Вагон останавливается, и его скорость за 3с равномерно уменьшается от v1 = 18 км/ч до
v2 = 6 км/ч. На какой угол от вертикали отклонится при этом нить с шаром?
1.034. При торможении вагона его скорость за время t = 3,3 с равномерно уменьшается от v1= 47,5 км/ч до v2 = 30 км/ч. При каком предельном значении коэффициента трения между чемоданом и полкой чемодан при торможении начнет скользить по полке?
1.035. Тело лежит на наклонной плоскости, составляющей с горизонтом угол = 4°. При каком предельном значении коэффициента трения тела о плоскость оно начнет скользить по наклонной плоскости? С каким ускорением
будет скользить тело по плоскости, если коэффициент трения = 0,03?
1.036.Тело скользит вниз по наклонной плоскости, составляющей с горизонтом угол = 45°. Зависимость от времени пути, пройденного телом, имеет вид: s = At2, где А 2,1 м/с2. Найти коэффициент трения тела о плоскость.
1.037.Тело массой 200 г тянут вверх по наклонной плоскости, прикладывая силу F= 1,7 Н, направленную вдоль наклонной плоскости. При каком коэффициенте трения между телом и плоскостью движение будет равномерным? Угол наклона плоскости к горизонту равен 30°.
1.038. За какое время тело соскользнет с наклонной плоскости высотой
h
= 10 м и углом
наклона к горизонту
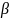 = 60°, если по наклонной плоскости с углом
наклона а
= 30° при
таком
же
коэффициенте трения это тело движется
равномерно?
= 60°, если по наклонной плоскости с углом
наклона а
= 30° при
таком
же
коэффициенте трения это тело движется
равномерно?





 l
l


 1.039.
Внутри ящика находится куб массой
a
1.039.
Внутри ящика находится куб массой
a
т = 2 кг с длиной ребра l = 20см, который H


 опирается
на три опоры (см. рис).Определить
силы,
опирается
на три опоры (см. рис).Определить
силы,
действующие на куб со стороны опор, если ящик
движется с горизонтальным ускорением а =2 м/с2. Рис. к задаче 1.039
Расстояние верхней опоры от нижней грани куба Н = 15 см.
1.040. Конькобежец, движущийся со скоростью v = 4 м/с, делает поворот радиусом R = 10 м. Почему и на какой угол от вертикали он отклоняется?
1.041.По горизонтальным рельсам, уложенным по кругу радиусом R = 300 м, катится вагон. С какой максимальной скоростью может двигаться вагон, если его центр тяжести находится на высоте Н=1,5 м, а расстояние между рельсами l = 1 м. Учесть, что колеса вагона имеют реборды.
1.042.Самолет, летящий со скоростью v= 900 км/ч, делает «мертвую петлю». Каким должен быть радиус «мертвой петли» R, чтобы наибольшая сила F, прижимающая летчика к сидению, была равна шестикратной силе тяжести, действующей на летчика?
1.043. Мотоциклист едет по горизонтальной дороге со скоростью v=72 км/ч, делая поворот радиусом R = 100 м. На какой угол а от вертикали он должен при этом отклониться, чтобы не упасть при повороте? При каком минимальном коэффициенте трения между колесами и дорогой возможен такой поворот?
1.044. К потолку трамвайного вагона подвешен на нити шар. Вагон идет со скоростью v = 18 км/ч по закруглению радиусом R = 50 м. На какой угол а от вертикали отклонится при этом нить с шаром?
1.045. Горизонтальный диск вращается вокруг вертикальной оси с частотой п = 30 об/мин. На расстоянии r= 20 см от оси вращения на диске лежит тело. Каким должен быть коэффициент трения между телом и диском, чтобы тело не соскользнуло с диска?


 1.046.
На невесомом стержне длиной l
= 40см
1.046.
На невесомом стержне длиной l
= 40см
закреплены два
точечных тела массами m1
=100г
О
 и
т2
= 200 г, как
показано на рисунке. Стержень
■
■
и
т2
= 200 г, как
показано на рисунке. Стержень
■
■
 вращается.
в
горизонтальной плоскости
с угловой
m1
m2
вращается.
в
горизонтальной плоскости
с угловой
m1
m2
скоростью = 5 рад/с вокруг оси ОО, проходящей О
через один из концов стержня Рис. к задаче 1.046
Определить силу натяжения стержня между телами и между осью и первым телом.
1.047. Камень, привязанный к веревке длиной l = 50 см, равномерно вращается в вертикальной плоскости. При какой частоте вращений п веревка разорвется, если известно, что она разрывается при силе натяжения, равной десятикратной силе тяжести, действующей на камень?
1.048.Камень,
привязанный к веревке, равномерно
вращается в
вертикальной плоскости.
Найти массу т
камня, если
известно, что
разность между
максимальной и минимальной силами
натяжения веревки
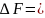 10Н.
10Н.
1.049. Гирька, привязанная к нити длиной l = 29,4 см, описывает в горизонтальной плоскости окружность радиусом R = 14,7 см. С какой частотой п вращается гирька?
1.050. Камень массой т = 0,5 кг, привязанный к веревке длиной l =50 см, равномерно вращается в вертикальной плоскости. Сила натяжения веревки в нижней точке окружности Т = 44 Н. На какую высоту h поднимется камень, если веревка обрывается в тот момент, когда скорость направлена вертикально вверх? Сопротивлением воздуха пренебречь.
1.051.Невесомый стержень длиной l=10 см горизонтально висит на двух невесомых параллельных пружинах, прикрепленных к концам стержня. Жесткости пружин k1 = 2 Н/м и k2 = 3 Н/м. На каком расстоянии от первой пружины надо подвесить груз, чтобы стержень оставался горизонтальным?
1.052.Человек массой m1 = 60 кг, бегущий со скоростью v1 = 8 км/ч, догоняет тележку массой т2 = 80 кг, движущуюся со скоростью v2 = 2,9 км/ч, и вскакивает на нее. С какой скоростью и будет двигаться тележка? С какой скоростью U и в каком направлении будет двигаться тележка, если человек бежал ей навстречу?
1.053. С тележки, свободно движущейся по горизонтальному пути со скоростью v1 = 3 м/с, в сторону, противоположную движению тележки, прыгает человек. Скорость тележки после прыжка стала равной v2 =4 м/с. Какова горизонтальная составляющая скорости V2x человека при прыжке относительно тележки, если масса тележки m1 = 210кг, масса человека т2 = 70 кг.
1.054.Снаряд массой m1 =100 кг, летящий горизонтально вдоль железнодорожного пути со скоростью v1 = 500 м/с, попадает в вагон с песком общей массой т2 =10 ти застревает в нем. Какую скорость v приобрел вагон, если он: а) стоял неподвижно; б) двигался со скоростью v2 =36 км/ч в том же направлении, что и снаряд; в) двигался со скоростью v2=36 км/ч навстречу снаряду?
1.055. Тело массой m1 =2 кг, движущееся горизонтально со скоростью v1 = 1 м/с, неупруго соударяется с телом массой т2 = 0,5 кг. Какую скорость получат тела в результате удара, если второе тело: а) было неподвижно;
б) двигалось со скоростью v2 = 2 м/с в том же направлении, что и первое тело; в) двигалось со скоростью v2 = 2 м/с навстречу первому телу?
1.056. Граната, летящая со скоростью v= 10 м/с, разорвалась на два осколка. Больший осколок, масса которого составляла 0,6 массы всей гранаты, продолжал двигаться в прежнем направлении, но с увеличенной скоростью v1 =25м/с. Найти величину и направление скорости v2 меньшего осколка.
1.057. При горизонтальном полете со скоростью v = 250 м/с снаряд массой т=8 кг разорвался на две части. Большая часть массой m1 = 6 кг получила скорость v1 = 400 м/с в направлении полета снаряда. Определить модуль и направление скорости v2 меньшей части снаряда.
1.058. Снаряд, летевший со скоростью v= 300 м/с, разорвался на два осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростью v1 = 150 м/с. Определить скорость v2 большего осколка.
1.059.На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса его m1 = 60 кг, масса доски т2 = 20 кг. С какой скоростью u (относительно пола) будет двигаться тележка, если человек пойдет вдоль нее со скоростью v=1 м/с (относительно доски)? Трения нет.
1.060. На стальную плиту с высоты h1 = 2 м вертикально вниз падает шарик массой т = 200 г и подпрыгивает на высоту h2 = 0,5 м. Определить импульс р, полученный плитой при ударе. Начальная скорость шарика равна нулю, сопротивлением воздуха пренебречь.
1.061.Определить импульс р, полученный стенкой при ударе о нее шарика массой т= 300 г, если шарик двигался со скоростью v= 8 м/с под углом = 60° к плоскости стенки. Удар о стенку считать упругим.
1.062. Конькобежец
массой М =70
кг, стоя на коньках на льду, бросает в
горизонтальном направлении камень
массой т =
2 кг со скоростью v
= 4 м/с. На
какое расстояние
s
откатится при этом конькобежец,
если коэффициент трения коньков о лед
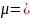 0,01?
0,01?
1.063.Тело массой m1= 5 кг движется навстречу второму телу массой m2= l,5 кг и неупруго соударяется с ним. Скорости тел непосредственно перед ударом были v1 = 2 м/с и v2 = 4 м/с. Какое время t будут двигаться эти тела после удара, если коэффициент трения = 0,05 ?
1.064. На рельсах стоит платформа массой m1 = 10 т. На платформе закреплено орудие массой т2 = 5 т, из которого производится выстрел вдоль рельсов. Масса снаряда т3 = 100 кг, его начальная скорость v0 =500 м/с. На какое расстояние s откатится платформа после выстрела? Коэффициент трения платформы о рельсы = 0,008.
1.065. Два тела движутся навстречу друг другу и соударяются неупруго. Скорости тел до удара v1 = 2 м/с и v2 = 4 м/с. Общая скорость тел после удара равна u = 1 м/с и совпадает с направлением скорости первого тела. Во сколько раз кинетическая энергия Wk1 первого тела была больше кинетической энергии Wk2 второго тела?
1.066. Шар массой m1 = 3 кг движется со скоростью v1 = 2 м/с и сталкивается с покоящимся шаром массой т2 = 5 кг. Какая работа совершается при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.
1.067. Шар массой m1 = 1 кг движется со скоростью v1 = 4 м/с и сталкивается с шаром массой т2= 3 кг, движущимся навстречу ему со скоростью v2 = 4 м/с. Каковы скорости u1 и u2 шаров после удара? Удар считать абсолютно упругим, прямым, центральным.
1.068. Шар массой т1 = 4 кг, движущийся со скоростью v1=5 м/с, сталкивается с шаром массой т2 = 6 кг, который движется в ту же сторону со скоростью v2 = 2 м/с. Определить скорости u1 и u2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
1.069. Шар массой m1 = 5 кг движется со скоростью v1 = 1 м/с и сталкивается с покоящимся шаром массой т2 = 3 кг. Определить скорости u1 и u2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
1.070. Два шарика массами т1 = 20 г и т2 = 10 г подвешены на нитях одинаковой длины, закрепленных в одной точке. Нить с первым шариком отклонили так, что шарик поднялся на высоту h0 = 4,5 см и отпустили. На какую высоту поднимутся шарики после неупругого удара?
1.071. Пуля, летящая горизонтально, попадает в центр шара, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от центра шара до точки подвеса стержня l = 1м. Найти скорость v пули, если известно, что стержень с шаром отклонился от удара пули на угол а = 10° от вертикали.
1.072. Пуля, летящая горизонтально, попадает в центр шара, подвешенного на невесомой нити, и застревает в шаре. Масса пули т1 = 6 г, масса шара т2 = 0,5 кг. Скорость пули v1 = 500 м/с. При каком предельном расстоянии l от центра шара до точки подвеса нити шар после попадания пули поднимется на максимальную высоту?
1.073. В подвешенный на нити длиной l = 1,8 м деревянный шар массой m1 = 8 кг попадает горизонтально летящая пуля массой т2 = 4 г. С какой скоростью летела пуля, если нить с шаром отклонилась от вертикали на угол = 3°? Размером шара пренебречь. Удар пули считать прямым, центральным.
1.074. Стальной шарик
массой т =
20 г, упав вертикально вниз с высоты h1
= 1 м на
горизонтальную стальную плиту,
отскакивает от нее на высоту h2
= 81 см. Найти
импульс силы F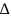 t,
полученный
плитой за время удара, и количество
теплоты Q,
выделившейся
при ударе.
t,
полученный
плитой за время удара, и количество
теплоты Q,
выделившейся
при ударе.
1.075. Нить с подвешенным на ней грузом массой т — 1 кг отклоняют на угол = 30° и отпускают. Найти силу натяжения нити Т в момент прохождения грузом положения равновесия. Трения нет.
1.076. Невесомый стержень с подвешенным на нем грузом массой т=3 кг отклоняют на угол = 90° и отпускают. Найти силу натяжения Т стержня в момент прохождения грузом положения равновесия. Трения нет.
1.077. Груз массой m = 150 кг подвешен на стальной проволоке, выдерживающей силу натяжения Т = 3 кН. На какой наибольший угол можно отклонить проволоку с грузом, чтобы она не разорвалась при прохождении грузом положения равновесия? Трения нет.
1.078. Определить работу, совершенную внешней силой при растяжении двух соединенных последовательно пружин жесткостями k1 =400 Н/м и k2 = 250 Н/м, если первая пружина растянулась на 1= 2 см.
1.079. Две пружины жесткостью k1 = 0,5 кН/м и k2 = 1 кН/м скреплены параллельно. Определить потенциальную энергию П данной системы при абсолютной деформации 1= 4 см.
1.080. Мальчик, стреляя из рогатки, натянул резиновый шнур так, что его длина увеличилась на 10 см. С какой скоростью полетел камень массой m= 20 г? Жесткость шнура k = 1 кH/м.
1.081. С какой скоростью v двигался вагон массой m=20 т, если при ударе об упор каждый буфер сжался на 1= 10 см? Жесткость пружины каждого буфера k = 1 МН/м.
1.082. Вагон массой m = 35 т движется на упор со скоростью v = 0,2 м/с. При полном торможении вагона буферные пружины сжимаются на 1= 12см. Определить максимальную силу Fmax сжатия буферных пружин и продолжительность t торможения.
1,083. При торможении вагона массой т = 16 т, двигавшегося со скоростью v =; 0,6 м/с, пружины буфера сжались на 1= 8 см. Какова общая жесткость k пружин буфера?
1.084. Если на верхний конец вертикально расположенной пружины положить груз, то пружина сожмется на 1= 3 мм. На сколько сожмет пружину тот же груз, упавший на конец пружины с высоты h = 8 см?
1.085. Груз массой т =1 кг падает на чашу весов с высоты Н= 10 см. Каково максимальное показание весов после удара, если после успокоения колебаний чаша весов опустилась на h = 0,5 см? Массой чаши пренебречь.
1.086 - 1.101. Используя теорему Штейнера, рассчитать момент инерции системы тел относительно оси ОО, считая массы шаров, дисков и стержней равными 1кг, длины стержней равными 40 см. Стороны квадратов, а также радиусы дисков, шаров и обручей равны 10 см
86
|
ДИСК |
ШАР |
ДИСК |
90 О
O |
О ДИСК |
92
О
ШАР |
О
ДИСК |
94
ОБРУЧ со спицами |
О О
ДИСК |
96
О О
ШАР |
|
98
ОБРУЧ со спицами
|
99 О
ДИСК с вырезом в центре
|
О ДИСК с
в центре
|
101 О
ОБРУЧ
|
 1.102.
Тонкостенный цилиндр, масса которого
т = 12
кг, а диаметр
основания D
= 30 см,
вращается относительно оси, совпадающей
с осью
симметрии цилиндра, согласно
уравнению
1.102.
Тонкостенный цилиндр, масса которого
т = 12
кг, а диаметр
основания D
= 30 см,
вращается относительно оси, совпадающей
с осью
симметрии цилиндра, согласно
уравнению
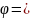 А + Bt
+ Сt3,
где С = 0,2
рад/с3.
Определить действующий на цилиндр
момент сил М в момент
времени t
= 5 с.
А + Bt
+ Сt3,
где С = 0,2
рад/с3.
Определить действующий на цилиндр
момент сил М в момент
времени t
= 5 с.

 1.103.
На шкив маховика намотан шнур, к концу
которого
привязан груз массой т
= 2 кг (рис.
). Определить
момент
1.103.
На шкив маховика намотан шнур, к концу
которого
привязан груз массой т
= 2 кг (рис.
). Определить
момент
инерции I маховика, если он, вращаясь равноускорено Рис. к задаче 1.103
под действием груза, за время t =3 с приобрел угловую скорость = 9 рад/с. Радиус шкива 8 см.
1.104.Через
блок диаметром D
=
20 см перекинута нить с привязанными
к се концам грузами массой mt
= 1,0 кг и т2
= 0,8 кг.
Определить момент инерции I
блока, если под действием грузов он
вращается с угловым ускорением
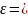 2
рад/с2.
2
рад/с2.
1.105. Стержень массой 2 кг и длиной 60 см вращается вокруг оси, проходящей через его середину, согласно уравнению At + Bi3, где А=2 рад/с; В= 0,2 рад/с . Определить вращающий момент М, действующий на стержень через t =5 с после начала вращения.
1,106, Определить момент силы М, который необходимо приложить к колесу, вращающемуся с частотой п = 4 с-1, чтобы оно остановилось в течение времени t = 10 с. Диаметр колеса D = 50 см. Массу колеса т = 6 кг считать равномерно распределенной по ободу.
1.107. Через блок, имеющий форму диска массой т = 1,2 кг, переброшена нить, к концам которой подвешены грузы массами m1 = 0,3 кг и т2 = 0,7 кг. Определить силы натяжения нити T1 и Т2 по обе стороны блока.
1.108. Барабан в виде однородного цилиндра массой т0 = 9 кг может вращаться без трения около оси, совпадающей с осью симметрии цилиндра. На барабан намотан шнур, к концу которого привязан груз массой т = 2 кг. Найти ускорение а груза.
1.109. На барабан радиусом R = 0,25 м намотан шнур, к концу которого привязан груз массой т = 1 кг. Найти момент инерции I барабана, если известно, что груз опускается с ускорением а = 2 м/с2. Трением пренебречь.
1.110. По ободу шкива, насаженного на общую ось с маховым колесом, намотана нить, к концу которой подвешен груз массой т = 1 кг. На какое расстояние h должен опуститься груз, чтобы колесо со шкивом приобрело частоту вращения n = 60 об/мин? Момент инерции колеса со шкивом I = 0,42 кг.м2, радиус шкива R = 10 см.
1.111. Диск массой т = 2 кг катится без скольжения по горизонтальной плоскости со скоростью v = 1 м/с. Найти кинетическую энергию Wk диска.
1.112. Шар диаметром D = 6 см и массой т = 0,25 кг катится без скольжения по горизонтальной плоскости, делая за одну секунду четыре оборота. Найти кинетическую энергию Wk шара.
1.113. Обруч и диск одинаковой массы mt = т2 катятся без скольжения с одинаковыми скоростями v. Кинетическая энергия обруча Wk1 = 4 Дж. Найти кинетическую энергию Wk2 диска.
1.114. Шар массой т = 1 кг, катящийся без скольжения, ударяется о стенку и откатывается от нее. Скорость шара до удара о стенку 10 см/с, после удара - 5 см/с. Найти количество теплоты Q, выделившееся при ударе iара о стенку.
1.115. Диск диаметром D = 60 см и массой т = 1 кг вращается с частотой п = 20 об/с вокруг оси, проходящей через центр диска перпендикулярно к его плоскости. Какую работу А надо совершить, чтобы остановить диск?
1.116. Определить скорость поступательного движения сплошного цилиндра, скатившегося с наклонной плоскости высотой h = 30 см.
1.117. Обруч катится по горизонтальной дороге со скоростью v = 7,2 км/ч. На какое максимальное расстояние s может вкатиться обруч на горку с подъемом 10 м на каждые 100 м пути?
1.118. Шар радиусом R = 10см и массой 3кг вращается с частотой п = 2об/с вокруг оси, проходящей через его центр. Какую работу А надо совершить чтобы увеличить угловую скорость вращения шара вдвое?
1.119. Шар скатывается без скольжения по наклонной плоскости с высоты h = 0,5 м без начальной скорости. Какую скорость будет иметь шар у основания наклонной плоскости?
1.120. Полый цилиндр с радиусом основания R = 6 см и массой т = 0,5 кг скатывается без проскальзывания по наклонной плоскости с высоты h =0,9 м из состояния покоя. За какое время t скатится цилиндр? Угол наклона плоскости к горизонту = 30°.
1.121. Колесо, вращаясь равно замедлено, уменьшило за время t =1 мин частоту вращения от п1 = 300 об/мин до п2 -= 180 об/мин. Момент инерции колеса I = 1,5 кг.м2. Найти момент сил торможения М и работу сил торможения А, совершенную за одну минуту.
1.122. Маховик вращается с частотой п = 10 об/с. Его кинетическая энергия Wk =7,85 кДж. За какое время t угловая скорость маховика увеличится вдвое под действием момента сил, равного М = 50 H-м?
1.123.К ободу диска массой т= 5 кг приложена касательная сила F=19,6 Н. Какую кинетическую энергию Wk будет иметь диск через время t = 5с после начала действия силы?
1.124. Однородный стержень длиной l = 1 м подвешен на горизонтальной оси, проходящей через верхний конец стержня. На какой угол надо отклонить стержень, чтобы нижний конец стержня при прохождении положения равновесия имел скорость v = 5 м/с? Трения нет.
1.125. Однородный стержень длиной l = 85 см подвешен на горизонтальной оси, проходящей через верхний конец стержня. Какую скорость v надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси? Трения нет.
1.126. Платформа в виде горизонтально расположенного диска вращается по инерции с частотой п1 = 8 об/мин вокруг вертикальной оси, проходящей через центр диска. На краю платформы стоит человек массой т = 70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой п2 = 10 об/мин. Определить массу т1 платформы. Момент инерции человека рассчитывать как для материальной точки. Трения нет.
1.127. На краю неподвижной скамьи Жуковского диаметром D = 0,8 м и массой т1 = 6 кг стоит человек массой т2 = 60 кг. С какой угловой скоростью начнет вращаться скамья, если человек поймает летящий на него мяч массой т3 = 0,5 кг? Траектория мяча горизонтальна и проходит на расстоянии r = 0,4 м от оси скамьи. Скорость мяча v = 5 м/с. Момент инерции человека рассчитывать как для материальной точки. Трения нет.
1.128. В центре скамьи Жуковского стоит человек и держит в руках стержень вертикально по оси вращения скамьи. Скамья с человеком вращается с угловой скоростью = 4 рад/с. С какой угловой скоростью будет вращаться скамья, если человек повернет стержень так, чтобы он занял горизонтальное положение? Суммарный момент инерции человека и скамьи 1=5 кг.м2. Длина стержня / = 1,8 м, масса т =6 кг. Считать, что центр масс стержня с человеком находится на оси платформы. Трения нет.
1.129. Платформа в виде диска диаметром D =3 м и массой m1 = 180 кг может вращаться без трения вокруг вертикальной оси, проходящей через центр диска. С какой угловой скоростью будет вращаться платформа, если по ее краю пойдет человек массой т2 = 70 кг со скоростью v =1,8 м/с относительно платформы? Момент инерции человека рассчитывать как для материальной точки.
1.130. Платформа, имеющая форму диска, может вращаться без трения около вертикальной оси, проходящей через центр диска. На краю платформы стоит человек. На какой угол повернется платформа, если человек пойдет вдоль края платформы и, обойдя ее, вернется в исходную (на платформе) точку? Масса платформы m1 = 280 кг, масса человека m2 = 80 кг. Момент инерции человека рассчитывать как для материальной точки.
1.131. Горизонтальная платформа в виде диска массой т = 100 кг вращается с частотой nt = 10 об/мин вокруг вертикальной оси, проходящей через центр платформы. Человек массой т0 = 60 кг стоит при этом на краю платформы. С какой частотой п2 , начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Момент инерции человека рассчитывать как для материальной точки. Трения нет.
1.132. По условию задачи 1.131 определить работу А, совершенную человеком при переходе от края платформы к ее центру. Радиус платформы R= 1,5 м.
1.133. Горизонтальная платформа в виде диска массой т = 100 кг и радиусом R = I м вращается с частотой nt = 20 об/мин около вертикальной оси, проходящей через центр диска. В центре платформы стоит человек и держит в вытянутых в стороны руках гири. С какой частотой n2 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I1= 2,94 кг.м2 до I2 = 0,98 кгм2? Трения нет.
1.134. По условию зад. 1.133 определить работу А, совершенную человеком при перемещении гирь вниз.
1.135. Человек массой ти = 60 кг находится на неподвижной платформе в виде диска массой т= 100 кг, который может вращаться без трения около вертикальной оси, проходящей через центр диска. С какой частотой п будет вращаться платформа, если человек пойдет с постоянной скоростью v0 = 4 км/ч относительно платформы по окружности радиусом r = 1,5 м вокруг оси вращения? Радиус платформы R = 2м. Момент инерции человека рассчитывать как для материальной точки.
1.136. Шар массой т= 0,5 кг и радиусом R = 0,1 м вращается вокруг оси, проходящей через его центр, согласно закону 2 + 2t - t2. Определить изменение момента импульса шара в интервале времени от t1 = 0 до момента времени t2, когда шар остановился. Какую работу совершили за это время силы, действующие на шар?
1.137. В центре вращающегося столика стоит человек, держащий на вытянутых руках две гири на расстоянии l = 1,5 м друг от друга. Столик совершает один оборот в секунду. Определить работу, которую совершит человек при перемещении гирь в центр столика. Масса одной гири т = 4 кг. Момент инерции столика вместе с человеком I = 0,95 кгм2. Трения нет.
1,138,Материальная точка совершает гармонические колебания с амплитудой А = 15 см. Максимальная скорость точки vmах = 30 см/с. Определить максимальное ускорение атах точки.
1.139. Точка совершает гармонические колебания согласно уравнению:
х = Asin t, где А - 5 см, = 2 с-1. Через какое минимальное время t после прохождения точкой положения равновесия на нее действует возвращающая сила величиной F = 5 мН, и потенциальная энергия точки равна П =О,1 мДж?
1,140, Определить период Т гармонических колебаний диска радиусом
R = 40 см около горизонтальной оси, проходящей через образующую диска.
1.141. На невесомом стержне длиной l = 30 см укреплены два грузика: один - в середине стержня, другой - на одном из его концов. Стержень с грузиками колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить приведенную длину L и период Т гармонических колебаний стержня.
1.142. Найти максимальную кинетическую энергию Тпах материальной точки массой m = 2 г, совершающей гармонические колебания с амплитудой А=4 см и частотой v = 5 Гц.
Однородный стержень длиной l = 0,5 м совершает малые колебания в вертикальной плоскости около горизонтальной оси, проходящей через один из концов стержня. Найти период колебаний Т стержня.
Найти период малых колебаний однородного стержня длиной 0,5 м около горизонтальной оси, проходящей через точку, находящуюся на расстоянии 10 см от его верхнего конца.
1.145. На концах невесомого вертикального стержня длиной l укреплены два одинаковых груза. Период малых колебаний стержня с грузами около горизонтальной оси, проходящей через точку на расстоянии 1/4 от одного из грузов, равен Т =2 с. Какова длина стержня?
1.146. Обруч диаметром D = 62,5 см висит на гвозде, вбитом в стену, и совершает малые колебания в плоскости, параллельной стене. Найти период колебаний T обруча.
1.147.
Небольшой груз совершает колебания по
закону: х
= 0,02sin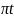 (все
величины даны в единицах СИ). Через
какое минимальное время после прохождения
положения равновесия груз имеет
смещение, равное половине амплитуды
колебаний?
(все
величины даны в единицах СИ). Через
какое минимальное время после прохождения
положения равновесия груз имеет
смещение, равное половине амплитуды
колебаний?
1.148. Материальная точка совершает гармонические колебания с амплитудой A= 0,03 м и периодом T= 0,2 с. Записать уравнение колебаний, определить смещение, скорость и ускорение точки при t = 0,1 с, считая, что в момент времени t0 = 0 точка проходит положение равновесия.
1.149. Тело совершает гармонические колебания по закону: х = 0,1sin (все величины даны в единицах СИ). Определить скорость и ускорение тела в момент времени t = 0,5 с.
1.150. Тело совершает гармонические колебания по закону: х = 0,6sin2nt (все величины даны в единицах СИ). Определить максимальные значения скорости и ускорения тела.
1.151. Тело массой т = 0,5 кг подвешено на пружине, жесткость которой k = 200 Н/м. Определить частоту свободных колебаний этой системы.
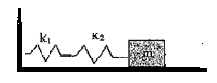
Определить частоту колебаний пружинного маятника, изображенного на рис. Коэффициенты жесткости пружин равны k1= 80 Н/м и k2 =100 Н/м, масса груза т = 0,5 кг.
Определить частоту колебаний пружинного маятника, изображенного на рис. Коэффициенты жесткости пружин равны k1 = 75 Н/м и k2 = 95 Н/м, масса груза т = 0,5 кг.
Определить частоту колебаний пружинного маятника, изображенного на рис. Коэффициенты жесткости пружин равны k1 = 300 Н/м и k2 = 200 Н/м, масса груза т = 0,5 кг.


![]()
Рис. к задаче 1.152 Рис. к задаче 1.153 Рис. к задаче 1.154

 О
О


 l
O
l
O

 87
О
87
О
 88
О
88
О

 89
О
89
О

 l
l
 91
91

 93
93

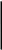
 О
О


 95
95

 97
97

 О
О
 ДИСК
ДИСК О О
О О



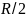

 100
100
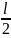
 вырезом
вырезом

