4.2 Примеры решения задач

При решении задач о движении заряженной частицы в электрическом и магнитном полях, напряженность и индукция которых и , рекомендуется придерживаться следующей схемы:

1. сделать рисунок, указать направление векторов и , а также направление скорости частицы, отметить знак ее заряда;

2. если вектор скорости частицы направлен под углом к вектору индукции магнитного поля, то вектор скорости следует разложить на два составляющих вектора - параллельный и перпендикулярный вектору магнитной индукции;

3. расставить все силы, действующие на частицу;

4. спроектировать каждую силу на две оси - параллельную вектору скорости и перпендикулярную ему;

5. записать основное уравнение динамики материальной точки для каждой оси.

При рассмотрении движения проводника (или контура) с током в однородном магнитном поле рекомендуется:

1. нарисовать проводник (или контур) с током, указать направление вектора магнитной индукции;

2. применив правило левой руки, определить направление сил, действующих на проводник (или каждый элемент контура) со стороны магнитного поля; нарисовать векторы этих сил;

3. расставить все остальные силы, если они есть, действующие на проводник (или контур);

4. записать условие равновесия проводника (или контура) с током, если он находится в состоянии равновесия.

Применяя закон электромагнитной индукции, следует:

1. установить причины изменения магнитного потока, связанного с контуром;

2. записать выражение для магнитного потока и найти его изменение Ф за некоторый промежуток времени t;

3. подставить Ф в уравнение для ЭДС индукции и решить это уравнение относительно искомой величины.

Если электрическая цепь содержит помимо обычных источников тока участки, в которых возникает ЭДС индукции, вызванная движением проводника в магнитном поле, то нужно:

1. определить величину и полярность ЭДС;

2. перерисовать схему электрической цепи, заменив участок возникновения ЭДС индукции, источником тока с учетом полярности;

3. провести расчет обычной цепи постоянного тока с несколькими источниками ЭДС.

Пример 1

Электрон, движущийся со скоростью , попадает в однородные электрическое и магнитное поля, напряженность и магнитная индукция

в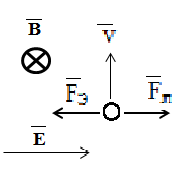 заимно перпендикулярны. Скорость электрона перпендикулярна векторам и .

Как будет двигаться электрон в начальный малый

промежуток времени? При каком условии электрон будет двигаться равномерно и прямолинейно?

Решение

Пусть векторы , и направлены так, как это показано на рис.4.2. Со стороны электрического поля

Рис 4.2 на электрон действует сила

F_э= eE,

а со стороны магнитного поля - сила Лоренца, равная

F_л = evB,

где е - заряд электрона.

Направления сил и , показаны на рис. 2.

Если (например, F_э > F_л;), то равнодействующая этих сил будет направлена перпендикулярно скорости электрона и будет сообщать электрону центростремительное ускорение

Если F_э = Е_л, т.е. Е В, то электрон будет двигаться равномерно и прямолинейно.

Пример 2

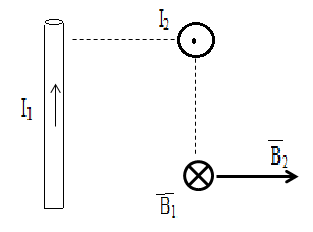О пределить индукцию магнитного поля В, созданного двумя прямыми бесконечно длинными перпендикулярными взаимно

проводниками, расположенными на расстоянии а друг от друга, в точке А, удаленной от

каждого проводника на расстояние а. Силы тока в проводниках одинаковы и равны I.