4. Магнетизм

4.1 Основные понятия и формулы

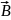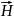1. Связь магнитной индукции с напряженностью магнитного поля

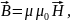
где – магнитная проницаемость среды; в вакууме ;

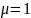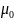= 4π∙10^-7 Гн/м - магнитная постоянная.

2. На частицу зарядом q, движущуюся со скоростью в магнитном поле индукции действует сила Лоренца:

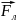=q .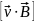

3. Магнитная индукция, создаваемая элементом тока I∙dlв точке пространства, характеризующейся относительно элемента тока радиус – вектором 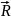равна:

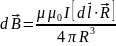
4. Индукция магнитного поля на расстоянии R от бесконечно длинного прямого проводника, по которому течет ток силой I:

.

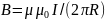5. Индукция магнитного поля в центре кругового витка радиусом, по которому течет ток силой I:

.

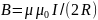6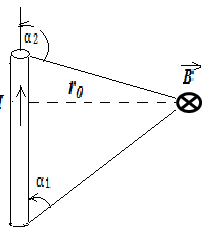 . Индукция магнитного поля на оси кругового витка радиуса R, по которому течет ток силой I, на расстоянии h от центра витка:

.

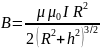7. Индукция магнитного поля, созданного отрезком I

провода с током силой I (рис.4.1)

.

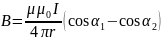8. Индукция магнитного поля бесконечно длинного Рис.4.1

соленоида с током силой I:

.

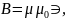где n– количество витков, приходящихся на единицу длины соленоида.

9. На проводник длиной l, по которому течет ток силой I, находящийся в магнитном поле индукции 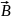, действует сила

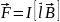
10. Два параллельных провода длиной l каждый с токами I₁ и I₂ взаимодействуют с силой

F =

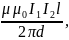
где d– расстояние между проводами.

11. Магнитный момент плоского контура площадью S с током Iравен

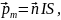
где 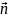– единичный вектор, перпендикулярный к плоскости контура, и направление которого связано с направлением тока в контуре правилом правого винта.

12. Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле

= .

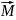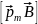13. Потенциальная энергия (обусловленная существованием механического момента) контура с током во внешнем магнитном поле

W_пот = -( _.

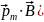14. Магнитный поток

а) в случае однородного магнитного поля и плоской поверхности

Ф = BScosα,

где S– площадь контура,

α- угол между нормалью к плоскости контура и вектором магнитной индукции;

б) в случае неоднородного поля и произвольной поверхности

Ф = .

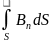15. Потокосцепление (полный поток)

 = N Ф .

Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу витков.

16. Работа, совершаемая магнитным полем по перемещению контура с током I

A = I∆ Ф .

17. При изменении магнитного потока, пронизывающего контур, в контуре возникает ЭДС индукции

Ε = - .

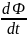18. Разность потенциалов на концах проводника длиной l, движущегося со скоростью v в магнитном поле индукции B

U = Blvsinα

где α – угол между векторами .

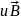19. Заряд, протекающий по замкнутому контуру сопротивлением R при изменении магнитного потока, проникающего этот контур

= . .

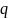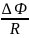20. Индуктивность контура

L =

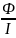
21. ЭДС самоиндукции

ε = -

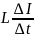
22. Индуктивность соленоида

L = ,

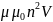где V– объем соленоида,

n - отношение числа витков соленоида к его длине. –

23.Мгновенное значение силы тока в цепи, обладающей сопротивлением и индуктивностью

а)при замыкании цепи на источник тока

i = ,

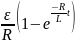где ε – ЭДС источника тока;

t – время, прошедшее после замыкания цепи;

б)при размыкании цепи и источника тока

i =I₀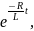

где I_{0 –}сила тока на момент t = 0

24.Энергия магнитного поля контура с током (или соленоида)

W = .

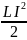25. Объемная плотность энергии магнитного поля

W = = = .

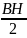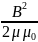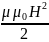26. Период колебаний магнитной стрелки (или контура с током), обладающей магнитным моментом 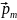и находящийся в магнитном поле индукции :

T = 2π .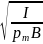

где I – момент инерции стрелки (контура) относительно оси подвеса.