3.4. Задачи для самостоятельного решения

3.001. Два одинаковых маленьких шарика 10 г. каждый подвешены на нитях длиной 120 см в одной точке и несут на себе одинаковые электрические заряды. Расстояние между шариками 5 см. Каковы заряды шариков?

3.002. Три маленьких шарика массой 10 г подвешены на шелковых нитях по 1 м, сходящихся наверху в одном узле (рис. 1).шарики одинаково заряжены и находятся в горизонтальной плоскости, образуя равносторонний треугольник со стороной 0,1 м. Каков заряд каждого шарика?

3.003. В каждом из двух других противоположных углах того же квадрата помещено по заряду Q. В двух других противоположных углах того же квадрата помещено по заряду q. Если результирующая сила, действующая на заряд Q, равна нулю, чему равен заряд Q, выраженный через заряд q?

3.004. Как далеко друг от друга должны быть расположены два протона, если отталкивающая кулоновская сила, действующая на один из них, равна силе гравитационного притяжения, действующей на протон со стороны Земли?

3.005. Некоторый заряд требуется поделить на части (Q-q) и q . Каково будет отношение между Q и, q, если эти заряды, расположенные на заданном расстоянии друг от друга, должны испытывать максимальное кулоновское отталкивание?

3.006. Каждый из двух маленьких шариков максимально заряжен так, что их общий заряд равен 5∙10^-5 Кл. Как распределен этот заряд между ними, если, находясь на расстоянии 2 м друг от друга, они отталкиваются с силой 1Н?

3.007. Три одинаковых точечных заряда по 2 нКл каждый находится в вершинах равностороннего треугольника со стороной 10 см. Определить модуль и направление силы, действующей на один из зарядов со стороны других?

3.008. Два положительных точечных заряда закреплены на расстоянии 100 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд, чтобы он находился в равновесии?

3.009. Четыре одинаковых точечных заряда по 40 нКл каждый закреплены в вершинах квадрата со стороной 10 см. Найти силу, действующую на один из этих зарядов со стороны трех остальных?

3.010. На расстоянии 20 см находятся два точечных заряда – 50 нКл и 100 нКл. Определить силу, действующую на заряд – 10 нКл, удаленный от обоих зарядов на расстояние 20 см?

3.011. Расстояние между двумя точечными зарядами 2 нКл и 4 нКл равно 60 см. Определить положение точки, в которой нужно поместить третий заряд так, чтобы система находилась в равновесии. Определить величину и знак этого заряда.

3.012. На тонком кольце равномерно распределен заряд с линейной плотностью заряда 0,2 нКл/см. Радиус кольца 15 см. На серединном перпендикуляре к плоскости кольца находится заряд 10 нКл. Определить силу, действующую на заряд со стороны кольца, если он удален от его центра на 20 см?

3.013. Два шарика, имеющих одинаковые массы и радиусы, подвешены на нитях одинаковой длины так, что их поверхности соприкасаются. После сообщения шарикам заряда 0,4 мкКл, они оттолкнулись друг от друга и разошлись на угол 60⁰. Найти массу каждого шарика, если расстояние от центра шарика до точки подвеса 20 см?

3.014. В вершинах правильного шестиугольника расположены три положительных и три отрицательных заряда. Найти напряженность электрического поля в центре шестиугольника при различных комбинациях в расположении зарядов.

3.015.Два точечных заряда 7,5 нКл и -14,7 нКл расположен

на расстоянии 5 см друг от друга. Найти напряженность электри

ческого поля в точке, находящейся на расстоянии 3 см от положи

тельного заряда и 4 см от отрицательного?

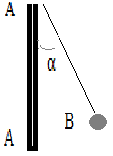
3.016. На рис.3.5 АА – заряженная бесконечная плоскость

с поверхностной плотностью заряда 40 мкКл/м² и В – пробный Рис.3.5

заряд величиной 1 нКл, находящийся на шарике массой 1 г. Какой угол α с плоскостью АА образует нить, на которой висит шарик?

3.017. Точечный заряд q = 0,1 мкКл находится в центре незаряженной тонкой металлической сферы радиуса R = 15 см. Воспользовавшись теоремой Остроградского – Гаусса, найдите зависимость напряженности электрического поля Е от расстоянии до заряда для точек внутри сферы и вне ее. Вычислить напряженность электрического поля на расстоянии r = 20 см от заряда.

3.018. Точечный заряд 0,1 мкКл помещен в центре куба с ребром 0,5 м. Вычислить поток напряженности электрического поля через поверхность куба.

3.019.¹ * Бесконечно длинный тонкий стержень равномерно заряжен с линейной плотностью заряда q = 20 мкКл/м. Пользуясь теоремой Остроградского – Гаусса, получите вид зависимости напряженности электрического поля от расстояния до стержня. Определите величину напряженности поля в точке, находящейся на расстоянии 2 см от стержня.

3.020.* Бесконечная плоскость заряжена с поверхностной плотностью заряда σ = 4 мкКл/м². Пользуясь теоремой Остроградского – Гаусса, получить выражение для напряженности электрического поля, создаваемого этой плоскостью. Определить силу F, действующую со стороны плоскости на заряд q = 100 нКл, находящийся над плоскостью.

3.021.* Заряд равномерно распределен по всему объему бесконечно длинного цилиндра радиуса R.

а ) Показать, что напряженность электрического поля на расстоянии r < R от оси цилиндра определяется выражением: E =

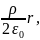
где ρ – объемная плотность заряда цилиндра.

б) Какова напряженность Е при расстоянии r> R?

3.022. На рис. 3.6 изображена непроводящая оболочка Рис.3.6.

сферической формы с объемной плотностью заряда ρ. Изобразить на графике зависимость E = f(r), где 0≤ r≤ 30 см, если ρ = 10^-6Кл/м³ а =10 см, b = 20 см.

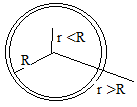
3.023. На рис. 3.7 изображено поперечное сечение длинной тонкостенной металлической трубы радиусом R, несущей на себе заряд с линейной плотностью τ. Получить зависимость E = f(r) , где r– переменное расстояние от оси трубы, причем r ≤ R и. r> R. Изобразить график зависимости

Рис..3.7 E =.f(r) в пределах 0 ≤ r ≤ 5см при τ =2∙10^-8Кл/м и R = 3см.

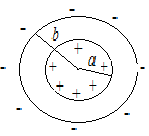3.024.На рис.3.8 изображены сечения двух концентрических цилиндров с радиусами а и b. Цилиндры несут на себе равные по величине и противоположные по знаку заряды с линейной плотностью τ. Доказать, что при r > b и r < а напряженность Е = 0, а между цилиндрами она определяется выражением

Е = 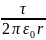, Рис.3.8

3.025. К бесконечной равномерно заряженной вертикальной плоскости подвешен на нити одноименно заряженный шарик массой m = 50 мг и зарядом. q =0,6 нКл. Натяжение нити, на которой висит шарик, Т = 0,7 мН. Найти поверхностную плотность заряда σ плоскости, считая ее заряженной равномерно.

3.026. С какой силой (на единицу длины) взаимодействуют две заряженные бесконечно длинные параллельные нити с одинаковой линейной плотностью заряда τ =20 мкКл/м, находящиеся на расстоянии r = 10 см друг от друга?

3.027. Поверхностная плотность заряда σ бесконечно протяженной вертикальной плоскости равна 400 мКл/м². К плоскости на нити подвешен заряженный шарик массой m = 10г. Определить заряд q шарика, если нить образует с плоскостью угол α = 30°.Плоскость считать заряженной равномерно.

3.028. Поле создано бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда σ = 40 нКл/м². Определить разность потенциалов ∆φ двух точек, отстоящих от плоскости на расстоянии r₁=15см и r₂ =20см.

3.029. Четыре одинаковых капли ртути, заряженные до потенциала φ=10В, сливаются в одну каплю. Каков потенциал образовавшейся капли?

3.030. Тонкий стержень согнут в кольцо радиусом R =10 см. Он равномерно заряжен линейной плотностью заряда τ = 800 нКл/м. Определить потенциал в точке, расположенный на оси кольца на расстоянии r =10 см от его центра.

3.031.Электрическое поле создано бесконечно длинной заряженной нитью, линейная плотность заряда которой τ = 20 нКл/м. Определить разность потенциалов ∆φ двух точек, отстоящих от нити на расстоянии r₁=8 см и r₂ =12 см.

3.032. Поверхностная плотность заряда пластины бесконечно больших размеров равна σ = 10^-7Кл/м². На каком расстоянии друг от друга находятся эквипотенциальные поверхности, если их потенциалы отличаются на 5В?

3.033. Два проводящих шара, радиусы которых равны 10 см и 5 см, заряженные до потенциалов 20 В и 10 В, соединяются тонким проводником. Найти поверхностные плотности зарядов шаров после их соединения. Расстояние между шарами велико по сравнению с их радиусами.

3.034. На прямой, соединяющей два точечных заряда +q и -3q, находящихся на расстоянии 1 м друг от друга. Найти точки, в которых напряженность и потенциал поля равны нулю.

3.035. Точечный заряд q = 10^-6 нКл создает электрическое поле. Точка А находится на расстоянии 2 м, а точка В на расстоянии 1 м от заряда. Чему равна разность потенциалов двух точек А и В, если они расположены в диаметрально противоположных направлениях? Чему равна эта разность, если отрезки qА и qВ взаимно перпендикулярны?

3.036. Ион атома лития Li⁺ прошел разность потенциалов 400 В, ион атома натрия Na⁺ – разность потенциалов 300 В. Найти отношение скоростей этих ионов.

3.037. Шарик массой 1 г и зарядом q=10 нКл перемещается из точки 1, потенциал которой 600 В, в точку 2, потенциал которой равен нулю. Найти его скорость в точке 1, если в точке 2 она стала равной 20 см/с.

3.038. Электрическое поле создано положительно заряженной бесконечно длинной нитью. Двигаясь под действием этого поля от точки, находящейся на расстоянии 1 см от нити, до точки, находящейся на расстоянии 4 см, частица изменила свою скорость от 2∙10⁵ м/с до 3∙10⁵ м/с. Найти линейную плотность заряда нити.

3.039. Около заряженной бесконечно протяженной плоскости находится пробный заряд 0,66 нКл. Заряд перемещается по линии напряженности поля на расстояние 2 см, при этом совершается работа 0,5 Дж. Найти поверхностную плотность заряда плоскости.

3.040. Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобретает скорость ∙10⁶ м/с. Расстояние между пластинами 5,3 мм. Найти разность потенциалов между пластинами, напряженность поля внутри конденсатора и поверхностную плотность заряда на пластинах.

3.041. Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобретает скорость 2∙10⁶ м/с. Расстояние между пластинами 6 мм. Найти разность потенциалов между пластинами и поверхностную плотность заряда на пластинах.

3.042. Электрон в однородном электрическом поле получает ускорение. 10¹² м/с². Найти напряженность электрического поля, скорость, которую получает электрон за 1 мкс своего движения, работу сил электрического поля за это время и разность потенциалов, пройденную при этом электроном. Начальная скорость электрона равна нулю.

3.043. Электрон движется в плоском, горизонтально расположенном конденсаторе параллельно его пластинами со скоростью 3,6∙10⁷ м/с. Напряженность поля внутри конденсатора 3,7 кВ/м, длина пластин конденсатора 20 см. На какое расстояние сместится электрон в вертикальном направлении под действием электрического поля за время его движения в конденсаторе?

3.044. В двух вершинах равностороннего треугольника помещены заряды 20мкКл и -20мкКл. Сторона треугольника равна 5см. Найти потенциал электрического поля в третьей вершине треугольника и вычислить энергию системы зарядов.

3.045. В вершинах квадрата со стороной 5см находятся точечные заряды q, 2q,3q и 4q, расположенные по ходу часовой стрелки. Вычислить энергию системы зарядов, считая q=10мкКл.

3.046. Шарик массой 40 мг, имеющей положительный заряд 1нКл, движется со скоростью 10 м/с. На какое расстояние шарик может приблизиться к другому неподвижному шарику, имеющему положительный заряд 1,33 нКл? Размерами шариков пренебречь.

3.047. До какого расстояния могут сблизиться два электрона, если они движутся навстречу друг другу с относительной скоростью 10⁶м/с?

3.048. Два шарика с зарядами 6,66 нКл и 13,33 нКл находятся на расстоянии 40 см. Какую работу нужно совершить, чтобы сблизить их до расстояния 25см?

3.049. Какая работа совершается при перенесении пробного заряда 20 нКл из бесконечности в точку, находящуюся на расстоянии 1 см от поверхности шара радиусом 1 см с поверхностной плотностью заряда 10 мкКл/м²?

3.050. В вершинах квадрата, сторона которого равна 1 мм, находятся четыре протона. Освободив один из них, дают ему возможность двигаться под действием сил поля оставшихся протонов. Какова скорость протона на бесконечности?

3.051. Три электрона расположены в вершинах равностороннего треугольника, сторона которого равна 1 мкм. Освободив один из них, ему дают возможность свободно перемещаться в поле оставшихся электронов. Определить скорость электрона на бесконечности?

3.052. Два конденсатора с воздушным зазором, емкостью 200 пФ каждый, соединяют последовательно и подключают к источнику с ЭДС 20 В. Как изменятся заряды конденсаторов, если один из них погрузить в жидкий диэлектрик с диэлектрической проницаемостью, равной 4?

3.053. Конденсатор емкостью 100 пФ, имеющей заряд 2 нКл, соединяют через резистор с конденсатором, заряд и емкость которого соответственно равны 4 нКл и 200 пФ?

3.054. Заряды обкладок двух конденсаторов емкостью 100 пФ и 300 пФ одинаковы и равны 10 нКл. Какой заряд пройдет по проводам, если соединить одноименно заряженные обкладки?

3.055. Два конденсатора емкостью 5 мкФ и 8 мкФ соединены последовательно и присоединены к батарее с ЭДС 80 В. Определить заряды конденсаторов и напряжения на них.

3.056. Два одинаковых плоских воздушных конденсатора емкостью 12мкФ соединены последовательно и подключены к источнику с ЭДС 12 В. Определить, на сколько изменится напряжение на одном из конденсатов, если другой погрузить в трансформаторное масло?

3.057. Два металлических шарика радиусами 5 см и10 см имеют заряды 4нКл и -20 нКл, соответственно, и находятся далеко друг от друга. Найти количество теплоты, которое выделится при соединении шариков проводниками. Электроемкостью проводника пренебречь.

3.058 Площадь пластин плоского воздушного конденсатора равна 0,01 м², расстояние между ними 1 мм. К пластинам приложена разность потенциалов 0,1 кВ. Пластины раздвигаются до расстояния 25 мм. Найти энергии конденсатора до и после раздвижения пластин, если источник напряжения перед раздвижением: а) не отключается; б) отключается.

3.059. Плоский конденсатор заполнен диэлектриком и на его пластины подана некоторая разность потенциалов. Его энергия при этом равна 20 мкДж. После того как конденсатор отключили от источника напряжения, диэлектрик вынули из конденсатора. Работа, совершенная при вынимании диэлектрика, равна 70 мкДж. Найти диэлектрическую проницаемость диэлектрика.

3.060. Конденсатор емкостью 100 пФ заряжается до разности потенциалов 50 В. После этого зарядная батарея отключается, а заряженный конденсатор присоединяется параллельно к другому конденсатору. Если измеренная ранее разность потенциалов падает после присоединения до 25 В, то какова емкость второго конденсатора?

3.061. Плоский конденсатор с площадью пластин S =0.01 м² каждая заряжен до разности потенциалов 2кВ. Расстояние между пластинами 2 см. Диэлектрик – стекло. определите энергию поля конденсатора и плотность энергии поля.

3.062. Пластина из диэлектрика толщиной b находится между обкладками плоского конденсатора. Расстояние между обкладками равно d площадь обкладок S, проницаемость диэлектрика ε. Показать, что емкость такого конденсатора равна С = .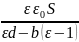

3.063. К батарее с ЭДС ε = 300 В подключены два конденсатора емкостью C₁ =2 пФ и C₂ =3 пФ. Определить заряды и напряжение на конденсаторах при их последовательном соединении.

3.064. К батарее с ЭДС ε = 300 В подключены два конденсатора емкостью . C₁ =2 пФ и C₂ =3 пФ определите заряды и напряжение на конденсаторах при их параллельном соединении.

3.065. Конденсатор емкостью C₁ =600 мкФ зарядили до разности потенциалов 1,5 кВ и отключили от источника напряжения. Затем к конденсатору присоединили параллельно второй, незаряженный конденсатор С₂ емкостью 400 мкФ. Сколько энергии, запасенной в первом конденсаторе, было израсходовано на образование искры, проскочившей при соединении конденсаторов?

3.066. Малый, но все же измеримый ток силой 10^-10А, протекает по медной проволоке диаметром 2,5 мм. Вычислить скорость поступательного движения электронов в проводнике. Число свободных электронов в 1 см³ проводника принять равным 10²³.

3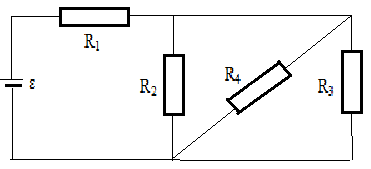 .067. Определить число электронов, проходящих в секунду через площади поперечного сечения железной проволоки длиной 20 м при напряжении на ее концах 16 В.

3.068. Каково эквивалентное сопротивление

сложной цепи, изображенной на рис.3.9? Какие

токи текут по каждому сопротивлению? Принять

R₁ = 100 Ом, R₂ = R₃ = 50 Ом, R₄ = 75 Ом и ε = 6В.

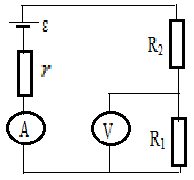Рис.3.9

3.069. В схеме на рис.3.10 ε = 6В, r =2 Ом, R₁ = 5 Ом, R₂ = 4 Ом. Если сопротивление амперметра R_А = 0,1 Ом, то какая ошибка (в процентах) получится при измерении тока, считая сопротивление вольтметра очень большим?

3.070.Ток в проводнике меняется со временем по закону I = 4+2t, где I–сила тока в амперах и t –время в секундах.

Рис.3.10 Какой заряд пройдет через поперечное сечение проводника за

время от t₁ =2c до t₂ =5c . При каком постоянном токе через поперечное сечение проводника за то же время проходит такой же заряд?

3.071. Имеется предназначенный для измерения токов до 15 мА амперметр с сопротивлением 5 Ом. Какое сопротивление нужно взять и как его включить, чтобы этим прибором можно было измерять: а) ток до 150 мА; б) разность потенциалов до 150 В?

3.072. В сеть с напряжением 100 В подключили катушку с сопротивлением 2 кОм и вольтметр, соединенные последовательно. Показание вольтметра 80 В. Когда катушку заменили другой, вольтметр показал 60 В. Определить сопротивление второй катушки.

3.073.Сила тока в проводнике изменяется со временем по закону i =I₀sinωt. Найти заряд, протекающий через поперечное сечение проводника за время, равное половине периода, если сила тока I₀ =10A, циклическая частота ω =50π c^-1.

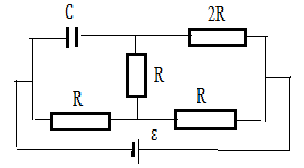
3.074. Определить заряд на конденсаторе (рис.3.11), если его емкость равна 20 мкФ , а ЭДС источника - 50 В.

R 2R А 2С B 3C r 3R V

Риc.3.11 Рис.3.12 Рис.3.13

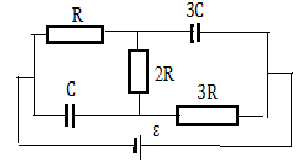
3.075. Определить заряды на обкладках обоих конденсаторов в схеме на рис. 3.12, если ЭДС источника ε =40 В, а С = 100 пФ.

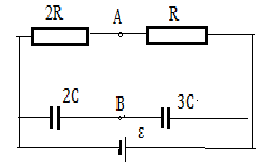
3.076. Определите разность потенциалов между точками А и В в схеме на рис.3.13, учитывая, что ЭДС источника ε =48 В.

3.077. При внешнем сопротивлении R₁ = 8 Ом сила тока в цепи I₁ =0,8A, при сопротивлении R₂ = 15 Ом сила тока I₂ =0,8A. Определить силу тока короткого замыкания I_кэ источника ЭДС

3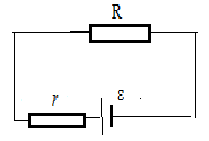 .078.Определить заряд, прошедший по проводнику сопротивлением 3 Ом при равномерном нарастании напряжения на концах провода от U₁=2В до U₂=4В в течение 20 с.

3. 079. Пользуясь рисунком 3.14, показать, что мощность

Р, выделяемая на сопротивлении R в форме джоулева тепла,

максимальна при R = r Показать, что Р_мах = 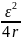, Рис.3.14.

где ε- ЭДС источника,

r- его внутреннее сопротивление.

3.080. Имеется 120 – вольтовая электрическая лампочка мощностью 40 Вт. Какое добавочное сопротивление надо включить последовательно с лампочкой, чтобы она давала нормальный накал при напряжении 220 В?

3.081. Найти внутреннее сопротивление генератора, если известно, что мощность, выделяющаяся во внешней цепи, одинакова при внешних сопротивлениях R₁ =5 Ом, R₂ = 0,2 Ом.

3.082. Элемент замыкают сначала на внешнее сопротивление 2 Ом, затем на внешнее сопротивление 0,5 Ом. Найти ЭДС элемента и его внутреннее сопротивление, если известно, что в каждом из этих случаев мощность, выделяющаяся во внешней цепи, одинакова и равна 2,54 Вт

.

3.083. Разность потенциалов между точками А и В равна 9 В. Имеется два проводника с сопротивлениями 5 Ом и 3 Ом . Найти количество теплоты, выделяющееся в каждом проводнике за единицу времени, если проводники между точками А и В соединены: а) последовательно; б) параллельно.

3.084. ЭДС батареи равна 80 В, внутреннее сопротивление – 5 Ом. Внешняя цепь потребляет мощность 100 ВТ. Определить силу тока в цепи, напряжение под которым находятся внешняя цепь и ее сопротивление.

3.085. Сила тока в цепи изменяется со временем по закону i = I₀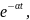 где I₀ = 10A, α = 100 c^-1 . Определить количество теплоты, выделившееся в проводнике за время 0,01 с.

3.086. В проводнике за время 10 с при равномерном возрастании силы тока от 1 А до 2 А выделялось количество теплоты . Найти сопротивление проводника.

3.087. Сила тока в проводнике сопротивлением R = 10 Ом равномерно убывает от значения I_{1 =} 10Адо нуля в течение времени t = 10c. Определить теплоту, выделившуюся за указанный промежуток времени.

3.088. От батареи, ЭДС которой 600 В, требуется передать энергию на расстояние 1 Км. Потребляемая мощность 5 кВт. Найти минимальные потери мощности в сети, если диаметр медных проводящих проводов 0,5 см?

3.089. По проводнику сопротивлением 8 Ом течет равномерно возрастающий ток. За время 8с в проводнике выделилось 500 Дж теплота. Определить заряд, протекающий за это время по проводнику. В момент времени, принятый за начальный, ток в проводнике был равен нулю.

3.090. Какая разность потенциалов получается на зажимах двух элементов, включенных параллельно, если ЭДС соответственно равны 1,4 В и 1,2 В, а внутренние сопротивления равны соответственно 0,6 Ом и 0,4 Ом?

3.091. Два элемента с одинаковыми ЭДС ε₁ =ε₂ =2В и внутренними сопротивлениями r₁ = 1 Ом и r₂ = 2 Ом замкнуты на внешнее сопротивление R(рис. 3.15). Через элемент с ЭДС ε₁ течет ток I₁ = 1A. Найти сопротивление R и ток I₂, текущий через элемент с ЭДС ε₂. Какой ток I течет через сопротивление R?

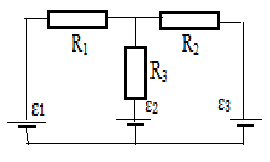
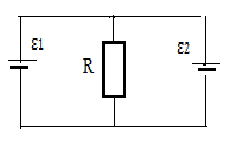
3.092.Батареи имеют ЭДС ε₁= 2B, ε₂= 4B, ε₃= 6B сопротивления R₁ = 4 Ом, R₂ = 6 Ом , R₃ = 8 Ом .(рис. 3.16). Найти токи, текущие во всех участках цепи.

Рис.3.15 Рис.3.16

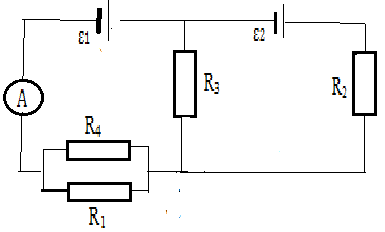
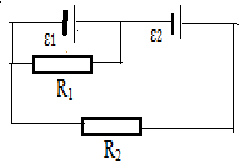
Рис.3.17 Рис.3.18

3.093. Батареи имеют ЭДС ε₁ = ε₂ =100 В сопротивления R₁ = 20 Ом,

R₂ = 10 Ом, R₃ = 40 Ом, R₄ = 30 Ом (рис. 3.17). Найти показания амперметра.

3.094. Батареи имеют ЭДС ε₁ = 2ε₂ сопротивления R₁ = R₃ = 20 Ом, R₂= 15 Ом, R₄ =40 Ом (рис. 3.17). Через амперметр течет ток 1,5 А, направленный снизу вверх. Найти ε₁ и ε₂, а также токи, текущие через сопротивления R₂ и R₃.

3.095. Два одинаковых элемента имеют ЭДС ε_{1 =} ε₂ = 2В и внутренние сопротивления r₁ = r₂ = 0,5 Ом (рис. 3.18). Найти токи, текущие через сопротивления R₁ = 0,5 Ом и R₂ = 1,5 Ом , а также ток через элемент с ЭДС ε₁.

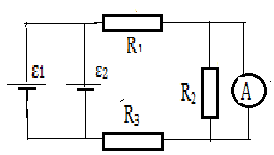
3.096. Элементы имеют ЭДС ε₁ = ε₂ = 1, 5 В и внутренние сопротивления r₁= r₂= 0,5 Ом, сопротивления R₁= R₂ =2 Ом, , R₃ = 1 Ом, сопротивление амперметра R_А = 3 Ом (рис. 3.19). Найти показание амперметра.

Рис. 3.19 Рис.3.20

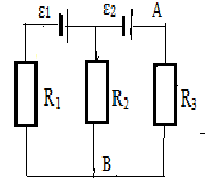
3.097.Вычислить разность потенциалов между точкамиА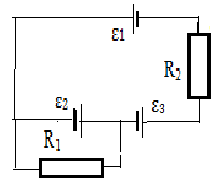 и В в схеме на

рис 3.20, если.ε₁ = 4 В, ε₂ =1В, R₁= R₂= 10 Ом, R₃ =5 Ом

3.098. Найти токи, текущие по каждому сопротивлению

(рис. 3.21), а также напряжение между точками А и В. Поло-

жить: ε₁ = 6 В, ε₂ =5В, ε₃ = 4В_, R₁= 100 Ом. R₂=50 Ом

Рис.3.21

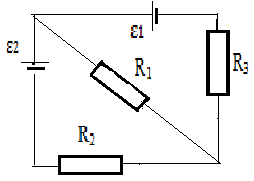
3.099. ЭДС элементов цепи ε₁ = 6 В, ε₂ =5 В, сопротивления R₁=45 Ом, R₂= = R₃ = 10 Ом (рис. 18). Найти токи, текущие во всех участках цепи.

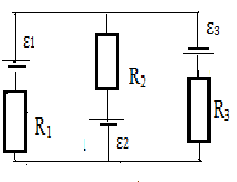
3.100.В схеме на рис.19 ЭДС источников ε₁ =1,5В, ε₂ = ε₃ =2В, и сопротивления R₁= 10 Ом, R₂= 20 Ом, R₃= 30 Ом. Внутренние сопротивления источников пренебрежимо малы. Найти токи, теку-

Рис.3.22 Рис.3.23 щие через резисторы.