Решение.

Величина напряженности электрического поля, созданного в центре квадрата каждым зарядом +q (ε = 1), равна:

E₁ = E₂ = E₃ = E₄ = E = ,

где x =a/√2– расстояние от любой вершины квадрата до его центра.

Для нахождения напряженности, созданной в центре квадрата всеми четырьмя зарядами, воспользуемся принципом суперпозиции (5):

В результате сложения векторов получаем:

E₀ = E –E + E –E = 0

Потенциал электрического поля в центре квадрата находим алгебраическим суммированием

φ₀ = φ_{1 +} φ_{2 +} φ_{3 +} φ₄;

где φ_{1 =} φ_{2 =} φ_{3 =} φ_{4 =} φ = потенциал, созданный каждым зарядом в центре квадрата.

После суммирования окончательно получаем:

φ₀ =

Пример 2.

Протон, летящий к неподвижному ядру двукратно ионизированного атома гелия, на очень большом расстоянии от ядра имеет скорость v₀ =10⁴ м/с. На какое минимальное расстояние протон может приблизиться к ядру?Заряд протона q = e = 1,6∙10^-19 Кл, масса протона m = 1,67∙10^-27 кг.

Решение

В состав ядра атома гелия входят два протона и нейтрона, поэтому ядро гелия можно считать частицей с массой 4m и зарядом q = +2e. Протон, летящий в направлении этого ядра, будет тормозиться электрическим полем ядра до тех пор, пока не остановится на некотором минимальном расстоянии от него. В момент остановки протона расстояние между частицами будет минимальным.

Воспользуемся законом сохранения и превращения энергии

A = W₂ – W₁

где A = q( ) – работа сил электрического поля ядра гелия, совершаемая при торможении протона,

φ₁ - потенциал поля вдали от ядра, где протон обладал кинетической энергией W₁ = ;

φ₂ - потенциал поля ядра, где протон остановился, то есть W₂ = 0.

Обозначим расстояние от ядра до указанных точек поля соответственно R и r. Учитывая, что заряд ядра равен +2e, потенциалы электрического поля в этих точках (ε = 1)равны:

φ₁= и φ₂ = .

При условии R ≫ r работа электрического поля ядра равна:

A = e( = = -

Подставляя выражения для работы сил электрического поля и кинетической энергии протона в исходную формулу закона сохранения и превращения энергии, получаем:

=

Решая это уравнение относительно неизвестного и, подставляя числовые значения, находим:

r = ≅3,45∙10^-10 м

Ответ: r ≅3,45∙10^-10 м

Пример 3.

Шар радиуса R₀ равномерно заряжен с объемной плотностью заряда ρ. Построить графики зависимости E(r) и φ(r), где r– расстояние от центра шара.

Решение

Введем концентрическую с заряженным шаром сферическую поверхность Гаусса радиусом r≤.R₀. В силу сферической симметрии задачи, напряженность одинакова во всех точках поверхности Гаусса и перпендикулярна к ее поверхности. Внутри этой сферы содержится заряд q = ρ

Воспользовавшись теоремой (7), получим:

E∙4πr² = ρ

Отсюда для r≤.R₀ (то есть внутри шара) получаем линейную зависимость напряженности поля от r

E = .

Для определения зависимости напряженности поля вне шара окружим его концентрической сферической поверхностью Гаусса радиусом r > R₀

Напряженность одинакова во всех точках этой поверхности (по модулю) и перпендикулярна к ней. Следовательно, из теоремы (7) следует:

E∙4πr² =

где q = ρ – заряд всего шара.

Отсюда для r > R₀ получаем параболическую зависимость напряженности от r: E =

Учитывая, что напряженность и потенциал в нашем случае связаны соотношением (14 в), вычислим потенциал электрического поля шара в любой точке от его центра:

a) r ≤ R₀

φ = = = =

= = + = ;

б) r > R₀

φ = = = =

ГрафикиE(r ) и φ(r) представлены на рисунках.3.2

:

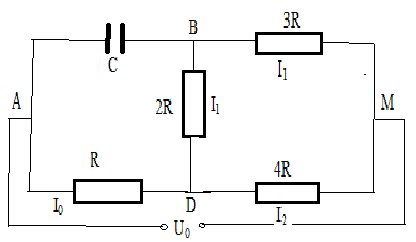
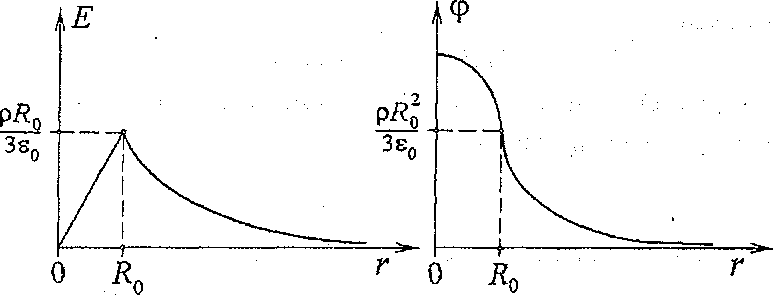
Рис.3.2 Рис.3.3

Пример 4

Найти заряд конденсатора в схеме, изображенной на рисунке рис.3.3.