Филиал ГОУ ВПО "Московский Государственный
Открытый университет"
В г. Кропоткине
Е. П. Рычков
Физика
Методическое пособие
(Сборник задач)
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ К КОНТРОЛЬНЫМ РАБОТАМ ПО ФИЗИКЕ
Кропоткин
2012
УДК…
ББК 22.11я.73
Р93 Автор
Е.П.Рычков – кандидат военных наук доцент кафедры высшей математики и физики филиала МГОУ в г. Кропоткине.
Рецензенты
Г.Г.Гарбуз – кандидат технических наук профессор директор филиала РГУ ПС в г. Кропоткине.
В.П.Шевцов – кандидат технических наук профессор заведующий кафедрой высшей математики и физики филиала МГОУ в г. Кропоткине.
Учебно-методическое пособие рассчитано на студентов технических специальностей ВУЗа. Оно содержит краткие теоретические сведения по базовым разделам курса физики в объемах, необходимых и достаточных для студентов ВУЗа. Приведены основные формулы, примеры решения задач, методические рекомендации решения задач. Задания на контрольные работы представлены сборником задач, заимствованных из различных источников.
Пособие обильно иллюстрировано рисунками (чертежами и схемами).
Печатается по решению Учебно-методического совета филиала МГОУ в г. Кропоткине
ООО "Кавказская типография", 2012 – 118с.
© Е.П.Рычков
©
Филиал ГОУ ВПО "Московский
государственный открытый университет"
в г. Кропоткине.
1 Механика
1.1 Основные понятия, законы и формулы
1.
Мгновенная скорость: vx
=
.
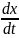2.
Мгновенное ускорение: ах
=
.
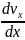3.
Угловая скорость:
.
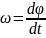4.
Угловое ускорение:
.
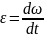5. Связь между линейными и угловыми величинами, характеризующими движение точки по окружности:
v
=
,
=
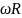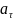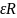, an=co2R
,
где v - линейная скорость;
ах и ап - тангенциальное и нормальное ускорения;
-
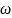угловая
скорость;
-
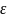угловое
ускорение;
R – радиус окружности.
6.
Полное
ускорение:
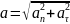
7.
Импульс
материальной точки массой m
, движущейся поступательно со
скоростью
:
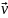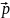= т
.
8.
Второй
закон Ньютона:
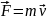и
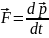
где
-
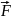результирующая
всех сил, действующих на тело.
9. Силы, рассматриваемые в механике:
9.1.
Сила
упругости:
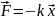и F
= kx,
где k - коэффициент упругости,
х - абсолютная деформация.
9.2.
Сила
тяжести: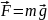
и F=mg,
где g - ускорение свободного падения,
т - масса тела.
9.3.
Сила гравитационного взаимодействия:
F
= G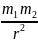
где G — гравитационная постоянная;
т1 и т2 — массы взаимодействующих тел;
r - расстояние между центрами масс тел (тела рассматриваются как материальные точки).
9.4.
Сила трения скольжения: F
=
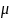N,
где - коэффициент трения;
N - сила нормального давления, прижимающая тело к трущейся поверхности.
10. Закон сохранения импульса (для изолированной системы п - тел):
=
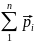const.
11.
Кинетическая
энергия тела, движущегося поступательно:
.
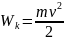где v - скорость тела,
т - масса тела.
12. Потенциальная энергия:
12.1
- упруго деформированной пружины:
.
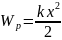где k — жесткость пружины;
x — абсолютная деформация (удлинение);
12.2
- гравитационного взаимодействия:
=
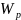G
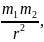
где G — гравитационная постоянная;
т1 и т2 — массы взаимодействующих тел;
r - расстояние между центрами масс тел (тела рассматриваются как материальные точки).
12.3. тела, находящегося в однородном поле силы тяжести:
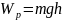
где g -ускорение свободного падения;
h - высота тела над уровнем, принятым за нулевой (формула справедлива при условии h « R, где R - радиус Земли).
13. Модуль момента силы F относительно какой-либо точки "О" равен произведению модуля силы на длину перпендикуляра l (плечо), опущенного из точки "О" на линию действия силы:
M = Fl.
14. Основное уравнение динамики вращательного движения относительно неподвижной оси "О":
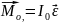
где
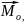- результирующий
момент внешних сил относительно оси
"О", действующих на тело;
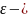угловое ускорение;
I0 -момент инерции тела относительно оси вращения.
15. Момент инерции тел правильной геометрической формы и массы т относительно оси "О", проходящий через центр масс:
15.1. стержня длиной L относительно оси, перпендикулярно стержню:
I0
=
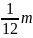L2
15.2. кольца (тонкостенного цилиндра) радиусом R относительно оси, перпендикулярной плоскости кольца (совпадающей с осью цилиндра ):
I0=mR2;
15.3.
диска радиусом R
относительно
оси, перпендикулярной
плоскости
диска I0
=
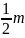R2
15.4. шара радиусом
R:
I0=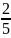
mR2
16. Если известен момент инерции тела относительно оси, проходящей через центр масс тела (I0), то момент инерции относительно произвольной параллельной оси (I) определяется теоремой Штейнера:
I = I0 + md2,
где т - масса тела, d - расстояние между осями.
17.
Момент импульса тела, вращающегося
относительно неподвижной оси "ОО":
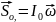
где I0 - момент инерции тела относительно оси "О",
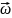- угловая скорость
вращения.
18.
Кинетическая энергия тела, вращающегося
относительно неподвижной оси "О":
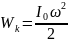
где I0 - момент инерции тела относительно оси "О",
- угловая скорость вращения.
19. Кинематическое уравнение гармонических колебаний материальной точки:
х= Acos{
t
+
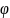0),
где х - смещение;
А - амплитуда колебаний;
- циклическая (круговая) частота;
0 - начальная фаза.
20. Скорость и ускорение материальной точки, совершающей гармонические колебания:
v
=
-
A
sin{
t
+
0),
a
=
-A
2
cos
t
+
0).
21. Период колебаний физического маятника:
T=2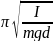
где I -момент инерции маятника относительно его оси вращения;
т - масса маятника;
g - ускорение свободного падения;
d - расстояние от центра масс до оси вращения.