§4. Понятие дифференцируемости функции нескольких переменных.

Пусть функция y = f(X) определена в точке M(X) и в некоторой ее окрестности. Составим полное приращение функции в точке М(Х)= M(x₁, x₂, . . . , x_n). Для этого дадим приращения каждой независимой переменной DМ(Dх₁, Dx₂, . . . , Dx_n). В результате получим «новую» точку М + DМ = (x₁+Dx₁, x₂+Dx₂, . . . , x_n+Dx_n), которая принадлежит данной окрестности точки М. Тогда полным приращением Dy функции y = f(X) в точке M(X) будет являться разность:

Dy = f(M+DM) – f(M) = f(x₁+Dx₁, x₂+Dx₂, . . . , x_n+Dx_n) - f(x₁, x₂, . . . , x_n) (1).

Определение. Функция y = f(X) называется дифференцируемой в точке M(X), если ее полное приращение (1) в этой точке можно представить в виде:

Dy = + +. . .+ +a₁Dx₁+a₂Dx₂+ . . .+ a_nDx_n (2),

где a₁, a₂, . . . a_n – бесконечно малые функции соответственно при Dx₁ ® 0, Dx₂ ® 0, . . . Dx_n ® 0.

Сумма первых n слагаемых в равенстве (2) представляет собой линейное выражение относительно Dx₁, Dx₂, . . . , Dx_n и является главной линейной частью полного приращения функции y = f(X), которое называется полным дифференциалом этой функции и обозначается dy или df(X):

dy = = + +. . .+ (3).

Для независимых переменных x₁, x₂, . . . , x_n полагают Dx₁ = dx₁, Dx₂ = dx₂, . . . , Dx_n = dx_n, тогда формулу (3) можно переписать в виде:

dy = = + +. . .+ (4).

Теорема 1. (необходимое условие дифференцируемости функции)

Если функция y = f(X) дифференцируема в точке M(X), то она непрерывна в этой точке и имеет в ней частные производные , i = 1,2,…n.

Доказательство.

Пусть выполняется условие (2) и - некоторые числа (i = 1,2,…n).

Из условия (2) следует, что частные приращения функции y = f(X) в точке М, соответствующие приращению Dх_i любого из n аргументов x_i, i = 1,2,…n, будут иметь вид:

D_хiy = + a_iDx_i, т.к. Dx_i ¹ 0, а все Dx_j = 0, если j ¹ i.

Тогда . Устремим Dx_i ®0 и перейдем к пределу

, т.к. 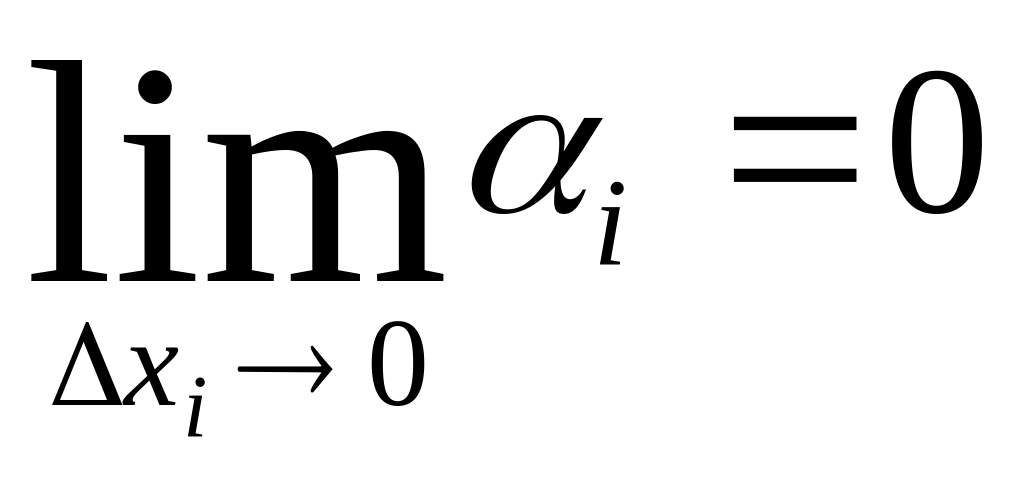по определению (2).

Непрерывность функции f(X) в точке М следует непосредственно из условия (2):

т.е. Dy ® 0 при Dx_i ® 0, i = 1,2, . . . , n. Ч.т.д.

Теорема 2. (достаточное условие дифференцируемости функции)

Если функция y = f(X) имеет частные производные по всем аргументам в некоторой окрестности точки М(Х), причем эти производные непрерывны в самой точке М(Х), то данная функция дифференцируема в точке М(Х). (без доказательства).

Теорема 2 имеет важное следствие: непрерывность функции вытекает из непрерывности ее частных производных.

Непрерывность функции нескольких переменных напрямую проверить бывает довольно сложно, но, используя данное следствие, можно установить это свойство функции, если проверить непрерывность ее частных производных.

Замена факторов по функции Кобба-Дугласа.

Установим, на какую величину следует изменить объем вложенного капитала K, чтобы при изменении трудовых ресурсов на DL выпуск продукции оставался неизменным.

Функция Кобба-Дугласа: Q = AK^aL^1-a.

dQ = = + .

Полагая Q (выпуск) неизменным (const) получаем, что дифференциал этой функции равен 0, т.е. dQ = 0 или + =0 Þ .

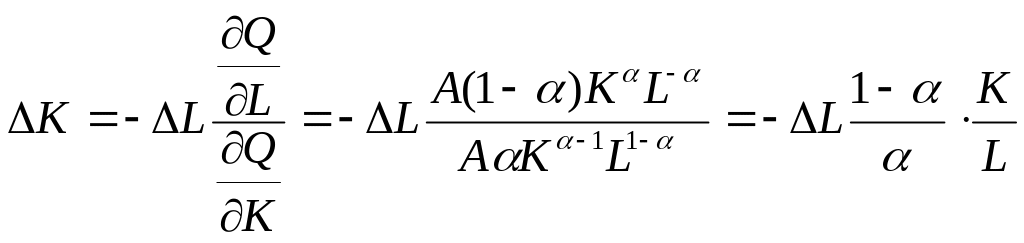Итак (5)

или в относительных величинах: , что означает:

если ресурс труда изменится (например, увеличится) на 1%, то ресурс капитала следует изменить (уменьшить) на % для того, чтобы выпуск продукции остался неизменным.

Из (5) следует формула - предельная норма замены трудовых ресурсов L капиталом K.