Пример 9

Р ис 9. Блок-схема алгоритма прочности таврового сечения при действии изгибающего момента для расположения нейтральной оси в ребре (метод предельных усилий)

Рис 10. Блок-схема алгоритма расчета площади поперечного сечения продольной арматуры железобетонных элементов таврового профиля при действии изгибающего момента для случая расположения

нейтральной оси в полке

Р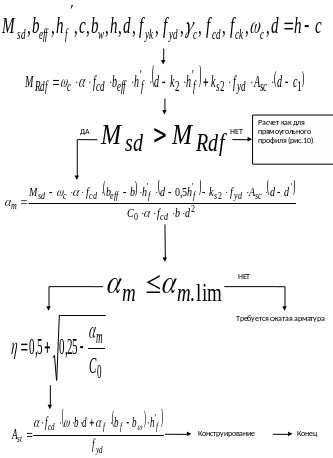 ис.11. Блок-схема подбора арматуры в тавровом сечении при расположении нейтральной оси в ребре

Решение:

(алгоритм расчета по блок-схеме рис.8)

1. Положение границы сжатой зоны

=1·13,33·300·100=399900Н=399,9кН - продольная сила, воспринимаемая полкой таврового сечения

=417·982=409494Н=409,49кН - продольная сила, воспринимаемая арматурой

Так как N_f =399.9кН<Ns=409.49кН – граница сжатой зоны находится в ребре и расчет ведется как для таврового сечения.

2. Определяем d=h-c=600-50=550 мм

3.Расчетная высота сжатой зоны

мм

4. Относительная высота сжатой зоны:

5. Граничная относительная высота сжатой зоны:

где ω=k_c-0.008·f_cd=0.85-0.008*13.33=0.74

k_c=0.85 для тяжелого бетона

6. Сравниваем значения относительной высоты сжатой зоны с граничной

Т.к. ξ<ξ_lim определяем предельный момент, воспринимаемый сечением по формуле:

7. M_Rd=250 кН·м >M_sd=200 кН·м,

7. Прочность сечения обеспечена.

Пример 10

Дано: Тавровое сечение с размерами = 300 мм, bw=150 мм , =150 мм , h = 600 мм, с = 50 мм. Бетон класса С20/25 (fck = 20 МПа, gс = 1,5, fcd = fck/gc = 20/1,5 = 13,33 МПа). Растянутая арматура класса S500 (fyk = 500 МПа, fyd = 417 МПа, Es = 20×104 МПа), Ast = 982 мм2 (2Æ25 S500). Изгибающий момент MSd = 200 кН×м. Требуется: Проверить прочность сечения.

Решение:

(алгоритм расчета по блок-схеме рис.9)

1. Положение границы сжатой зоны

=1·13,33·300·150=599849Н=599,8кН - продольная сила, воспринимаемая полкой таврового сечения

=417·982=409494Н=409,5 кН - продольная сила, воспринимаемая арматурой

Так как N_f=599,8кН>N_s=409.5кН – граница сжатой зоны находится в полке и расчет ведется как для прямоугольного сечения шириной b`_f = 300 мм.

2. Определяем d=h-c=600-50=550 мм

3. Высота сжатой зоны:

мм

4. Относительная высота сжатой зоны:

5. Граничная относительная высота сжатой зоны:

где ω=k_c-0.008·f_cd=0.85-0.008*13.33=0.74

k_c=0.85 для тяжелого бетона

6. Сравниваем значения относительной высоты сжатой зоны с граничной

Т.к. ξ=0.186<ξ_lim=0.581 определяем предельный момент, воспринимаемый сечением по формуле:

7. M_Rd=204.25 кН·м >M_sd=200 кН·м, следовательно прочность сечения обеспечена.