2.4 Практическое применение законов распределения размеров для анализа точности обработки

Законы распределения размеров используются в технологии машиностроения для установления надежности проектируемого технологического процесса.

Надежность обеспечения требуемой точности обработки заготовок характеризуется запасом точности  данной операции, который определяется по формуле

( 2.2 )

где IТ – допуск на обработку;

 - фактическое поле рассеяния размеров заготовок.

Величина поля рассеяния  при различных законах распределения обрабатываемых заготовок определяется.

Нормальное распределение (закон Гаусса): 6 σ, 4,9 σ, 3,46 σ.

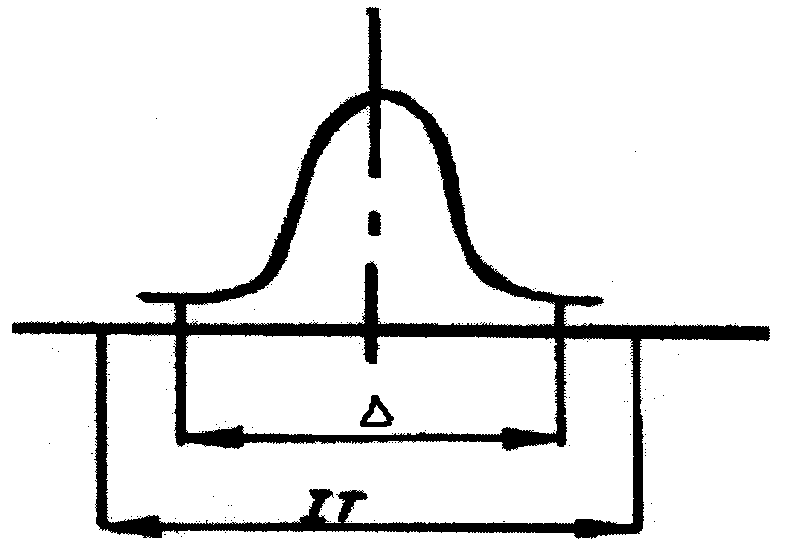
Рисунок 2.2 – Нормальное распределение (закон Гаусса) 6 σ

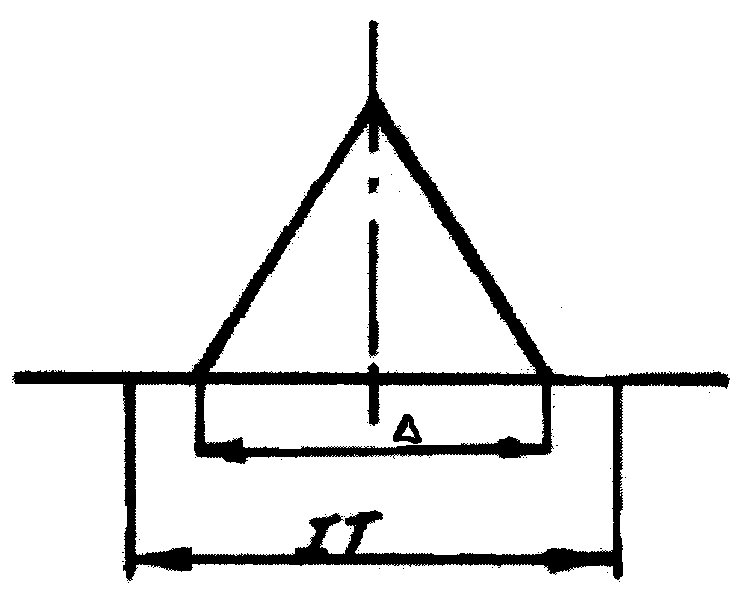
Рисунок 2.3 – Закон Симпсона 4,9

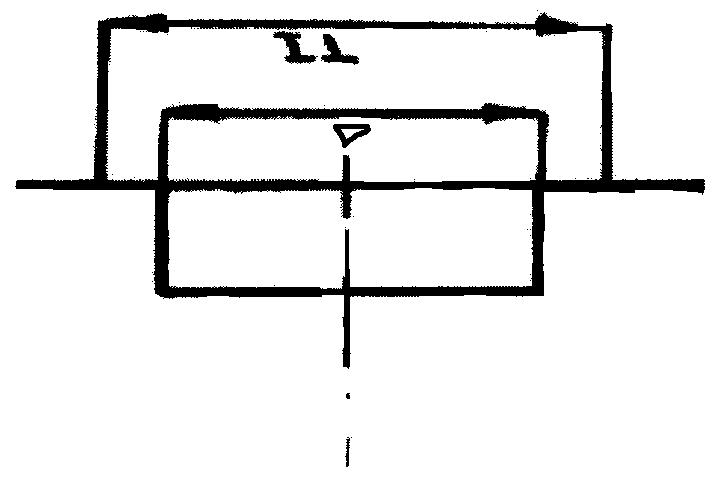
Рисунок 2.4 – Закон равной вероятности 3,46

Когда запас точности  > 1,0, обработка заготовок может быть осуществима без брака, если правильно настроена система. При  < 1,0 брак заготовок является весьма вероятным.

При   1,2 процесс обработки считается надежным. Для всех законов распределения размеров условием обработки заготовок без брака является выражение  < IТ, т.е. фактическое поле рассеяния размеров должно быть меньше допуска на обработку, для нормального закона это выражение приобретает вид 6 < IТ.

2.5 Анализ параметров качества изделий методами математической статистики

Как показывает практика, изготовление деталей при помощи даже одного и того же технологического процесса ведет к неизбежному рассеиванию размеров в результате совместного действия различных факторов. Если мы будем измерять размеры деталей, обрабатываемых при одном и том же положении режущего инструмента относительно детали или при использовании для обработки одного и того же мерного инструмента, то увидим, что полученные размеры неодинаковы, они имеют различные по величине отклонения от номинального размера.

Многочисленные исследования показывают, что факторы, вызывающие погрешности обработки, влияют на точность размера с определенной закономерностью, т.е. возникающие погрешности изменяются по определенным законам распределения. Знание закона изменения этих погрешностей позволяет принимать меры для их устранения или уменьшения их влияния на точность при построении станочных операций.

Что же собой представляет закон распределения случайной величины?

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения характеризуется рядом признаков, некоторые характерные из них приводятся ниже

( 2.3 )

где n – вероятность значения случайной величины;

N – частота.

1. Ряд распределения случайной величины - это таблица, где перечислены возможные (различные) значения этой величины с соответствующими им вероятностями.

2. Функция распределения случайной величины - это математическое выражение вероятности того, что случайная величина принимает определенное значение.

3. Поле рассеяния - это разность между наибольшим и наименьшим значениями исследуемой величины.

4. Математическое ожидание – это среднее значение случайной величины, определенное по формуле

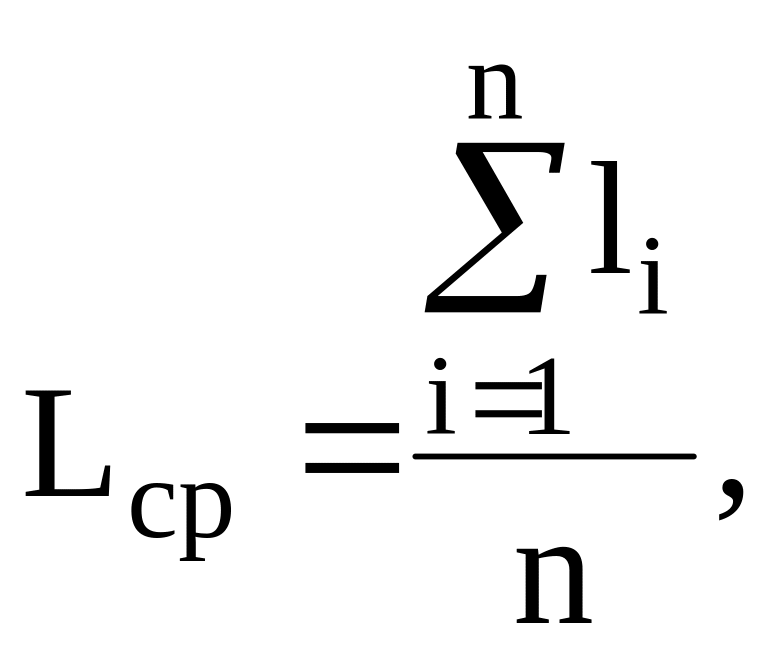( 2.4 )

5. Среднее квадратичное отклонение определяется по формуле

( 2.5 )

где l_i – текущий размер исследуемой величины;

L_ср – среднее арифметическое значение или математическое ожидание;

n – количество измерений или наблюдений.

Наиболее чаще применяется закон нормального распределения (закон Гаусса) для оценки точности отдельных операций или всего технологического процесса. Нормальный закон распределения имеет место, когда исследуемая случайная величина является результатом действия большого числа различных факторов.