9.Свободное движения точки . Основные понятие .Закон скорости и ускорения .

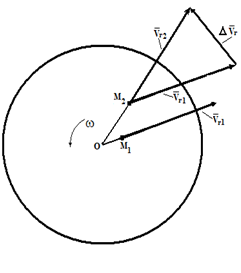
Движение свободного тв.тела (общий случай движения). Свободное тв.тело имеет шесть степеней свободы. При рассмотрении движения св.тв.тела, кроме неподвижной системы координат Oxyz, вводится подвижная система координат Ax1y1z1, которая связана с телом в точке А. Тогда движ. св.тв.тела представляет собой сложное движение, которое можно рассматривать как состоящее из поступательного движения вместе с полюсом (А) и сферич. движ. вокруг полюса. Ур-ия движ.св.тв.тела: xA=f1(t); yA=f2(t); zA=f3(t); Y=f4(t); q=f5(t); j=f6(t) (углы Эйлера). Первые три ур-ия определяют поступательную часть движ. и зависят от выбора полюса, остальные три определяют сферич. движ. вокруг полюса и от выбора полюса не зависят. Скорость любой точки св.тв.тела = геометрической сумме скорости полюса и скорости этой точки в ее сферическом движении вокруг полюса.  Ускорение точки св.тв.тела = геометрической сумме ускорения полюса, осестремительного ускорения точки и ее вращательного ускорения, определенных относительно мгновенной оси и оси углового ускорения, проходящих через полюс., два последних члена дают ускорение точки в ее движении вокруг полюса.

10.Сложное движение точки. Закон скорости и ускорения .Ускорение Кориолиса .

В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух системах отсчета (далее СО)

Согласно теореме Кориолиса, абсолютное ускорение точки в сложном движении определяется как геометрическая сумма относительного, переносного и кориолисова ускорений (рис. 3) 

                                        a_a = a_r  ⊕   a_e  ⊕  a_C   .

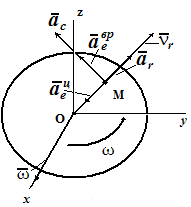 Поскольку, в данном случае, относительное движение происходит по прямой линии, относительное ускорение a_r  направлено вдоль этой прямой и определяется выражением

    Переносным ускорением точки M является ускорение точки M диска. Диск совершает вращательное движение, следовательно, переносное ускорение определяется выражением

  a_e = a_e^вр  ⊕  a_e^цс            ,

где  a_e^вр= ε⋅ OM  - вращательное ускорение точки M, направленное перпендикулярно отрезку OM ;

       a_e^цс= ω²⋅ OM - центростремительное ускорение точки M, направленное к центру диска.

    Ускорение Кориолиса или поворотное ускорение определяется по формуле

a_C = 2 ω_e  ⊗  ν_r          ,

 где  ω_e - переносная угловая скорость,

        ν_r  - относительная скорость точки.

    Направление ускорения Кориолиса определяется по правилу векторного произведения или по правилу Жуковского.

    Величина ускорения Кориолиса определяется выражением

         a_C = 2 ω_e  ν_r  sinα      ,

где  α  – угол между векторами ω_e  и ν_r  .

    Рассмотрим, какой физический смысл заложен в ускорение Кориолиса. Для простоты будем считать, что диск вращается с постоянной угловой скоростью, а точка M движется относительно диска с постоянной относительной скоростью (рис.4).