(Q1x1)(q2x2)...(Qnxn)m, где m есть кнф.

Положим Q_r есть квантор существования в префиксе (Q₁x₁)(Q₂x₂)...(Q_nx_n), . Тогда алгоритм перехода от ПНФ к ССФ описывается следующей последовательностью шагов:

1. Если никакой квантор не стоит в префиксе левее Q_r, выбираем новую константу с, отличную от других констант, входящих в М, заменяем все вхождения x_r, встречающиеся в М, на с и вычеркиваем (Q_rx_r) из префикса.

2. Если Q_{s ...} Q_s - список всех кванторов , встречающихся левее Q_r, , выбираем новый m-местный функциональный символ f, отличный от других функциональных символов, заменяем все x_r в М на 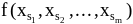и вычеркиваем (Q_rx_r) из префикса.

3. Шаги 1 и 2 применяем ко всем кванторам в префиксе. Последняя из полученных формул есть скулемовская стандартная форма или просто стандартная форма формулы F. Константы и функции, используемые для замены переменных квантора существования, называются скулемовскими функциями.

Необходимо также знать следующие определения. Дизъюнкт есть дизъюнкция литер. Иногда в целях удобства дизъюнкт обозначают как множество литер. Например, . Дизъюнкт, содержащий r литер, называется r-литерным дизъюнктом. Однолитерный дизъюнкт называется единичным дизъюнктом. Дизъюнкт не содержащий никаких литер, называется пустым дизъюнктом. Пустой дизъюнкт всегда ложен, будем обозначать его Л. Считают, что множество дизъюнктов S есть конъюнкция всех дизъюнктов из S, где каждая переменная в S считается управляемой квантором всеобщности. Благодаря этому соглашению ССФ может быть просто представлена множеством дизъюнктов. Ранее упоминалось, что можно элиминировать (устранить) кванторы существования, сохраняя противоречивость формулы. Это утверждение доказывается в следующей теореме.

Теорема 3. Пусть S - множество дизъюнктов, которые представляют ССФ формулы F. Тогда F противоречива в том и только в том случае, когда S противоречива. Необходимо знать доказательство этой теоремы (см.[7,с.55-58]). Отметим, что формула может иметь более чем одну стандартную форму. Для простоты при преобразовании формулы F в стандартную форму S стараются заменять кванторы скулемовскими функциями настолько простыми, насколько возможно. Тогда для формулы можно отдельно получить множество дизъюнктов S_i, где каждый S_i представляет стандартную форму F_i, i=1,...,n. Затем допускаем, что . Опираясь на теорему 3, можно доказать что F противоречива тогда и только тогда, когда S противоречива. В дальнейшем для доказательства теорем будем использовать процедуру опровержения. На входе процедуры опровержения всегда стоит множество дизъюнктов S. Для множества дизъюнктов используют термины “невыполнимо” (“выполнимо”) вместо “противоречиво” (“непротиворечиво”).

Одной из наиболее эффективных процедур поиска опровержения формулы является метод резолюций. Основная идея метода резолюций состоит в том, чтобы проверить, содержит ли S пустой дизъюнкт Л. Если S содержит Л, то S невыполнимо. Если S не содержит Л, то проверяется следующий факт: можно ли получить Л из S. Действительно, множество дизъюнктов невыполнимо тогда и только тогда, когда пустой дизъюнкт Л является логическим следствием этого множества:

Л,

(Выражения обозначают соответственно “А дает В”; “А тогда и только тогда, когда В”). Таким образом, невыполнимость множества дизъюнктов S можно доказать порождением логических выводов из S до тех пор, пока не получим пустой дизъюнкт Л.

Для порождения логических следствий используется такая схема. Пусть A, B, X - формулы и пусть и истинны одновременно. Тогда имеем: если X истинно, то В также должно быть истинным. Если Х ложно, то обязательно А истинно, т.е. формула обязательно истинна. Тогда выполняется следующее правило:

.

Это правило можно записать иначе:

,

где Х-высказывание, представленное литерой в логике высказываний или предикатным символом; А и В - дизъюнкты. Данное правило известно как правило резолюций. Справедливость его можно установить, например, воспользовавшись Теоремой 1, т.е.

Если , то И.

Имеет место Лемма 1: Пусть S₁ и S₂ - дизъюнкты некоторой КНФ, обозначенной S, и пусть L-литера. Если , то дизъюнкт

является логическим следствием нормальной формы S.

Следствие Леммы 1: Нормальная форма S и формула эквивалентны. Дизъюнкт r называется резольвентой дизъюнктов S₁ и S₂. Литеры L и называются контрарными.

Обобщенный алгоритм доказательства невыполнимости конечного множества дизъюнктов S, при условии, что Л состоит из последовательности шагов:

1. Выбираем дизъюнкты S₁, S₂ и литеру L такую, что , и получаем резольвенту r.

2. Добавляем r в множество S и получаем

1. .

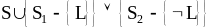Шаги (1) и (2) повторяются до тех пор, пока не будет получен пустой дизъюнкт Л.

Необходимо знать следующие определения. Пусть S-множество дизъюнктов. Резолютивный вывод C из S есть такая конечная последовательность C₁, C₂,..., C_k дизъюнктов, что каждый C_i или принадлежит S или является резольвентой дизъюнктов, предшествующих C_i, и C_k = C. Вывод Л из S называется опровержением (или доказательством невыполнимости) S.

При использовании метода резолюций для логики первого порядка необходимо обратить внимание на следующие особенности. Существенным моментом в применении правила резолюции является нахождение в дизъюнкте литеры, которая контрарна литере в другом дизъюнкте. Для дизъюнктов, не содержащих переменных, это просто. Если же дизъюнкты содержат переменные, процедура доказательства усложняется. В этом случае предварительно должна быть проведена некоторая подстановка в переменные и введено понятие унификации с помощью этой подстановки. Например, рассмотрим предикаты L(x) и L(a), где x -переменная, a - константа. В этих предикатах предикатные символы одинаковы, чего нельзя сказать о самих предикатах. Тем не менее, подстановкой a в x можно эти предикаты сделать одинаковыми (эта подстановка называется унификацией). Целью унификации является обеспечение возможности применения алгоритма доказательства методом резолюций для предикатов. Например, если имеем:

то предикаты L(x) и не являются контрарными. При подстановке a вместо x получим L(a) и , т.е. контрарную пару. Подстановку t в x принято записывать {t|x}. В общем случае подстановка - это конечное множество вида {t₁|v₁, t₂|v₂, ... , t_n|v_n}, где каждое v_i - переменная, каждое t_i - терм (константа, переменная, символ функции), отличный от v_i, причем все v_i разные.

Пусть ={t₁|v₁, t₂|v₂, ... , t_n|v_n} - подстановка, E - выражение. Тогда E - выражение, полученное из E заменой одновременно всех вхождений переменной v_i ( ) в E на терм t_i, E называется примером E.

Например, пусть  ={a|x, f(b)|y, c|z} и E=P(x, y, z). Тогда E =P(a, f(b), c). Подстановка  называется унификатором для множества {E₁,E₂,...,E_k} тогда и только тогда, когда E₁=E₂=...= E_k. Говорят, что множество {E₁,...,E_k} унифицируемо, если для него существует унификатор. Например, множество {P(a, y), P(x, f(b))} унифицируемо, т.к. подстановка ={a|x, f(b)|y} является его унификатором.

Рассмотрим примеры решения типичных упражнений и задач:

1. Получить ССФ формулы (x)(y)(z)(u)(v)(w)P(x,y,z,u,v,w).

Решение. Данная формула находится в предваренной нормальной форме. Воспользуемся алгоритмом перехода от ПНФ к скулемовской стандартной форме. В данной формуле левее (x) нет никаких кванторов всеобщности, левее (u) стоят (y) и (z), а левее (w) стоят (y), (z) и (v). Следовательно, мы можем заменить переменную x на константу a, переменную u  на двухместную функцию f(y,z), переменную w  на трехместную функцию g(y,z,v). Таким образом, получаем следующую стандартную форму для заданной формулы:

(y)(z)(v)P(a,y,z,f(y,z),g(y,z,v)).

2. Получить ССФ для формулы

(x)(y)(z)((P(x,y)Q(x,z))R(x,y,z)).

Решение. Сначала приведем матрицу к КНФ:

(x)(y)(z)((P(x,y)R(x,y,z))(Q(x,z)R(x,y,z))).

Затем, т.к. перед (y) и (z) есть (x), то переменные y и z заменяются соответственно одноместными функциями f(x) и g(x). Таким образом, получаем следующую ССФ:

(x)((P(x,f(x))R(x,f(x),g(x)))(Q(x,g(x))R(x,f(x),g(x)))).

3. Пусть S  ССФ формулы F. Если F противоречива, то по Теореме 3 F=S. Если F непротиворечива, то, вообще говоря, F не эквивалентна S. Доказать это утверждение.

Доказательство. Пусть, например, . Ясно, что S есть стандартная форма формулы F. Выберем интерпретацию I следующим образом:

Область: D={1,2}.

Значения для a:

a

1

Значения для P:

P(1)	P(2)
0	1

Тогда ясно, что F истинна в I, поскольку P(x)   (x)P(x)=1. Однако S ложна в I, поскольку a=1P(a)=P(1)=0. Таким образом, FS.