2.2. Система «Минимум-максимум»

Эта система, как и система с установленной периодичностью пополнения запасов до постоянного уровня, содержит в себе эле­менты основных систем управления запасами. Как и в системе с фиксированным интервалом времени между заказами, здесь исполь­зуется постоянный интервал времени между заказами. Система «Ми­нимум-максимум» ориентирована на ситуацию, когда затраты на учет запасов и издержки на оформление заказа настолько значительны, что становятся соизмеримы с потерями от дефицита запа­сов. Поэтому в рассматриваемой системе заказы производятся не через каждый заданный интервал времени, а только при условии, что запасы на складе в этот момент оказались равными или меньше установленного минимального уровня. В случае выдачи заказа его размер рассчитывается так, чтобы поставка пополнила запасы до максимального желательного уровня. Таким образом, данная систе­ма работает лишь с двумя уровнями запасов - минимальным и максимальным, чему она и обязана своим названием.

Исходные данные для расчета параметров системы таковы:

• потребность в заказываемом продукте, шт.,

• интервал времени между заказами, дни,

• время поставки, дни,

• возможная задержка поставки, дни.

В системе «Минимум - максимум» существуют показатели, которые рассчитываются таким же образом, как и в системе с фиксированным размером заказа. К таким показателям относятся:

• ожидаемое дневное потребление (см. формулу 6);

• ожидаемое потребление за время поставки (см. формулу 8);

• Максимальное потребление за время поставки (см. формулу 9);

• Гарантийный запас (см. формулу 10).

• пороговый уровень запаса (см. формулу 11).

Максимальный желательный запас в системе «Минимум - максимум» рассчитывается по формуле (17) приведенной выше.

А расчет размера заказа в рассматриваемой системе производится по формуле (18) также приведенной выше.

Для определения интервала времени между заказами следует воспользоваться формулой (14) и комментариями к ней.

Гарантийный (страховой) запас позволяет обеспечивать потреби­теля в случае предполагаемой задержки поставки. Как и система с установленной периодичностью пополнения запасов до постоянно­го уровня, гарантийный запас используется для расчета порогового уровня запаса.

Пороговый уровень запаса в системе «Минимум - максимум» вы­полняет роль «минимального» уровня. Если в установленный мо­мент времени этот уровень пройден, т. е. наличный запас равен пороговому уровню, или не достигает его, то заказ оформляется. В противном случае заказ не выдается, и отслеживание порогового уровня, а также выдача заказа будут произведены только через за­данный интервал времени.

Максимальный желательный запас в системе «Минимум - макси­мум» выполняет роль «максимального» уровня. Его размер учитыва­ется при определении размера заказа. Он косвенно (через интервал времени между заказами) связан с наиболее рациональной загруз­кой площадей склада при учете возможных сбоев поставки и необ­ходимости бесперебойного снабжения потребления.

Постоянно рассчитываемым параметром системы «Минимум - максимум» является размер заказа. Как и в предыдущих системах управления запасами, его вычисление основывается на прогнозируемом уровне потребления до момента поступления заказа на склад организации. Расчет размера заказа производится по формуле (18).

Г рафическая иллюстрация функционирования системы управления запасами «Минимум - максимум» приведена на рис. 5

Рис. 5. График движения запасов в системе управления запасами

«Минимум - максимум»

Условные обозначения:

х - момент заказа; - время поставки; - время задержки поставки.

Примеры. Суммарные годовые затраты С:

,

где С₀ – затраты на выполнение заказа (на поставку продукции и т.п.), ден.ед.;

S – годовой спрос или годовое потребление, ед.;

С₁ – цена единицы закупаемой продукции, ден.ед.;

i – годовые затраты на содержание (хранение) единицы продукции,;

q₀ – количество единиц продукции, содержащихся в одной закупаемой партии.

1. Оптимальный размер закупаемой партии при мгновенном пополнении заказа:

.

Графическое определение оптимального размера закупаемой партии показано на рис. 6.

Существуют формулы расчета оптимального размера партии.

2. Оптимальный размер производимой партии:

,

где р - годовое производство запасов.

Рис. 6. Графическое определение оптимального размера

закупаемой партии.

4. Определение оптимального размера партии при допущении дефицита:

h - издержки или штрафные потери, обусловленные дефици­том и отнесенные к единице продукции за единицу времени;

T_y - общее время цикла.

Оптимальный размер партии при наличии дефицита равен:

.

Максимальный запас при дефиците:

.

Общее время цикла

.

Пример 1:

Известны следующие данные: затраты на поставку единицы продукции С₀ = 12,75 ден.ед.; годовое потребление S = 1000 ед.; годовые затраты на хранение продукции i = 0,1 ден.ед.; размер партии поставки: годовое производство q – 100, 200, 400, 500, 600, 800, 1000 ед.; годовое производство р = 12000 ед.; издержки, обусловленные дефицитом h = 0,2 ден.ед.

Необходимо:

1) Рассчитать оптимальный размер закупаемой партии и построить график.

2) Определить оптимальный размер закупаемой партии при пополнении запаса за конечный интервал.

3) Рассчитать оптимальный размер партии в условиях дефицита.

Решение.

1. Закупаемая партия может быть рассчитана по формуле (5):

= ед.

Для определения оптимального размера закупаемой партии составим таблицу:

Размер партии	100	200	400	500	600	800	1000
Издержки выполнения заказа, ден.ед.	127,5	63,75	31,87	25,5	21,25	15,9	12,75
Издержки хранения, ден.ед.	5,0	10,0	20,0	25,0	30,0	40,0	50,0
Суммарные годовые издержки, ден.ед.	132,5	73,75	51,87	45,5	51,25	55,9	62,75

Построим график:

Рис. 7. Определение оптимального размера закупаемой партии.

2. Определим оптимальный размер закупаемой партии при пополнении запас за конечный интервал q_m :

ед.

3. определим оптимальный размер партии в условиях дефицита:

ед.

Максимальный положительный запас при наличии дефицита:

ед.

Общее время цикла:

.

Приведенные расчеты показали, что при дефиците увеличиваются оптимальный размер партии (613 вместо 500 ед.) и промежуток времени между точками заказов (0,61 вместо 0,50 = 500/1000).

Пример 2: Известно, что годовой спрос S составляет 1000 ед.: затраты, связанные с доставкой продукции А, - 20,0 ден.ед.; цена единицы продукции – 1,4 ден.ед.; затраты на содержание запасов – 40% цены единицы продукции.

Необходимо определить:

1. Оптимальный размер партии поставки.

2. Какую цену должен установить продавец при поставке продукции партиями по 450 ед.?

3. Каков будет оптимальный размер поставки при производстве продукции на собственном предприятии в количестве 150 000 ед. в год?

Решение.

1. Затраты на содержание запасов от цены единицы продукции, если известно, что они составляют 40%:

i = C₁*40% = 0.4*4 = 0.96 ден.ед.

Оптимальный размер партии поставки:

ед.

2. Цена определяется из затрат на содержание запаса, т.е.

;

i – определяем по формуле:

,

если мы возведем формулу в квадрат, то получим:

,

откуда

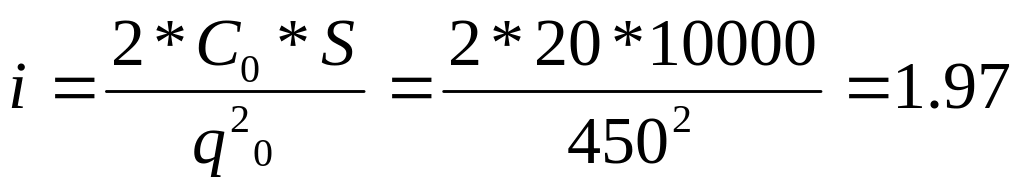ден.ед.;

ден.ед.

Каков будет оптимальный размер при производстве продукции на собственном предприятии в количестве 150 000 ед. в год?

Используем формулу:

ед.

где р – годовое производство.