3.5 Сетевая модель технологического процесса
Сетевая модель описывает множество структур технологического процесса, отличающихся количеством и (или) составом элементов структуры при неизменном отношении порядка.
Структура элементов сетевой модели описывается ориентированным графом, не имеющим ориентированных циклов. В модели может содержаться несколько вариантов проектируемого технологического процесса, однако во всех вариантах порядок элементов одинаков.
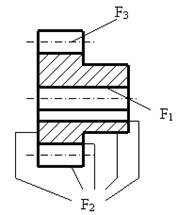
Рисунок 5 – Эскиз детали «Зубчатое колесо
Рассмотрим сетевую модель технологического проектирования маршрута обработки детали «Зубчатое колесо», эскиз которой представлен на рис.5.
Первоначально рассмотрим граф взаимосвязи операторов (технологических операций) по возможной последовательности их выполнения изображенный на рисунке 6.
Рисунок 6. Граф взаимосвязи операторов (технологических операций) по возможной последовательности их выполнения
Кроме данного графа сетевая модель включает в себя таблицу связей свойств поверхностей детали и операторов технологического процесса (в этом примере – технологических операций) – табл.3.
Таблица 3 - Связи между свойствами поверхностей детали и операторами технологического процесса
3.6 Перестановочная модель технологического процесса
Перестановочная модель описывает множество структур технологического процесса, отличающихся количеством и (или) составом элементов структуры при изменении отношения порядка.
Отношения порядка в этих моделях задаются с помощью графа, содержащего ориентированные циклы.
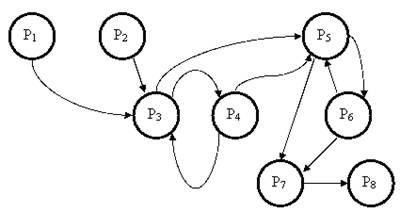
Рисунок 7 – Граф расцеховки
На рисунке 7 обозначены через P1, P2,…, P8 цеха различного назначени:.
P1 – литейный;
P2 – кузнечный;
P3 – механический;
P4 – термический;
P5 – механосборочный;
P6 - общей сборки;
P7 – испытательный;
P8 – упаковочный.
Сетевые и перестановочные модели используют для получения типовых, групповых и индивидуальных технологических процессов. Наличие в них вариантов позволяет производить оптимизацию технологических процессов.
Характерным примерами функциональных моделей являются математические модели, используемые при расчете и оптимизации режимов резания.
Тема 4. Автоматизация проектирования технологических процессов
4.1 Принципы автоматизации процесса принятия решения.
Технологическое проектирование есть последовательный процесс принятий решений по отдельным частным технологическим задачам. Причем по каждой задаче, за исключением задач расчетного характера, решение принимают в результате выбора из известных типовых решений с учетом комплекса условий. Такое представление процесса технологического проектирования указывает путь для формализации самого процесса принятия решений. Для этого достаточно описать каким-либо образом весь набор типовых решений, а также условий, при которых может быть применено каждое из них. Тогда процесс выбора сведется к проверке соответствия исходных данных условиям применимости типовых решений; при выполнении всех условий комплекса принимают соответствующее типовое решение.
Рассмотрим задачу назначения станка на операцию зубо-шевингования. В соответствии со сформулированным выше принципом решения нерасчетных задач в первую очередь необходимо выявить множество типовых решений (МТР). Допустим, на предприятии имеются зубошевинговальные станки трех моделей, они и составят это множество: МТР = {5А702Г; 5703В; 5717С}.
Сформируем
комплекс условий применимости выявленных
типовых решений. Естественными условиями
применимости в данном случае являются
размещаемость детали в рабочей зоне
станка и возможность обработки ее на
станке данной модели. Первая группа
условий регламентирует габаритные
размеры детали (диаметр шестерни D
и длину L),
которые должны находиться в пределах
допустимых рабочей зоной станка. Вторая
группа условий определяет диапазоны
допустимого изменения таких параметров,
как модуль и угол наклона зуба.
Математически все перечисленные условия
выбора модели зубошевинговального
Станка можно описать в виде двойных
неравенств. Следовательно, комплекс
условий применимости (КУП) в рассматриваемой
задаче может быть представлен в виде
системы из известных типовых реше-
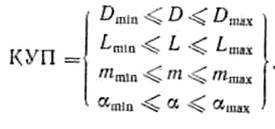
ний с учетом комплекса условий. Такое представление процесса технологического проектирования указывает путь для формализации самого процесса принятия решений. Для этого достаточно описать каким-либо образом весь набор типовых решений, а также условий, при которых может быть применено каждое из них. Тогда процесс выбора сведется к проверке соответствия исходных данных условиям применимости типовых решений; при выполнении всех условий комплекса принимают соответствующее типовое решение.
Совокупность параметров, регламентированных комплексом условий применимости, будем называть комплексом параметров применимости; в данном случае КПП = {D, L, m, a}.
Комплекс параметров применимости является главным определяющим объектом при алгоритмизации задачи нерасчетного характера. Именно он определяет полноту учета всех влияющих факторов, в соответствии с ним формируются исходные данные задачи, характеристики типовых решений.
Далее для решения задачи нужно выявить допустимые для каждого типового решения диапазоны параметров применимости. Соответствующие характеристики зубошевинговальных станков приведены в таблице 4.
В соответствии с комплексом условий применимости для заданного набора исходных данных (параметров детали) из трех имеющихся принимается то решение, которое удовлетворяет неравенствам КУП.
Процедуру проверки этих условий можно описать с помощью алгоритма (рис. 8). На основе этого алгоритма может быть составлена программа, позволяющая для любого набора исходных данных выбрать соответствующее типовое решение (модель станка для зубошевинговальной операции). В этом алгоритме заложен принцип предпочтительности применения станков малых размеров. Например, набору исходных данных {300; 80; 1,75; 35} соответствует решение 1 (станок 5А702Г); набору исходных данных {320; 150; 3; 10} решение 3 (станок 5717С).
Рассмотренный комплекс условий применимости имеет простейшую структуру — совокупность независимых неравенств. Условия применимости могут быть описаны любыми соотношениями параметров (не только неравенствами), а сами параметры применимости могут оказаться взаимозависимыми. В этом случае условия применимости будут иметь более сложный вид.
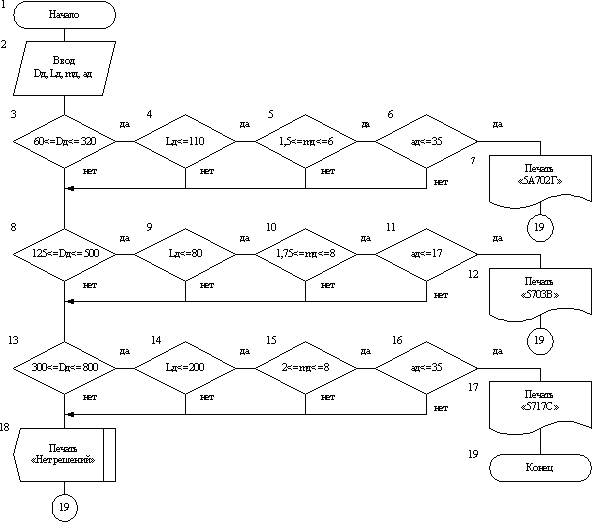
Рисунок 8 – Алгоритм выбора модели станка