5.Вычислить индексы парной корреляции для каждого уравнения.

1.Индекс парной корреляции для уравнения парной регрессии:

2. Индекс парной корреляции для уравнения квадратичной параболы:

=0,0002+0,7160*x+6,6709*

Заменим на .

=

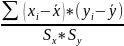
= =0,0033

Вывод: Так как значение индекса корреляции находятся в пределах: отсюда следует, что связь рассматриваемых признаков слабая.

6.Проверить значимость уравнения регрессии:

Оценка статистической значимости уравнения регрессии в целом осуществляется с помощью F-критерия Фишера.

F-критерий Фишера заключается в проверке гипотезы о статистиче-

ской незначимости уравнения регрессии. Для этого выполняется сравнение

фактического и критического (табличного) 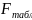значений F-критерия

Фишера.

1. Выдвигаем нулевую гипотезу H₀ о статистической незначимости уравнения регрессии.

2. Рассчитываем фактическое значение F-критерия:

n- число единиц совокупности

m-число параметров при переменных(для линейной регрессии m = 1)

=0,9989

3. Фактическое значение сравниваем с критическим табличным:

F_факт= 0,9989

F_крит= 3,8 при α = 0,05

Вывод:F_факт<F_крит, поэтому Н₀ не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.

4. Для параболического уравнения регрессии F_факт = 3,739

F_крит = 4,067, при α = 0,05.

Вывод:F_факт < F_крит , гипотеза Но принимается, параболическое уравнение регрессии - не значимо.

7. Проверить значимость коэффициентов линейного уравнения.

Для оценки статистической значимости уравнения применяется t-критерий Стьюдента.

1. Выдвигаем нулевую гипотезу H₀ о о случайной природе показателей, т. е. о незначимом их отличии от нуля.

2. Рассчитываем фактическое значение t-критерия для оцениваемых коэффициентов линейного уравнения путем сопоставления их значений с величиной стандартной ошибки.

=

=

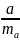
3. Стандартные ошибки параметров линейной регрессии определяются по формулам:

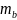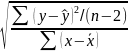= =0,3582

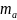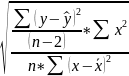= =19,8910

b=2,1194

a=-77,74

4. Сравнивая фактическое и критическое (табличное) значения t-статистики

t_крит и t_факт принимают или отвергают гипотезу Н_о.

=5,9168

= -3,9083

t_крит =1,684 (при уровне значимости 0,05)

 , поэтому Н₀ принимается, т.е. параметр a уравнения линейной регрессии статистически незначим.

 , поэтому Н₀ отклоняется, т.е. параметр b уравнения линейной регрессии статистически значим.

Вывод: Коэффициент регрессии b не случайно отличается от нуля и сформировался под влиянием систематически действующего фактора x. Природа формирования коэффициента регрессии a случайна.

8.Определить лучшее уравнение регрессии на основе средней ошибки аппроксимации.

Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:

1. Вычислим среднюю ошибку аппроксимации для линейного уравнения:

0,9%

2. Вычислим среднюю ошибку аппроксимации для параболического уравнения:

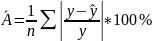=119%

Вывод: Так как построенное уравнение регрессии считается удовлетворительным, если значение A не превышает 10–12 %, то линейное уравнение считается удовлетворительным, а параболическое уравнение признаётся неудовлетворительным. Уравнение линейной регрессии лучшее уравнение, так как у него наименьшая ошибка аппроксимации.