Федеральное государственное автономное

образовательное учреждение

высшего профессионального образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Институт управления бизнес-процессами и экономики

Кафедра «Экономика и организация предприятий энергетического и транспортного комплексов»

Лабораторная работа №1,2 по теме:

Уравнение линейной регрессии

Руководитель ___________________________________________Середа В.А.

Студент УБ 11-02 ____________________________________ Варганова О.И.

Красноярск 2013

Задание:

1. Вычислить линейный коэффициент парной корреляции.

2. Проверить значимость коэффициента парной корреляции.

3. Построить доверительный интервал для линейного коэффициента пар-

ной корреляции.

4. Построить уравнение парной регрессии и квадратичной параболы.

5. Вычислить индексы парной корреляции для каждого уравнения.

6. Проверить значимость уравнений регрессии (линейное и параболическое).

7. Проверить значимость коэффициента линейного уравнения.

8. Определить лучшее уравнение регрессии на основе средней ошибки ап-

проксимации.

9. Построить интервальный прогноз для значения x = «Республика Коми» для линейного уравнения.

10. Определить средний коэффициент эластичности.

Области и республики	Видеомагнитофоны, видеокамеры (y)	Магнитофоны, плееры (x)
1. Белгородская область	39	65
2. Брянская область	37	47
3. Владимирская область	36	61
4. Воронежская область	36	44
5. Ивановская область	26	47
6. Калужская область	43	61
7. Костромская область	31	45
8. Курская область	40	47
9. Липецкая область	48	58
10. Московская область	64	57
11. Орловская область	39	69
12. Рязанская область	34	46
13. Смоленская область	39	55
14. Тамбовская область	37	59
15. Тверская область	35	52
16. Тульская область	54	58
17. Ярославская область	36	47
18. Республика Карелия	49	65
19. Республика Коми	58	59
20. Архангельская область	35	58
21. Вологодская область	34	51
22. Калининградская область	48	53
23. Ленинградская область	30	65
24. Мурманская область	59	63
25. Новгородская область	26	63
26. Псковская область	26	44
27. Краснодарский край	44	60
28. Ставропольский край	40	63
29. Астраханская область	54	55
30. Волгоградская область	41	55
31. Ростовская область	43	57
32. Республика Башкортостан	40	52
33. Республика Марий Эл	28	64
34. Республика Мордовия	33	52
35. Республика Татарстан	52	61
36. Удмуртская республика	32	53
37. Чувашская республика	31	60
38. Кировская область	27	60
39. Нижегородская область	52	36
40. Оренбургская область	47	57
41. Пензенская область	36	47
42. Пермская область	40	50
43. Самарская область	62	56
44. Саратовская область	38	51
45. Ульяновская область	37	51

1. На основании таблицы вычислить линейный коэффициент парной корреляции.

= =0,1488

Вывод: Так как линейный коэффициент парной корреляции =0,1488,

отсюда следует, что между признаками X и Y наблюдается слабая прямая линейная зависимость.

2. Проверить значимость коэффициента парной регрессии.

Для оценки статистической значимости линейного коэффициента парной корреляции применяется t-критерий Стьюдента. Согласно t-критерию выдвигается гипотеза о случайной природе показателей, т. е. о незначимом их отличии от нуля. Далее рассчитываются фактические значения критерия для оцениваемого коэффициента корреляции путем сопоставления их значений с величиной стандартной ошибки:

=

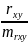
_{Стандартная ошибка коэффициента корреляции определяются по формуле:}

1. =

= =0,1526

2. = =0,9751

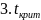(0,05;42)=2,0180

Вывод: Фактическое значение сравниваем с табличным критическим значением:

t_набл  t_крит , то не отклоняется, то есть признаётся случайная природа формирования . Коэффициент признаётся незначимым.

3. Построить доверительный интервал для линейного коэффициента парной корреляции.

Доверительные интервалы определяют пределы, в которых лежат точные значения определяемых показателей с заданной степенью уверенности, со-

ответствующей заданному уровню значимости α.

Для расчета доверительного интервала для линейного коэффициента парной корреляции определяем предельную ошибку ∆

= *

=0,9751*0,1526=0,1487

2. Рассчитаем доверительный интервал

= -

= +

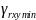= 0,0001

= 0, 2976

Вывод: С вероятностью 0,95 линейный коэффициент парной корреляции находится в пределах от 0,0001 до 0,2976.

4.Построить уравнение парной регрессии и квадратичной параболы.

1. Построить уравнение парной регрессии:

a=Yср-b*Xср

b=

b= =2,1194

a=39,59-2,1194*55,36=-77,7400

2. = a + b⋅x

=-77,74+2,1194*x

_{3. Построим уравнение параболической регрессии:}

= + *x+ *

Парабола второго порядка имеет 3 параметра , , , которые

определяются из системы трех уравнений

+ * + * =

+ + * =

* + * + * = *y

4 5 2479 6145441 1816

6145441 138801 7887157 100509

138801 7887157 454224909 5650363

1	55,08889	136565,3556		40,3556
6145441	138801	7887157		100509
138801	7887157	454224909		5650363

1	55.0889	136565,3556		40,35556
0	1	2479,9935		0,7326

0 240764,1333 -18501183007,467 48971,5334

1	55,0889	136565,3556		40,3556
0	1	0		0,7160
0	0	1		6,6709

1	0	0		0,0002
0	1	0		0,7160
0	0	1		6,6709

=0,0002

=0,7160

=6,6709

=0,0002+0,7160*x+6,6709*