3. Электромагнитные волны в тонких слоях

В настоящее время в научных целях широко используются материалы с управляемым коэффициентом отражения. Большой интерес из них представляют собой тонкие (по сравнению с длинами волн внутри исследуемых образцов) высокопроводящие структуры [1-5, 12, 13, 17-28, 30, 32, 38, 50, 52, 53, 55, 60]. Наиболее последовательный прямой метод расчета состоит в независимом решении волновых уравнений в каждой среде по отдельности с последующим сшиванием полученных решений на границах раздела сред [26, 27]. Однако ввиду крайней громоздкости подобных вычислений (особенно для многослойных структур) были разработаны и более простые методы. Анализ отражения электромагнитных волн, необходимый при выборе или создании поверхности, может проводиться, например, на основе нахождения импеданса, отражающего электромагнитные свойства среды [11, 43], а также другими классическими методами [33, 38, 45].

К значительно более простым вычислениям по сравнению с классическими методами ведет метод усреднения, впервые примененный для расчета волновода с ферритовым заполнением [40], где зависимость поля волны от координаты нормальной слою предполагается линейной. В дальнейшем этот метод получил широкое развитие для различных слоев [6, 26, 27, 59], а в обзоре [59] был дан подробный анализ применимости метода усреднения к различным ситуациям и сравнение его с точным решением.

В данной главе, используя метод усреднения, получены граничные условия для тонкого металлического слоя в свободном пространстве и лежащего на диэлектрической подложке, а также описано поведение коэффициента отражения на основе полученных граничных условий в зависимости от толщины слоя, угла падения волны, частоты электромагнитного излучения, толщины диэлектрической подложки [1, 2, 12, 13, 20-27].

1.4.1. Граничные условия Метод усреднения. Обобщенные импедансные граничные условия для тонкого проводящего слоя

Рассмотрим плоский проводящий изотропный слой, толщиной d, характеризующийся материальными параметрами магнитной проницаемостью и удельной проводимостью (рис. 1.2).

Рис. 1.2. Структура поля вблизи металлического слоя, толщиной d.

Уравнения Максвелла в этом случае имеют вид:

(1.56)

Интегрируя уравнения по толщине слоя, получаем систему усредненных выражений:

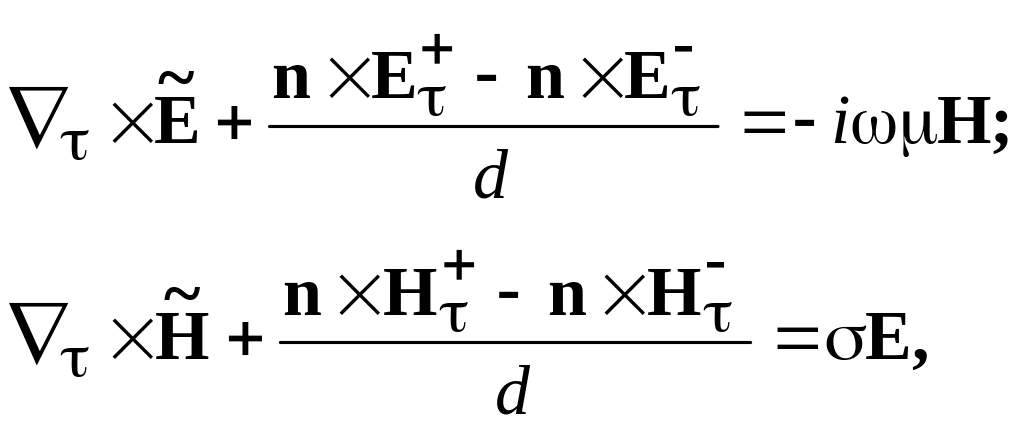(1.57)

г де – двумерный оператор дифференцирования, , – усредненные по толщине компоненты электрического и магнитного полей, – касательные составляющие полей у поверхности слоя при _, – тангенциальные компоненты полей при . Обозначим волновой вектор через , где – поперечная компонента волнового вектора, а – продольное волновое число, – волновое число. Вектор используется в качестве переменной преобразования Фурье, определяемого следующей формулой: . Используя решения уравнения Гельмгольца [6, 59], можно получить соотношения, связывающие усредненные касательные составляющие электрического и магнитного полей с касательными компонентами полей на верхней и нижней границах поверхности:

_(1.58)

где – некоторая функция, связывающая усредненные компоненты полей с полями на границе слоя. Исключая нормальные составляющие полей к поверхности [6, 59], из системы уравнений (1.57), получаем точные соотношения в диадной форме:

; (1.59)

,(1.60)

где – двумерная единичная диада, а – единичные вектора. Уравнения (1.59) и (1.60) могут быть использованы для описания полей вблизи слоев с произвольными толщинами и являются строгими соотношениями для Фурье образов, не содержащие каких-либо приближений. Основной проблемой вывода граничных условий для полей-оригиналов является то, что коэффициенты (1.59) и (1.60) не являются рациональными функциями. Поэтому приходится применять различные приближенные подходы, которые, в сущности, сводятся к аппроксимации функции рациональными функциями .

Рассмотрим частный случай, когда (это имеет место в средах с большими значениями материальных параметров). В этом случае можно установить точный вид функции . Берем решение волнового уравнения Гельмгольца в виде . В нем неизвестные векторные коэффициенты могут быть определены, через поля на верхней границе слоя и – на нижней. Тогда составляющие, например, для электрического поля на границах слоя, будут иметь вид:

(1.61)

Функция связывает усредненные компоненты полей с полями на границах слоя

(1.62)

Решая уравнение

, (1.63)

получаем явный вид функции :

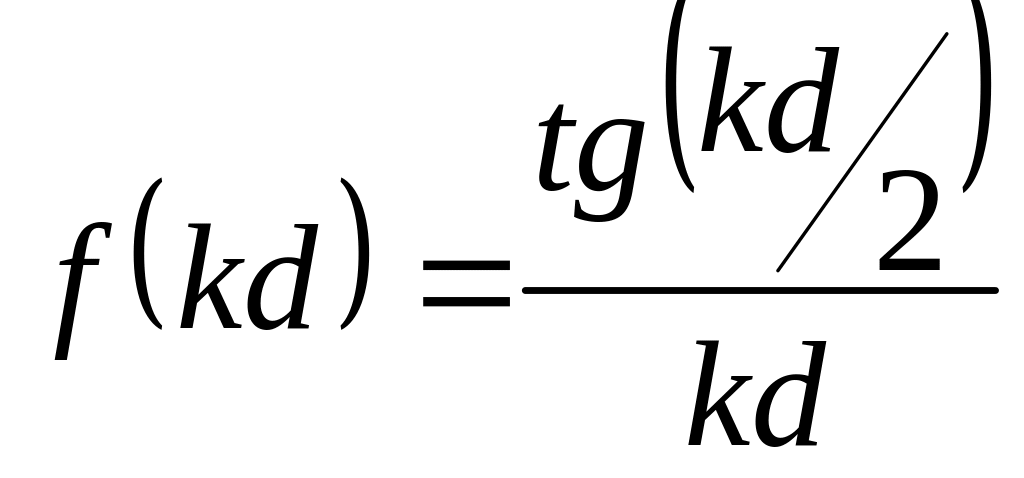. (1.64)

Точные граничные условия для этого случая запишутся в виде [12-14]:

(1.65)

(1.66)