3. А. В. Шпиленко // Экономико-математические модели управления персоналом на предприятии - 49-52 с.

Критерии оптимизации управления персоналом наука об управлении персоналом и методы математического программирования для решения задач управления трудовыми ресурсами до сих пор не получили в нашей стране должного развития и применения однако в последнее время государственные и коммерческие структуры проявляют растущий интерес к научным методам управления персоналом. при решении задач подобного рода приходится учитывать множество различных по степени важности факторов, существование которых обусловлено взаимными требованиями, предъявляемыми друг к другу коллективом, от дельными индивидуумами и организацией. одной из основных проблем науки о руководстве является за- дача распределения трудовых ресурсов, которая включает в себя отбор, расстановку кадров и назначение на должности. обычно отбор на работу в организации осуществляют исходя из текущих потребностей, хотя в некоторых случаях делаются попытки оценить «потенциал» будущего сотрудника с точки зрения его про движения по службе. иногда возникает необходимость найти компромиссное решение между отбором людей с наибольшей производительностью труда на данный момент и кандидатов с наивысшими возможностями в будущем. Основной задачей распределения трудовых ресурсов является расстановка кадров (назначение на должности), обеспечивающая выполнение требуемых видов работ. Задачи распре деления являются «зеркальным отображением» задач использования. если в задачах распределения ресурсов структура работ считается заданной и требуется назначить их исполнителей, то в задачах использования ресурсов заданными являются исполнители, их возможности и индивидуальные характеристики и требуется определить структуру работ, которая позволила бы нм лучшим образом использовать эти возможности. в большинстве случаев при управлении трудовыми ресурсами решаются одно временно обе задачи.

Задача распределения трудовых ресурсов решается в организации на двух уровнях управления. На верхнем уровне решается задача агрегированного планирования трудовых ресурсов, целью которой является определение численности групп сотрудников, необходимых каждой организации; часто эта численность выражается через потребность в человеко-часах и затратах на рабочую силу. Второй уровень – это непосредственное управление. Здесь

результатом является фактическое назначение каждого конкретного исполнителя на конкретную работу, т. е. решение задачи, которая иногда называется задачей оптимального назначения и дает ответ на вопрос, как наиболее эффективно назначить n исполнителей на m работ. Математическая модель задачи о назначениях в общем виде имеет следующую формулировку: найти оптимум целевой функции F({x(i,j)}) при следующих ограничениях:

n

∑ x(i,j) ≤ 1, j = 1,m; (33)

i = 1

m

∑ x(i,j) ≤ 1, i = 1,n, (34)

j = 1

n m

∑ ∑ x(i,j) = min (n,m); (35)

i = 1 j = 1

x(i,j) = 0, 1; i = 1,n, j = 1,m, (36)

где х(i,j) = 0, если работа под номером j не выполняется работником под номером i, и х(i,j) = 1, если работа выполняется. Данная модель требует, чтобы каждый исполнитель был назначен не более чем на одну работу и, соответственно, на каждую работу должен быть назначен не более чем один исполнитель. для специалиста, использующего эту модель в реальных ситуациях, наиболее трудным моментом является определение соответствующей целевой функции. при этом возможно несколько подходов:

1. Максимизация (минимизация) суммы оценок назначений, иными словами, требование найти максимум (минимум) целевой функции:

n m

∑ ∑ c(i,j) * x(i,j), (37)

i = 1 j = 1

здесь с(i,j) должна непосредственно выражаться через такие важные для организации показатели, как время выполнения работы, издержки производства, объем выпуска в единицу времени и т. д. однако довольно часто осуществить это требование трудно, так как каждое значение c(i,j) есть точечная оценка, при получении которой существенную роль играет распределение ошибок.

2. Максимизация вероятности успешного выполнения каждым исполнителем работы, на которую он назначен, т. е. требование найти максимум целевой функции:

n m

∑ ∑ log( p(i,j) ) * x(i,j) , (38)

i = 1 j = 1

где p(i,j) есть вероятность того, что исполнитель под номером i успешно выполнит работу под номером j (0≤p(i,j)≤1). Оценки вероятности того, что исполнитель с определенными характеристика ми удовлетворительно выполнит каждую из работ, могут быть даны на основе статистических данных. Благодаря свойствам логарифмов целевая функция может быть выражена с помощью приведенной выше формулы. После введения понятия «вероятность успеха» или «неудачи» становится возможным рас смотрение других методов оценки значений с(i,j) и подходов к вы бору целевой функции. Среди специалистов нет единого мнения о предпочтительности той или иной целевой функции. каждая конкретная задача управления требует внимательного обсуждения для выбора адекватной целевой функции.

Модели распределительного типа

Модель о максимальном допустимом назначении. пусть имеется m должностей и кандидатов на эти должности. Для каждой пары кандидат i – должность j известно, может ли данный кандидат занимать данную должность. Задача о максимальном допустимом назначении состоит в том, чтобы назначить как можно больше кандидатов на должность при условии, что каждый кандидат может занять не более одной должности и каждую должность может занимать не более чем один кандидат. введем для обозначения допустимости назначений величины b(i,j). при этом b(i,j) = 0, если кандидат может занимать должность, и b(i,j) = 1 в противном случае. Назначение обозначим x(i,j). при этом x(i,j) = 1, если кандидат i занимает должность j, и x(i,j) = 0 в противном случае. Тогда формальная постановка задачи будет выглядеть так:

n m

∑ ∑ x(i,j) ⇒ max (39)

i = 1 j = 1

n m

∑ ∑ b(i,j) * x(i,j) = 0; (40)

i = 1 j = 1

n

∑ x(i,j) ≤ 1, j = 1,m; (41)

i = 1

m

∑ x(i,j) ≤ 1, i = 1,n; (42)

j = 1

x(i,j) = 0, 1; i = 1,n, j = 1,m. (43)

Індекс і набуває значень лише 1 та n? Що за квадратики йдуть далі? Эту задачу можно описать на языке теории графов, используя понятия двудольного графа. двудольным (бихроматическим) называется граф G(X,U) множество вершин которого X можно разбить на два подмножества X = X1 ∪ X2 так, что выполняются следующие условия: X1 ∩ X2 = ∅; для любого ребра e = (x1, x2)∈U, если x1∈ X1, то x2 ∈ X2, если x1∈ X2, то x2 ∈ X1. иными словами, концы любого ребра принадлежат разным множествам. поставим в соответствие каждому кандидату i вершину xi из множества X1, каждой должности j – вершину xj из множества X2. Обозначим допустимость назначения кандидата i на должность j введением ребра (xi, xj) (заметим, что это ребро соответствует b(i,j) = 0 в формальной постановке (1)). Поиск максимального допустимого назначения сводится к поиску максимального множества ребер, имеющих общие концы. Множество ребер графа, не имеющих общих концов, называется паросочетанием. таким образом, поиск максимального допустимого назначения эквивалентен поиску максимального паросочетания.

4. Нятіна Н.Л. Моделі та інформаційні технології управління трудовими ресурсами регіонально-виробничих і соціально-економічних систем/ автореф. дис. … канд. екон. наук: 05.13.06/ Нятіна Наталья Леонідівна; Херсонський національний технічний університет. – Х., 2011- 6-11 с.

Управління підготовкою трудових ресурсів регіону - це багаторівнева система з 4-мя рівнями ієрархії: рівень регіону, рівень окремих організацій (підприємств), рівень структурних підрозділів організацій і рівень окремих робочих місць.

Модель системи формування трудових ресурсів (рис. 2) включає населення, систему освіти, ринок праці та РВСЕС (економіку регіону).

Виділено основних галузей регіону й основних видів економічної й виробничої діяльності, які повинні бути забезпечені напрямками спеціальностей підготовки. Для досліджуваного регіону , , .

ВРП – валовий регіональний продукт

Рис. 2- Структурна модель системи формування трудових ресурсів.

Завдання балансу попиту та пропозиції на ринку праці в регіоні в   році вимагають рішення наступної системи рівнянь:

, (44)

де  – кортеж випуску фахівців з вищою освітою для k спеціальностей;   – кортеж випуску фахівців із середньою освітою для k-ої спеціальності;   – кортеж випуску фахівців з початковою освітою для k-ої спеціальності; - потреби регіону у році у фахівцях. Співвідношення задають кількість спеціалістів, що готуються у регіоні у і році:

. (45)

Ця задача зводиться до наступної багатокритеріальної задачі оптимізації:

(46)

при обмеженнях:

(47)

Для обчислення потреб регіону у фахівцях з різним рівнем освіти у роботі використовується метод співставлення прогнозних даних з даними на основі статистичних обстежень.

Отримано матрицю коефіцієнтів потреб регіону у фахівцях = (табл. 1). Рядки - – галузі й види діяльності, стовпці – . Коефіцієнт  - процентна частка фахівців спеціальності k.

. (48)

Потреби регіону в році у фахівцях:

; (49)

_{; (50)}

. (51)

, , - кортежі потреби регіону в   році у фахівцях з вищою, середньою і початковою освітою.

Вважаємо, що напрямок розвитку регіону не змінюється, тоді коефіцієнти матриць відповідності , і будуть мало змінюватися з часом, структура промисловості регіону індивідуальна, досить стабільна й базується на традиційних для даного регіону видах промислового виробництва.

Читабельність цієї таблиці???? Її змістове наповнення?

Матриця потреб регіону у фахівцях. Таблиця 1

Галузь Спеціальність	1	2	3	4	5	6	7	8	9	10	11	12	13	Сума рядків
1	0,08	0,07	0,01	0,06	0,02	0,01	0,17	0,03	0,08	0,15	0,05	0,09	0,12	0,94
2	0,02	0,02	0,01	0	0	0	0,02	0,03	0	0,11	0	0,01	0,01	0,23
3	0,02	0,03	0,03	0,03	0,2	0,04	0,05	0,03	0,05	0,2	0,1	0,15	0,11	1,04
4	0,01	0	0	0	0	0,02	0,1	0,09	0,01	0,03	0,05	0,02	0,02	0,35
5	0,01	0	0	0	0,05	0	0,09	0,08	0,04	0,02	0,05	0,02	0,02	0,38
6	0,01	0,01	0	0	0,03	0	0,12	0,01	0	0,03	0,05	0,03	0,01	0,3
7	0,02	0	0	0,02	0	0	0	0,01	0,74	0,01	0	0,13	0,06	0,97
8	0,07	0,1	0,02	0,06	0,4	0,28	0,09	0,07	0,01	0,05	0,4	0,25	0,11	1,91
9	0,01	0	0,02	0,02	0,01	0,01	0,09	0,01	0,01	0,11	0,09	0,05	0,2	0,63
10	0,12	0,01	0,02	0,03	0,02	0,01	0,1	0,12	0,01	0,01	0,01	0,01	0,06	0,53
11	0,04	0,05	0	0	0,02	0,05	0,01	0,13	0	0,05	0	0,1	0,01	0,46
12	0,01	0,05	0,05	0,05	0	0,05	0	0,12	0	0,01	0,01	0	0,01	0,36
13	0,02	0	0,01	0,07	0	0,01	0	0,11	0	0,01	0	0	0,01	0,24
14	0	0,06	0,05	0,04	0	0,01	0	0,12	0	0,01	0	0,01	0,01	0,41
15	0,08	0,06	0,04	0,01	0	0,01	0	0	0	0,01	0	0,01	0,01	0,23
16	0,05	0	0,07	0,1	0	0	0	0	0	0,01	0	0,01	0,01	0,25
17	0,03	0	0	0,01	0	0,01	0	0	0	0,01	0	0,01	0,01	0,07
18	0,1	0,1	0,29	0,18	0	0	0	0	0	0,01	0	0,01	0,01	0,65
19	0,04	0,09	0,19	0	0,02	0,03	0	0	0	0,01	0	0,01	0,01	0,4
20	0,03	0,11	0,02	0	0	0	0,01	0	0	0,01	0,12	0,01	0,01	0,29
21	0,07	0	0,1	0	0	0,01	0,02	0	0	0,05	0	0,01	0,02	0,28
22	0,01	0	0,01	0,02	0	0,02	0	0,01	0	0,01	0,05	0,01	0,05	0,18
23	0,04	0,01	0,02	0,03	0,02	0,01	0,1	0	0,01	0,01	0,01	0,01	0,06	0,29
24	0,03	0,01	0	0,02	0	0	0,01	0,01	0	0,03	0	0,1	0,01	0,13
25	0,03	0,01	0	0	0,14	0,01	0,01	0	0	0,01	0	0,01	0,01	0,23
26	0,03	0,04	0,02	0,16	0,02	0,39	0	0,01	0,04	0,01	0	0,01	0,01	0,74
27	0,01	0,02	0,02	0,09	0,05	0,01	0,01	0,01	0	0,01	0,01	0,01	0,01	0,26

Потреби економіки регіону у фахівцях піддаються впливу демографічного фактору й інерційного характеру розвитку економіки. Вони залежать від передбачуваної оцінки значень кортежу зайнятих в економіці в   році. Коефіцієнт ротації  визначає частину, що оновлюється та вливається в економіку в  рік:

(52)

де  , , – кортежі зайнятих в економіці осіб відповідно з вищою, середньою і початковою освітою у   році; , ,  – відповідні значення коефіцієнтів ротації.

Прогноз потреби в кадрах :

(53)

де - потреба регіону в кадрах, викликана збільшенням кількості робочих місць;

- потреба регіону в кадрах, пов'язаних з вибуттям зайнятого населення.

₍₅₄₎

де - частка померлих жителів регіону; - частка тих, що виїхали; - прогнозована кількість зайнятих в економіці; - прогнозована кількість жителів, що досягли пенсійного віку; - частка жителів регіону, що досягли пенсійного віку й припинили працювати.

Використовувалися моделі лінійного тренду, статистичні дані по регіону. Прогноз будувався на використанні даних про природний рух населення.

показує щорічне незначне збільшення потреби, пов'язане з повільним відновленням економіки регіону після кризи за умови збереження тендерів соціально-економічного розвитку регіону на час побудови прогнозу.

Виконано аналіз співставлення системи вищої освіти регіону потребам регіону в кадровому потенціалі. Існуюча система здатна випускати фахівців на замовлення регіону.

5. Набока Р.М. Управління трудовим потенціалом на підприємствах легкої промисловості: автореф. дис. ... канд. екон. наук : 08.00.04 / Набока Руслан Миколайович ; Київ. нац. ун-т технологій та дизайну. - К., 2010. - 20 с.

Управління рухом кадрового потенціалу на підприємстві - це підготовка кадрів для підприємства, прогнозування потреби в кадрах, розподіл складу працівників по видах робіт, планування кар'єри окремих працівників, оцінка праці працівників, оцінка складності праці, загальна оцінка результатів праці.

Алгоритм підбору кадрового складу визначає сукупність елементарних перевірок, послідовність їхньої реалізації й правила обробки результатів, реалізованих елементарних перевірок з метою одержання оцінки результатів підбора кадрового складу.

Результати елементарної перевірки можуть бути використані як ознаки розбиття множини Е на класи. Використовуючи таке трактування елементарних перевірок і їхніх результатів, алгоритм підбору професійних параметрів кадрового складу можна представити орієнтованим графом, деревом. Реалізація будь-якої елементарної перевірки вимагає певних витрат часу, ресурсів. Витрати є ціною елементарної перевірки - , або , .

Кожному професійному стану , об'єкту підбору професійних параметрів кадрового складу приписані деяке додатне число або , - вага професійних навичок — стану , стану серед інших станів множини Е. Вагою професійних навичок може бути ймовірність, з якої об'єкт підбору професійних параметрів може перебувати в цьому професійному якості-стану. При цьому й .

Як характеристика якості алгоритму прийняті середньозважені витрати на виділення одного стану об'єкта

. (55)

Побудова оптимального алгоритму підбору професійних параметрів кадрового складу складається з вибору множини елементарних перевірок і послідовностей їхньої реалізації, які забезпечують мінімум цільової функції (1).

Планування кар'єри працівника – організація його просування по щаблях посадового й кваліфікаційного росту. Найбільш близькими до управління кар'єрою є «завдання про призначення». Варіант цього завдання полягає в розміщенні персоналу – призначенні співробітників на посади, щоб максимізувати сумарний ефект від діяльності співробітників. Використовуються ланцюги Маркова.

Кінцевий дискретний ланцюг визначається:

– множиною станів ;

– кортежем початкових імовірностей , що визначає ймовірності того, що в початковий момент часу процес перебував у стані ;

– матрицею перехідних імовірністей , що характеризує ймовірність переходу процесу з поточного стану в наступне .

Розглянуто марковський ланцюг, вершини якого відповідають рівням ієрархії посад і належать упорядкованій множині, .

Додання в вершину свідчить про звільнення робітника з організації. При цьому - імовірність того, що робітник залишився на тому ж рівні; - імовірність, що він переходить на j-й рівень, ; - імовірність, що робітник звільнюється; імовірності дорівнюють «0» (пониження по роботі неможливе).

Марковський ланцюг, який описує кар’єру робітника буде мати вигляд (рис. 1):

Рис. 1 - Марковський ланцюг, що описує кар’єру робітника.

Завдання по створенню пропозицій індивідуальної кар’єри робітників організації може бути виміряне за допомогою марковських ланцюгів.

Завдання управління кар'єрою розглядається як завдання узгодження інтересів співробітника й організації.

Завдання розміщення працівників по видах робіт: є співробітників , яких необхідно розподілити по видах робіт .

Нехай продуктивність -го співробітника по роботі, - призначення -го співробітника на -ую роботу приймає значення:

, якщо співробітник призначений на роботу ; , не призначений.

Критерій оптимуму – сумарна продуктивність співробітників. Цільова функція: .

6. Ющенко Н.Л. Моделювання системи професійно-кадрового забезпечення малого бізнесу на регіональному рівні: автореф. дис. канд. екон. наук : 08.03.02/ Ющенко Надія Леонідівна; Київський національний економічний університет. – К., 2001. – 9-13 с.

Ці моделі Ви вже взяли з монографії інавели у каталозі під №1!!!

На підґрунті соціально–економічної теорії гнучкого ринку праці та системного підходу в дисертації запропонована концепція раціонального функціонування ринку праці на регіональному рівні. Цим самим нами пропонується власний підхід до побудови економіко–математичних моделей системи професійно–кадрового забезпечення підприємств з урахуванням фактора невизначеності в умовах існування неповного інформаційного забезпечення; оптимізації процесу підготовки, перепідготовки і підвищення кваліфікації, розподілу працівників та їх ефективного використання з метою отримання раціонального обсягу витрат.

На базі запропонованої концепції сформована двохетапна стохастична динамічна модель.

Нехай в інтервалі часу [1, Т] потрібно m осіб, що стоять на обліку в обласному центрі зайнятості, влаштувати на роботу, а підприємствами подано інформацію про наявність n вакантних місць. Інтервал [1, T] розіб’ємо на ряд підінтервалів (t=1,…,T), на кожному з яких слід визначити кількість осіб, що призначені на відповідні посади, можливо, провівши попередньо підготовку, перепідготовку чи підвищення кваліфікації безробітних громадян. Необхідність такого підходу щодо регулювання функціонуванням ринку праці певного регіону полягає в наступному:

1. змінюваність у часі попиту на трудові ресурси і періодичність розподілу випускників навчальних закладів;

2. сезонність пропозиції і потреби в окремих категоріях працівників.

Для налагодження регулювання функціонуванням ринку праці в момент часу t=1 необхідно знати кількість громадян, які завершили навчання і потребують подальшого працевлаштування в залежності від потреб підприємств регіону. Необхідно визначити також, кого з безробітних осіб, що стоять на обліку в службі зайнятості, направити на професійне навчання, перепідготовку та на підвищення кваліфікації, як забезпечити їх працевлаштування в кожен момент часу t=1,…,T, так, щоб сумарні витрати, пов’язані з підготовкою і використанням, були б найменшими. При цьому регулювання здійснюється в два етапи:

1. визначаються обсяги направлень на навчання осіб, з тих, котрі потребують набуття або поліпшення своїх професійних якостей у відповідності з вимогами гнучкого ринку праці, до того моменту часу, як стає відомим попит на кадри відповідної кваліфікації;

2. визначається обсяг призначень (проводиться направлення) осіб на роботу після того, як стане відомою заявка кожного з роботодавців.

Величина попиту на трудові ресурси з боку підприємств є випадковою на момент прийняття початкового рішення. Її значення стають відомими на момент часу t.

Введемо позначення: i – індекс базового рівня підготовки безробітних громадян (i=1,…,m); k – індекс напрямків підготовки громадян в закладах освіти (k=1,…,p); j – індекс вакансій (j=1,…,n); a – гранична кількість осіб, які стоять на обліку в регіональному центрі зайнятості; r_k – гранична кількість місць в закладах освіти за k–тим напрямком підготовки; x_k – обсяг випуску за k–тим напрямком в початковий момент часу (t=1); y_k(t) – кількість спеціалістів з k–тою освітою в момент часу t, t=1,…,T, тобто до моменту призначень на вакантні робочі місця, заплановані на t–й період; w_j(t) – величина попиту на j–у вакансію (j–го фахівця) на момент часу t (на час прийняття рішення про направлення на роботу), ця величина вважається випадковою, адже поки проводиться підготовка кадрів попит може змінюватися; d_j(t) – дефіцит на j–х спеціалістів в момент часу t; v_kj(t) – обсяг направлень осіб з k–ю підготовкою на j–те робоче місце в момент часу t; r_ij(t) – гранична пропускна здатність закладів освіти, що здійснюють приведення у відповідність і–го базового рівня підготовки осіб, які стоять на обліку в службі зайнятості, щодо вимог роботодавців стосовно кожного претендента на j–у вакансію; l_k – витрати на підготовку одного безробітного за k–м напрямком; – витрати на перепідготовку однієї особи за k–м напрямком протягом періоду часу t; – питомі втрати підприємств, пов’язані з наявністю j–ої вакансії в підінтервалі t; c_kj(t) – витрати, пов’язані з ефективним використанням працівника з k–м рівнем підготовки на j–ому робочому місці протягом підінтервалу t.

Таким чином, використовуючи введені позначення, отримуємо наступну динамічну двохетапну модель управління (регулювання) формуванням кадрового потенціалу, що складається з двох взаємопов’язаних задач.

Задача першого етапу: необхідно знайти такий початковий стан ринку праці – початкові обсяги підготовки за k–м напрямком x_k, для яких

(56)

з урахуванням обмежень

(57)

(58)

Тут Mg(x, w) – математичне сподівання функції g(x, w), яка для кожного x є випадковою величиною.

Задача другого етапу: визначити обсяги призначень (направлень) осіб на роботу при фіксованих обсягах випусків x=(x₁,…,x_k) і відомому попиті w= =(w₁(1),…,w₁(T),…,w_n(1),…,w_n(T)) так, щоб

(59)

Множина W(x,w) задається співвідношеннями:

(60)

(61)

(62)

(63)

(64)

Задача (57)–(64) є двохетапною, в ній чітко виділені два етапи прийняття рішення: перший (57)–(59) – прийняття рішення про початкові обсяги підготовки, другий (60)–(64) – розподіл підготованих фахівців по підприємствах після того, як стане відомою величина попиту.

У дисертації ця економіко–математична модель редукована також до відповідної лінійної задачі (на підґрунті відповідної системи гіпотез) з метою спрощення.

Нехай m осіб необхідно призначити на n посад.

Пропозиція робочої сили формується за рахунок таких джерел:

• вивільнені з народного господарства в зв`язку з ліквідацією, реорганізацією та перепрофілюванням підприємств, установ, організацій, скороченням чисельності працівників;

• звільнені за власним бажанням та за порушення трудової дисципліни;

• випускники навчальних закладів, які потребують працевлаштування;

• раніше зайняті в домашньому господарстві та інші категорії незайнятого населення.

Разом з тим маємо такі два основні потоки:

1) особи, які вивільняються з підприємств, організацій, установ ( для цього потоку характерна наявність певного стажу роботи, оволодіння принаймні однією професією, отриманою в навчальному закладі або на виробництві, гостра потреба працевлаштування на нове робоче місце );

2) особи, які раніше не працювали або давно залишили роботу, не мають професії або втратили професійні навички.

У представників цих двох потоків по різному проявляється ставлення до вибору профілю, місця і терміну навчання, інших чинників, які потребують диференційованого підходу. Це враховується при розподілі пріоритетів.

Надходження на місця відбувається через систему підготовки і перепідготовки кадрів ( через проміжні пункти ), тобто існує певна кількість закладів по підготовці і перепідготовці кадрів з набором в p місць в межах регіону.

Попит, пропозиція робочої сили і обсяг набору в заклади по підготовці і перепідготовці кадрів (m, n, p) є варіюючими параметрами. У межах загального заповнення вакансій в навчальних закладах і на кожну з посад особи поступають у відповідності з призначеними для них пріоритетами (кількісними та якісними).

Відомі витрати C_ik на отримання i–тою особою k–го освітньо–кваліфікаційного рівня та спеціальності і C_kj – ефективність використання відповідного виконавця на відповідному робочому місці з множини робіт. Нехай для визначеності C_kj  – витрати на виконання виконавцем з k–м рівнем підготовки j–ї роботи.

В якості критерію оптимальності виступає мінімізація сумарних витрат.

Щоб сформулювати задачу математично, вводимо функції f_ik і f_kj, які відображають факт призначення у відповідності зі змінними пріоритетами. Вони приймають значення 1 або 0. Нехай x_i ( ) – набір кількісних і якісних характеристик i–го незайнятого громадянина (стать, вік, рівень освіти, спеціальність, досвід роботи, особисті риси і т. ін.); z_k ( ) – набір характеристик k–го вільного місця в закладах освіти (напрямок підготовки, спеціальність, освітньо–кваліфікаційний рівень); y_k ( ) – набір характеристик випускників закладів освіти з k–ою кваліфікацією; s_j ( ) – набір вимог роботодавців щодо кандидатів на заповнення j–го вільного робочого місця. Тоді

Таким чином, математична модель задачі набуває наступного вигляду:

F=

; (65)

  ; (66)

  ; (67)

, (68)

де f_ik, f_kj – булеві змінні (f_ik  {0;1}, f_kj {0;1}).

Обмеження (65) вказує на те, що кожне місце в закладах по підготовці і перепідготовці кадрів може бути зайняте лише однією особою, (66) – кожна особа може займати лише одне місце в закладах підготовки і перепідготовки кадрів, (67) – на кожну посаду може бути призначена лише одна особа, (68) – кожна особа повинна бути призначена на одну вакантну посаду.

У дисертаційній роботі також сформовано комплекс математичних моделей управління трудовими ресурсами підприємства, до якого, зокрема, ввійшли моделі динамічного програмування, цільового програмування, а також потокові моделі. Це моделі комплектування штату підприємства, розподілу працівників та їх ефективного використання, підвищення кваліфікації.

Побудова комплексу економіко–математичних моделей забезпечує умови для створення і функціонування комп’ютеризованого моніторингу з метою регулювання ринку праці.

7. http://www.bestreferat.ru/referat-131539.html

Планування персоналу є сферою внутрішньофірмового планування, в ході якого оцінюється потреба фірми в персоналі та визначаються заходи по її забезпеченню. Робота з планування персоналу складається з:  1.оцінки наявного персоналу за якісними і кількісними характеристиками;  2.розрахунку поточної і перспективної потреби в персоналі;  3.розробки програми заходів по покриттю потреби в персоналі: найм, навчання, просування і звільнення працівників.  Оцінка наявних ресурсів орієнтована на аналіз змісту виконуваних у фірмі робіт, що дозволяє визначити кваліфікаційні вимоги до різних професійних груп працівників і ступінь їх відповідності цілям фірми. У результаті такого аналізу визначається укомплектованість фірми працівниками (їх нестача або надлишок) і робиться розрахунок поточної потреби в них або скорочення їх чисельності. Розрахунок перспективної потреби в персоналі є більш складним завданням, тому що носить прогнозний характер і орієнтований на можливі зміни діяльності фірми. У ході цієї роботи аналізуються показники та причини можливого відтоку персоналу (відомості про види і причини звільнення). Ця робота базується на моделях прогнозу потреби в персоналі, найбільш поширеними з яких є економетричний метод.  Останній етап планування потреби в персоналі передбачає розробку програми заходів по найму, підготовки, просування і звільнення працівників, виходячи з розрахованої на попередніх етапах планування потреби в них.  У запропонованій моделі планування трудових ресурсів повинні бути розраховані всі витрати, пов'язані: з вартістю утримання працівника  відповідної посади; з наймом нового працівника на відповідну посаду;  зі звільненням працівника. Витрати на працівника включають всі виплати, пов'язані з використанням праці, і складаються з наступних елементів:  Для оцінки матриці переходів Маркова, використовуваної в моделі планування трудових ресурсів, слід оцінити ймовірності переходу працівників з однієї службової категорії в іншу. Для цього можуть бути використані дані з планування кар'єри кожного працівника фірми.  Планування кар'єри працівника являє собою організацію його просування по щаблях посадового й кваліфікаційного росту, що допомагає йому розвинути і реалізувати професійні знання і навички в інтересах фірми.  У діяльності служби управління персоналом з планування кар'єри працівників відбувається найбільш гармонічне поєднання інтересів і цілей фірми (гарантування вкладень у підготовку працівників, забезпечення їх лояльності інтересам фірми, зменшення плинності, ефективне використання) з індивідуальними інтересами і цілями самих працівників (задоволення потреб у самоповазі та визнання , в досягненні незалежності). Це дозволяє сформувати продуктивні і стійкі відносини між ними. Тому робота з планування кар'єри будується на індивідуальному підході до можливостей професійного просування і росту. Управління кар'єрою працівників певною мірою є природним продовженням і результатом усієї діяльності служби управління персоналом. Даний процес починається вже на етапі найму, в ході якого претенденту повинна бути представлена ​​повна і достовірна інформація про можливості і перспективи роботи у фірмі.  Добре організована робота у всіх сферах управління персоналом, що дозволяє фірмі не тільки забезпечувати себе кваліфікованими працівниками, а й будувати на цій основі цілісну політику підготовки і просування працівників усередині фірми, отримала назву внутрішньофірмового ринку праці.  Створення внутрішньофірмового ринку праці дозволяє фірмі в певній мірі бути незалежною від коливань зовнішнього ринку трудових ресурсів. Однак формувати такий ринок у повному обсязі, як правило, можуть дозволити тільки великі корпорації, що мають можливості орієнтуватися на збереження і розвиток потенціалу кожного співробітника і створюють для цього умови. Основним завданням, яке вирішує організація внутрішньофірмового ринку праці, є збереження накопиченого у фірмі досвіду та кваліфікації, запобігання їх витоку і страхування вкладень у підготовку працівників. Умовою ефективності внутрішньофірмового ринку праці стає безперервне навчання і підвищення кваліфікації працівників, що дозволяють планувати і будувати їх просування у фірмі.  До недоліків внутрішньофірмового ринку праці можна віднести ослаблення конкуренції працівників, тому що при вирішенні питань їх просування основним критерієм є не індивідуальні характеристики, а стаж роботи у фірмі.  Останній вид витрат, який повинен бути оцінений при використанні моделі планування трудових ресурсів, це витрати, пов'язані з вивільненням і звільненням персоналу. Вивільнення персоналу являє собою сферу управлінської діяльності щодо скорочення чисельності працівників. Необхідність скорочення чисельності працівників у фірмі може бути викликана різними обставинами, як внутрішніми, так і зовнішніми.  Пропонована нами двоетапна модель планування трудових ресурсів дозволяє:  1.визначати зміни чисельності персоналу в залежності від вартісних показників;  2.мінімізувати сумарні витрати в аналізований період;  3.враховувати обмеження на витрати забезпечення персоналом протягом всіх періодів планування.  Відомі параметри;  - t   - Аналізовані періоди часу (Т + 1 дискретних в часі крапки); 

- До _i (0) - кількість працівників у початковий період часу для i -Ої службової категорії, i =   ;  - K _i (T) - мінімально необхідна кількість працівників у період часу  t, t   , Для i -ої службової категорії, i =   ;  - B(t) - бюджет періоду t,t   ;  - C _i ¹ (t), C _i ² (t), C _i ³ (t) - витрати на утримання, найм та звільнення співробітника i-ої службової категорії в період t відповідно, t   , I =   ;  - Α _i (t), β _i (t) - штрафні ваги, використовувані для формування критеріїв, t   ,I=   ; 

 M= - Матриця переходів Маркова (будується шляхом обробки експериментальних даних [1]), де m _ij - Ймовірність переходу працівника з категорії i в j заодинперіод, i =   , J =   . Шукані величини: x _i (t)-кількість працівників i -Ої категорії в період t, t   , I =   ;  h _i (T) - кількість працівників, яке необхідно залучити в i -У категорію в період t,t   , I=   ; f _i (T) - кількість працівників i-ої категорії, яких необхідно скоротити в період t, t   , I =   ;  d _i ¯ (t), d _i ⁺ (t) - відхилення від необхідної кількості трудових ресурсів категорії i, i =   , В період t, t   , Вниз і вгору відповідно.  За ідеальних умов хотілося б протягом періоду t для кожної службової категорії мати в точності k _i (T) працівників. Проте залежно від вартісних показників може бути більш вигідним відхилення чисельності працівників як в одну, так і в інший бік від мінімальних потреб. На першому етапі вирішення задачі проводиться визначення чисельності працівників кожної службової категорії методом динамічного програмування, в результаті застосування якого мінімізуються сумарні витрати. Якщо x _i (T) - кількість фактично працюючих i - Ой службової категорії в період t, то можливі витрати трьох видів:  - З _i ¹ (t) (x _i (T) - k _i (T)) - страти, пов'язані з необхідністю утримувати надлишок x _i (T)-k _i (T) працівників i -Ой службової категорії;  - З _i ² (t) (x _i (T) - x _i (T -1)) - витрати, пов'язані з необхідністю додаткового найму x _i (T)-x _i (T-1) працівників i -ої службової категорії;  - З _i ³ (t) (x _i (T -1) - x _i (T)) - витрати, пов'язані з необхідністю звільнення x _i  (T-1)-x _i (T) працівників i –ої службової категорії.  Елементи моделі динамічного програмування визначаються для кожної службової категорії наступним чином: 1) етап t представляється порядковим номером періоду t, t   .  2) варіантами рішення на етапі t є значення x _i (T) - кількість працівників за періоду t.  3) станом (управлінням) на етапі t є x _i (T -1) - кількість працівників протягом періоду t-1.  Рекурентне рівняння динамічного програмування представляється у вигляді: 

(69) де t   ,   .  Обчислення починаються з етапу T при x _i (T) = k _i (T) і закінчуються на етапі t =1.

Оптимальне рішення:

 (70)  У результаті обчислень, проведених методом динамічного програмування будуть знайдені величини x _i (t), h _i(t), f _i (t) для всіх службових категорій i =   в періоді t   , При цьому буде знайдено мінімальне значення сумарнихвитрат. Якщо отримані сумарні витрати все-таки не вкладаються в наявний бюджет підприємства, то на другому етапі вирішення даного завдання визначаються оптимальні відхилення від знайдених кількостей працівників. Зменшення кількості працівників може бути проведене за допомогою наступної моделі, що дозволяє враховувати можливість переходу працівників з однієї службової категорією в іншу і бюджет періоду.  Критерії (зважена сума небажаних відхилень від необхідної кількості працівників): 

  , I =  Обмеження:  1) за кількістю працівників у кожній службової категорії в періоди часу t, t   (У ці обмеження підставляються знайдені на першому етапі величини x _i (T) замістьпотрібних k _i (T))   i=   ;   i=   ;  2) бюджетні

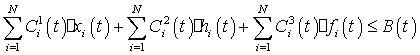 , T   ;  (71)

3)перехідні   , I=   ,T   ;  (72) 4) вимоги неотрицательности всіх змінних моделі та залежності змінних. Змінні небажаних відхилень залежні у тому сенсі, що тільки одна з пари цих змінних може приймати позитивне значення. Те ж саме умова повинна бути виконана, і для змінних h _j (t) і f _i (T), що визначають кількість найманих та звільняються i - ої службової категорії в період t. Дані вимоги визначаються наступними співвідношеннями:   ,     ;  (73)  ,     .  (74) Поставлена ​​задача є задачею багатокритеріальної оптимізації, для розв'язання якої пропонується скористатися розробленим нами інтерактивним методом поступок. Використання методу поступок для вирішення задачі багатокритеріальної оптимізації передбачає, що ОПР повинен на першому етапі вирішення задачі порядок критерії по мірі їх значимості. Значимість кожного критерію в поставленому завданню відповідає важливості забезпечення ресурсами відповідної посади. Потім на кожному наступному етапі вирішується однокритерійним завдання оптимізації у відповідності з наступним алгоритмом.  У загальному випадку математична постановка задачі багатокритеріальної оптимізації з безліччю допустимих рішень   і векторної цільової функцією    може бути записана так: 

Або (75)

    (76) Будемо вирішувати завдання мінімізації векторного критерію. Рішення задачі за методом поступок проводиться у кілька етапів:  1) розташувати критерії   за їх значимістю (найбільш важливий з точки зору ОПР розташовується першим);  2) знайти оптимальне значення     цільової функції   _;  3) зробити поступку за першим показником ефективності, тобто погіршити величину   дозначення   ;  4) запровадити у завдання додаткове обмеження   ;  5) знайти оптимальне значення f ₂ цільової функції   ;  6) зробити поступку по другому показнику ефективності, тобто погіршити величину   дозначення   ;  7) запровадити у завдання додаткове обмеження   ;  8) нове завдання з двома додатковими обмеженнями вирішити по третьому показником ефективності і т.д. Процес рішення задачі закінчується, коли рішення буде отримано за всіма показниками.  Визнаним недоліком відомого методу поступок є складність підбору відповідних поступок, їх вибір потребує дуже ретельного підходу. При завданні занадто малих значень поступок можлива така ситуація, що оптимізація за менш значущим критеріями може бути зовсім не проведена, що не завжди буде влаштовувати ОПР. Для подолання цього недоліку і пропонується інтерактивний метод поступок, який дозволяє в зручному інтерактивному режимі простежити вплив зробленої поступки на вирішення завдання (чутливість рішення задачі до заданої поступку) і підібрати поступки відповідно до власних уподобань ОПР.  Розроблений нами алгоритм інтерактивного методу поступок включає в себе наступні етапи. 1. Формування вихідних даних:  1.визначення кількості критеріїв п і кількості змінних т;  2.визначення функцій критеріїв і обмежень:    2. Ранжування критеріїв у міру їх значущості. Значимість кожного критерію в поставленому завданню відповідає важливості забезпечення персоналом відповідноїпосади.  3. Рішення n завдань однокритерійним умовної оптимізації (без поступок) методом штрафних функцій з кожним заданим критерієм.  4. Демонстрація користувачеві отриманих рішень. Покласти i = 1.  5. Покласти i: = i + l. Надати ОПР вибрати діапазон зміни поступок по (i - 1) - му критерію, задавши значення мінімально можливої ​​поступки min _Δ, максимально можливої ​​поступки max _Δ і кроку зміни поступок h (У% від оптимального значення   -Го критерію).  6. Рішення методом штрафних функцій 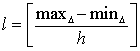  задач умовної оптимізації такого вигляду:     де  7. Демонстрація ОПР графіка зміни рішення i-ої завдання умовної оптимізації в залежності від поступок і значень оптимальних рішень.  8. Вибір ОПР поступки   _, Яку він згоден допустити по (i -1) Критерієм, виходячи з отриманих графіків і особистих переваг.  9. Додавання до наявних обмеженням завдання функціональне обмеження з обраної ОПР поступкою:  10. Якщо i = n, то завершити алгоритм, інакше перейти до п.5.  Якщо ОПР не задовольняє отриманий результат, то йому надається можливість повернутися на будь-який попередній етап побудови рішення.  Після проведення другого етапу будуть скориговані рішення, отримані на першому етапі, при цьому будуть враховані поточні бюджетні можливості підприємства.  Перевагою даної моделі є те, що підзадачі, сформульовані на першому і другому етапах, можуть використовуватися для вирішення відповідних самостійних завдань.