Г) Коефіцієнт покриття характеризує відношення мобільних (оборотних) засобів лікувально-профілактичного закладу до його короткострокової заборгованості. Розраховується за формулою:
,
(22.4)
де
–
коефіцієнт покриття;
– мобільні засоби лікувально-профілактичної установи, грн.;
–розмір короткострокових кредитів, грн. Коефіцієнт покриття показує платіжну можливість лікувально-профілактичної установи, яка оцінюється при умові не тільки своєчасних розрахунків з дебіторами і сприятливої ситуації в реалізації медичних послуг, але й продажу у випадку необхідності інших елементів матеріальних оборотних засобів.
23. Карпишин Н.І. фІНАНСОВЕ ЗАБЕЗПЕЧЕННЯ охорони здоров’я В РЕАЛІЗАЦІЇ ДЕРЖАВНИХ ФУНКЦІЙ НА РИНКУ МЕДИЧНИХ ПОСЛУГ: автореф. дис. на здобуття наук. ступеня канд. економ. наук : спец. 08.04.01 - фінанси, грошовий обіг і кредит / Карпишин Н.І. - Тернопіль, 2008. – 79, [1] c.
Для вирішення проблеми низької оплати праці у державному секторі охорони здоров’я доцільно запровадити гонорарний метод оплати медичних послуг і встановити шкалу гонорарів й удосконалити діючий механізм грошових розрахунків між медичними закладами охорони здоров’я та їх пацієнтами. З метою економного використання фінансових ресурсів запропоновано використовувати принципи аутсорсингу і дозволити медичним закладам делегувати окремі обов’язки, не пов’язані з лікувально-профілактичною діяльністю, іншим фірмам. Це сприятиме зменшенню витрат цих закладів, оскільки таким способом оплачують тільки вартість одержаних послуг, а не утримання працівників та підрозділів, що виконують даний обсяг роботи.
Детально розглянуто проблему вдосконалення порядку бюджетного планування видатків на охорону здоров’я з місцевих бюджетів і розраховано коригуючий екологічний коефіцієнт, який має сприяти справедливішому розподілу коштів між бюджетом Автономної Республіки Крим і обласними бюджетами з урахуванням фактора екологічної ситуації адміністративно-територіальної одиниці. Діючу формулу розрахунку обсягу видатків на охорону здоров’я для бюджету Автономної Республіки Крим та обласних бюджетів запропоновано вдосконалити таким чином:
Vzob(ark) = Hzob(ark) Ni (К ек)і (1 – + Kzi 2) + Vzgi, (23.1)
де (Кек)і – коригуючий екологічний коефіцієнт для бюджету Автономної Республіки Крим і обласних бюджетів.
На покриття потреб охорони здоров’я, спричинених станом екології, запропоновано надавати обсяг бюджетних коштів, який дорівнює добутку загальної кількості населення країни на суму, еквівалентну 20% фінансового нормативу бюджетної забезпеченості на охорону здоров’я для бюджету Автономної Республіки Крим та обласного бюджету. На підставі цього коригуючий екологічний коефіцієнт (Кек)і розраховано за формулою:
(Кек)і = 0,8 + 0,2(К)і, (23.2)
де (К)і – екологічний коефіцієнт для Автономної Республіки Крим і областей.
Основою розрахунку екологічного коефіцієнта є обчислені середньорічні показники рівня екологічного забруднення на 1 тис. населення в Україні, Автономній Республіці Крим і областях за період 1999–2003 рр. за окремими видами ресурсів (повітря, води і землі).
З метою ефективного і раціонального використання бюджетних коштів розроблено економіко-математичну модель оптимізації витрат лікувально-профілактичного закладу на закупівлю медикаментів і виробів медичного призначення:
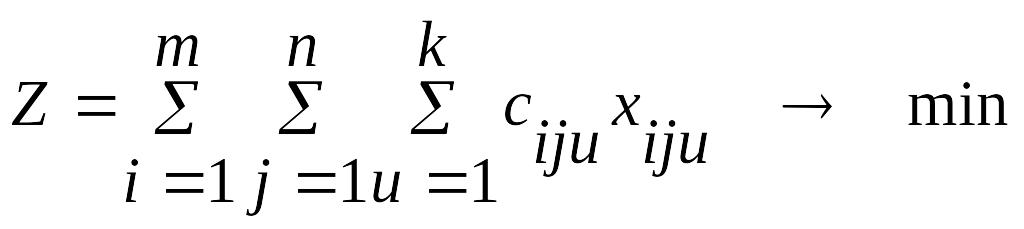(23.3)
за виконання таких умов:
із забезпечення лікарськими засобами в необхідному обсязі:
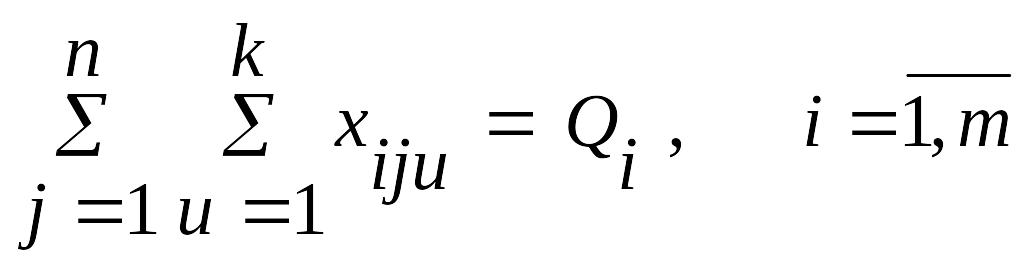
(23.4)
із забезпечення відповідної рейтингової оцінки лікарських засобів:
,
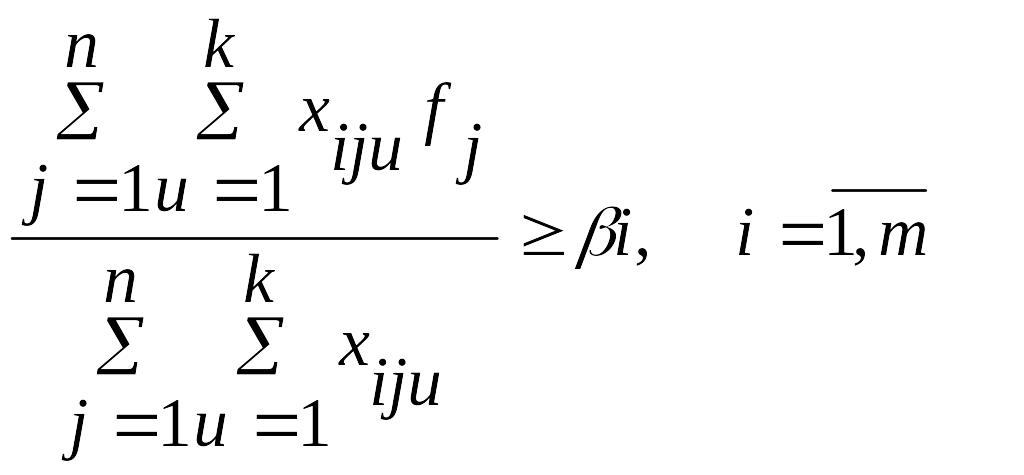(23.5)
де ві – нижня межа рейтингової оцінки лікарських засобів (виробів медичного призначення), яку встановлює менеджер лікувально-профілактичного закладу;
за невід’ємністю та цілісністю змінних:
,
– цілі величини,
(23.6)
де
i
– індекс виду медикаментів (виробів
медичного призначення),
;
j – індекс фірми-виробника фармацевтичної
продукції; u
– індекс фірми-дистриб’ютора,
;
–
ціна i-го
виду медикаментів (виробів медичного
призначення) j-ої
фірми виробника, придбаного в u-го
дистриб’ютора;
–
кількість одиниць i-го
виду медикаментів (виробів медичного
призначення) j-го
виробника, яку лікувально-профілактичний
заклад купить у u-го
дистриб’ютора;
–
рейтингова оцінка j-ої
фірми-виробника;
– планова потреба лікувально-профілактичного
закладу в i-му
виді медикаментів (виробів медичного
призначення).
Представлена модель дає змогу оптимізувати суму грошових коштів на придбання необхідного обсягу медикаментів (виробів медичного призначення) з урахуванням показника рейтингової оцінки фірм-виробників фармацевтичної продукції й усунути суб’єктивні фактори при прийнятті управлінських рішень у системі тендерних відносин.
24. Лонін Є.Б. НАУКОВЕ ОБҐРУНТУВАННЯ ТА РОЗРОБКА МОДЕЛІ ЗАВАНТАЖЕННЯ ЛІКУВАЛЬНИХ ЗАКЛАДІВ ОХОРОНИ ЗДОРОВ’Я ПАЦІЄНТАМИ автореф. дис. на здобуття наук. ступеня канд. мед. наук : спец. 14.03.11 - медична та біологічна інформатика і кібернетика/ Логін Є.Б. - Тернопіль, 2005. – 39, [1] c.
Системні дослідження дозволили визначити, що завантаження лікувальних закладів охорони здоров’я пацієнтами є результатом динамічної взаємодії їх надходження, виписки та послідовного переміщення по місцях надання медичної допомоги та лікування.
Пересування пацієнтів у системі закладів охорони здоров’я (далі СМО – система медичного обслуговування) можна представити у вигляді графа, в якому вузли будуть відповідати місцям знаходження (обслуговування) їх, а “ребра” – пересуванню з одного місця до іншого. Топографія пересування кожного пацієнта буде залежати від особливостей поранення (захворювання або ураження), організаційних факторів тощо. Тому поранені, хворі хірургічного та терапевтичного профілю різного ступеня тяжкості, а також хворі тих чи інших класів, груп, підгруп і нозологічних форм захворювань розділяються на однорідні за медичними та евакуаційно-транспортними характеристиками групи (далі – категорії пацієнтів).
В
результаті СМО може представлятися як
мережа (рис. 24.1), вузлами (
)
якої, в залежності від рівня деталізації,
можуть бути групи відділень (кабінетів)
закладів охорони здоров’я, підрозділи
(відділення або кабінети) закладів або
окремі лікарі (лікарсько-сестринські
бригади), “ребрами” (
,
)
– потоки пацієнтів в дозволеному
напрямку від вузла k
до вузла n
або навпаки:
, (24.
1)
де: 
– кількість
вузлів обслуговування.
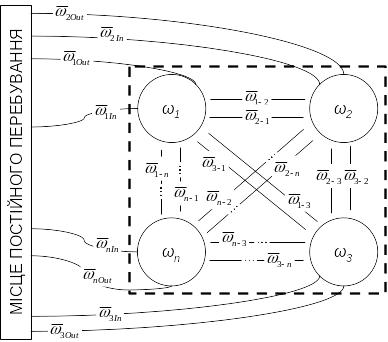
Рисунок 24.1 - Принципова функціональна схема побудови мережевої моделі (графа) системи медичного обслуговування
Для
кожного вузла дозволяються окрім
описаних вище потоків ще вхідний потік
пацієнтів, вихідний потік
(виписка пацієнтів назовні) та внутрішній
потік пацієнтів
з місця лікування у чергу на транспортування
до інших вузлів (рис. 24.2).
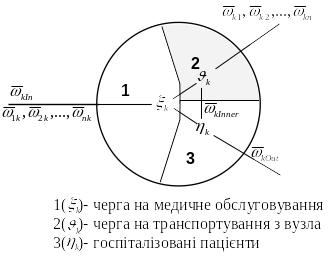
Рисунок 24.2 - Принципова схема k-го вузла медичного обслуговування
Інтенсивності потоків пацієнтів в СМО (як внутрішніх так і зовнішніх) залежать від часу і вважаються випадковими величинами.
Для зручності комп’ютерної реалізації
в математичній моделі використовувався
дискретний спосіб завдання часу,
позначеного як
,
,
=1
доба, MaxDay – тривалість часу
(в добах), протягом якого здійснюється
моделювання. Кожний проміжок часу
може бути розділений на Step дискретних
частин і, таким чином, може розглядатися
як час
,
,
,
де Step – так званий крок
моделювання, котрий є цілим позитивним
числом, частка від ділення на яке одиниці
фактично означає частку проміжку часу
.
Вхідний
потік пацієнтів в СМО можна представити
як суму усіх можливих потоків
у вигляді випадкової функції з незалежними
приростами. Інтенсивність такого
нестаціонарного вхідного потоку
пацієнтів
на момент часу
може бути визначена як:
(24. 2)
де: 
– інтенсивність
нестаціонарного адитивного потоку
пацієнтів j-ої категорії
в момент часу
;
– момент
дискретного часу
,
;
– кількість
категорій пацієнтів.
Потік кожного вузла являє собою потік декількох категорій пацієнтів, що спрямовуються на вузол зовні, кожна категорія пацієнтів в моделі пересувається по унікальній послідовності вузлів обслуговування.
В свою чергу вхідний потік пацієнтів j-ої категорії в момент часу до системи може бути представлений наступним чином:
,
(24.3)
де: 
– частка
пацієнтів j-ої категорії
від загальної кількості осіб з w-м
захворюванням або ураженням
– коефіцієнт
втрат за окремим видом ураження або
коефіцієнт захворюваності, що відповідає
моменту часу
,
;
– початкова
чисельність в момент часу
g-ї групи осіб (військова
частина, угруповання військ, контингент
населення та ін.), медичне забезпечення
яких моделюється;
– кількість
факторів ураження (видів зброї) та
різновидів захворювань на мирний час.
З формули (24.3) виходить, що однорідні за своїми медичними характеристиками пацієнти, що належать до різних груп осіб, вважаються різними категоріями.
Вихідний потік пацієнтів з системи є
нестаціонарним і являє собою суму усіх
потоків
.
Його інтенсивність у момент часу
(
)
позначимо як
:
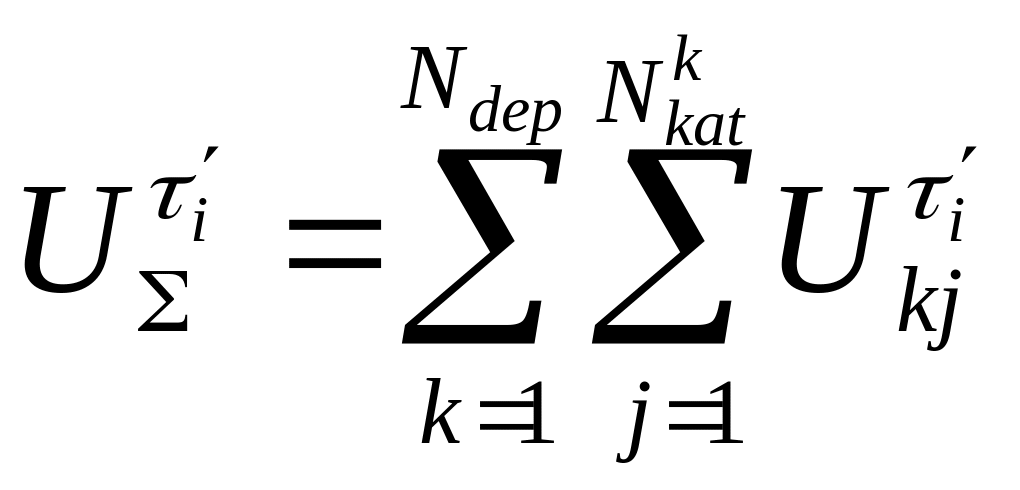(24. 4)
де: 
– інтенсивність
вихідного потоку пацієнтів j-ї
категорії з k-го
вузла в момент часу
;
– кількість
категорій пацієнтів, що спрямовуються
на k-й вузол.
Вихідний потік пацієнтів
j-ої категорії з k-го вузла являє
собою суму елементарних потоків виписки
пацієнтів, що надходили в усі попередні
моменти часу
:
,
(24.5)
(24. 6)
де: 
– кількість
пацієнтів j-ої категорії, що надійшла
на лікування у k-му вузлі в момент
часу q (надходять з черги
);
NFlowOut – кількість можливих станів пацієнтів (можливими станами є повне одужання, смерть та ін.);
– імовірність
виписки пацієнтів j-ої категорії з
k-го вузла у стан f в момент часу
;
– імовірність
виписки пацієнтів j-ої категорії з
k-го вузла у стан f в момент часу
,
який відповідає моменту часу
;
,
де
– максимальний
час лікування пацієнтів j-ої категорії
у k-му вузлі (у добах);
, 
;
(24.7)
b – індекс, що визначає вид моделі виписки, b = 0 для загальної нестаціонарної моделі, b = 1…7 для диференційованої нестаціонарної моделі (цими числами кодуються дні тижня, індекс b обчислюється відповідно до реальної дати надходження пацієнтів спеціальною функцією Delphi).
Інші формули математичної моделі
описують переміщення пацієнтів з черги
k на
медичне обслуговування в чергу
на транспортування з вузла та в місце
остаточного лікування, а також вплив
факторів ризику на транспортні ресурси
вузлів обслуговування та ресурси
робочого часу на надання медичної
допомоги.
Перевагою запропонованої математичної
моделі є те, що вона дозволяє представляти
потоки надходження та виписки пацієнтів
як стаціонарні, так і складні нестаціонарні
процеси. При цьому в моделі (формула 6)
можливе представлення ймовірностей
виписки (
)
у вигляді аналітичних функцій або
дискретного набору ймовірностей.
Для створення аналітичних функцій запропоновано використовувати підбір апроксимаційних рівнянь з використанням функції щільності ймовірності нормального розподілу. Дискретні набори ймовірностей доцільно формувати шляхом побудови запитів до баз даних обліку пацієнтів.
Розроблена математична модель була реалізована в комп’ютерних програмах “Модель системи надання медичної допомоги та етапного лікування” (“Model”) та “Модель закладу охорони здоров’я” (“Hospital”). Відповідно були розроблені алгоритми роботи та реляційна модель бази даних програмного забезпечення.
Важливим питанням комп’ютерної реалізації розробленої математичної моделі виявилась організація зберігання та обробки необхідної для моделювання інформації. Основні етапи переробки інформації під час моделювання та організація її зберігання знайшли відображення в розробленій інформаційній моделі, створеній згідно стандартів інформаційної технології SSADM. Згідно інформаційної моделі, моделювання представляється як комплекс інформаційних задач. Інформаційне моделювання дозволило встановити, що найголовнішою інформаційною задачею, яка повинна вирішуватись під час моделювання, виявилось не саме моделювання як обчислювальний процес, а задачі підготовки та відбору потрібної для моделювання інформації. Вирішальна роль якісного виконання цих інформаційних задач була підтверджена в експериментах по перевірці точності роботи моделі.
25. Писаренко Т.М. Шляхи підвищення ефективності використання фінансових ресурсів у системі охорони здоров ’я . [Електронний ресурс] / Писаренко Т.М. – Тернопіль: БНТУ, 1999. – 116 с. - Режим доступу: http://studentam.kiev.ua
Важливим етапом у розробці планів розвитку охорони здоров ’ я на всіх рівнях народного господарства є планування стаціонарної медичної допомоги і раціонального розміщення мережі лікувальних установ.
Організаційні форми надання медичної допомоги населенню , структура лікувальних установ і їх розміщення залежать від рівня й характеру захворюваності , чисельності, статевого та професійного складу населення і особливостей його розселення в окремих районах країни . Плануванню стаціонарної допомоги повинна передувати робота із нагромадження необхідних нормативів , які використовують для планування розвитку на конкретній території лікарень , пологових будинків , диспансерів та інших стаціонарних установ. До таких нормативів слід віднести : кількість випадків госпіталізації на 1000 жителів ; тривалість лікування хворого в стаціонарі ; кількість днів використання лікарняного ліжка за рік; кількість лікарняних ліжок на 10 тис. жителів.
Загальний норматив кількості випадків госпіталізації виражають сумою нормативів із спеціалізованих видів медичної допомоги. Важливим вихідним показником, який використовують для визначення потреби населення в стаціонарній допомозі , є норматив середнього перебування хворого на ліжку. На величину цього показника, як відомо , впливає ряд факторів : склад госпіталізованих хворих, важкість їх захворювань , терміни госпіталізації , кваліфікація лікарів , забезпечення населення лікувальними ліжками , рівень і якість догоспітального обстеження хворих, діагностика захворювань і ряд інших .
Г . А. Попов запропонував
визначати середню тривалість
госпіталізації
за формулою:
,
(25.1)
де
–
кількість ліжко- днів , які провів
хворий за m - ою спеціальністю;
– кількість хворих, госпіталізованих протягом року за m - ою спеціаль -ністю;
–
кількість виписаних із стаціонару
хворих за m - ою спеціальністю;
–
чисельність померлих хворих у стаціонарі
за m - ою спеціальністю.
Середні терміни лікування хворих у стаціонарі можуть бути скорочені шляхом удосконалення діагностики на догоспітальному етапі (в першу чергу на амбулаторно-клінічному ) та вдосконалення взаємозв’язку поліклінік і стаціонарів . Для визначення потреби населення в стаціонарній допомозі необхідно знати і такий норматив, як кількість днів використання ліжка за рік. Цей норматив встановлює Міністерство охорони здоров ’ я розрахунково – окремо для міських і сільських лікувальних установ із уточненням згаданого показника за окремими спеціальностями. Для міських стаціонарів цей норматив становить у середньому 340 днів , для сільських – 310. Низькі показники кількості днів використання лікарняного ліжка за рік не тільки ведуть до зниження забезпеченості населення
стаціонарною медичною допомогою , а й завдають значних економічних збитків. Затрати на ліжко, яке не займає хворий, лише на 20–25% менші від затрат на зайняте ліжко . У практиці лікувальних установ показник кількості днів використання ліжка характеризує діяльність не тільки окремих стаціонарів , а й лікарень , диспансерів, пологових будинків на окремих адміністративних територіях . Розрахувати показник кількості днів використання лікарняного ліжка можна шляхом ділення кількості ліжко- днів , які провели тут усі хворі, на відповідну кількість середньорічних ліжок. При цьому оцінку й порівняння показника використання ліжкового фонду в окремих лікарнях доцільно проводити з урахуванням спеціалізації ліжок, оскільки норматив даного показника за різними спеціальностями неоднаковий. У практиці планування при аналізі діяльності лікувальних установ використовують показник «обіговість ліжка», що характеризує чисельність хворих, які перебувають на лікарняному ліжку протягом року . Обіговість ліжка може бути отримана в результаті ділення половини суми чисельності хворих, які лягли в лікарню, виписані звідти або померли , на середньорічну кількість лікарських ліжок. При наявності даних про рівень захворювання населення, про кількість випадків госпіталізації на 1000 жителів, середню тривалість лікування хворого в стаціонарі, кількість днів роботи ліжка за рік і ряду інших показників ( обіговість ліжка, народжуваність , чисельність і статево- віковий склад населення з розподілом на міське та сільське , смертність населення) можна приступити до визначення потреби в лікувальних установах на той чи інший період . При складанні плану розвитку лікувальної важливо знати забезпеченість цим видом медичної допомоги міського населення, в тому числі робітників промислових підприємств, будівництва і транспорту . Необхідно визначити відповідність потреби цієї категорії працівників фактичному забезпеченню як у цілому стаціонарною допомогою , так і окремими її спеціалізованими видами.
При розробці плану охорони здоров ’ я на селі , визначенні розмірів і побудови мережі сільських медичних установ ще в більшій мірі слід враховувати ряд особливостей , що так чи інакше впливають на розвиток і організацію медичної допомоги населенню , в тому числі густину населення, географічні особливості, специфіку сільськогосподарського виробництва та інші умови . Для визначення потреби населення в стаціонарній допомозі можна використовувати показники чисельності населення, відсотка госпіталізації , середньої кількості днів перебування хворого на ліжку, середньої кількості днів використання ліжка за рік. Визначити диференційовану потребу в лікарняних ліжках можна за формулою:
,
(25.2)
де – необхідна кількість середньорічних ліжок на 1000 жителів ;
– рівень захворюваності від звернення до лікаря на 1000 жителів ;
– відсоток відбору на ліжко від чисельності тих , хто звернувся до лікаря ;
–
середня кількість днів перебування
хворого на ліжку ;
– середня кількість днів використання ліжка за рік.
Для розрахунку потреби в лікувальній мережі населення певної території може бути використана така формула :
,
(25.3)
де
- нормативна кількість
ліжок на 1000 жителів ;
–
норматив випадків госпіталізації
на 1000 жителів (міських і сільських).
Наявність даних про потребу населення в окремих видах спеціалізованої медичної допомоги дає можливість оцінити і визначити напрямок у спеціалізації ліжкового фонду , раціональність його розміщення в лікувальних установах з урахуванням функціональних обов ’ язків останніх . Використання при плануванні нормативів потреби в різних видах спеціалізованої медичної допомоги потребує врахування місцевих умов і особливостей , що, в свою чергу, визначає застосування тих чи інших організаційних форм лікувально - профілактичної допомоги населенню . Це стосується насамперед вузьких спеціальностей ( нейро-хірургія, серцево- судинна хірургія, кардіологія , ендокринологія , гематологія). При організації вузькоспеціалізованих служб необхідно враховувати потребу в них не тільки жителів даної території , а й населення, яке живе поблизу.
26. Биджиев В.З. МЕТОДЫ НЕЛИНЕЙНОЙ ДИНАМИКИ ДЛЯ ДВУХУРОВНЕВОГО МОДЕЛИРОВАНИЯ ЗАДАЧ УПРАВЛЕНИЯ РЕСУРСАМИ ЗДРАВООХРАНЕНИЯ автореф.дис. на соискание ученой степени кандидата экономических наук: спец. 08.00.13 –математические и инструментальные методы экономики / Биджиев В.З.- Иваново, 2012. – 67, [1] c.
Научная разработка финансово-экономических и управленческих систем в здравоохранении остаётся весьма актуальной. Наиболее опасным недостатком существующих методик стала вынужденная необходимость искусственно занижать реальный спрос на медицинские услуги и укладывать его в возможности бюджета. Такой подход приводит к заведомому искажению реально необходимых показателей оказываемой медицинской помощи и не позволяет достоверно оценить необходимые объёмы базовых программ, размеры страховых тарифов и т.п.
Для реализации целей диссертационного исследования осуществлена оценка реальных возможностей инструментария статистического анализа для прогнозирования временных рядов, построенных на основе статистических данных ежедневного количества обратившихся за медицинской помощью за период с 01.01.2007 года по 27.12.2009 год в Государственное республиканское учреждение здравоохранения «Карачаево-Черкесской республиканской больницы». Выявленная слабая адекватность реальным исходным данным классических методов прогнозирования, базирующихся на трендах и автокорреляции, обусловила необходимость выбора такой математической модели прогнозирования, которая базируется на инструментарии клеточных автоматов и теории нечетких множеств. Дается содержательное описание концепции двухуровневого подхода к моделированию эволюционных социально-экономических процессов и систем, показатели которых не подчиняются нормальному закону распределения. Для них характерны множественность и противоречивость целей и критериев, стохастичность, интервальность или нечеткость значений исходных данных и хаотичность структуры связей. Математическая модель верхнего уровня – это модель теории оптимизации, на базе которой строится и обосновывается наиболее целесообразное управление распределением инвестиций. На нижнем уровне осуществляется моделирование исходных данных для модели верхнего уровня. Графическое представление двухуровневого подхода к моделированию инвестиционных решений в здравоохранении приведено на рисунке 26.1.
Автором разработана математическая формализация концептуальной модели, базирующаяся на методах нелинейной динамики.
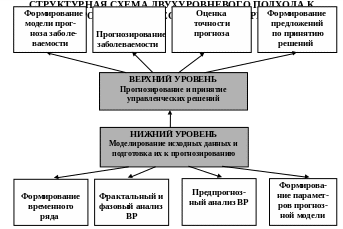
Рисунок 26. 1 - Структурная схема двухуровневого подхода к моделированию инвестиционных решений в здравоохранении.
На нижнем уровне предложен достаточно общий подход и инструментарий использования предпрогнозных фрактальных характеристик временных рядов как для оценки их прогнозируемости, так и для качественной оценки устойчивости и тенденции в динамике развития процессов планирования медицинских ресурсов.
На верхнем уровне моделируется спрос на медицинские услуги в регионе. Прогнозирование базируется на линейных клеточных автоматах, а также предполагает использование операции агрегирования.
Алгоритм прогнозирования на базе клеточного автомата реализуется в системном единстве с процессом моделирования долговременной памяти и завершается получением прогноза заболеваемостей, включая валидацию (оценивание погрешности результата). Алгоритм реализации двухуровневой состоит из следующих шести этапов.
Этап 1. Использование статистических методов и визуализация для предварительного анализа данного временного ряда на предмет выявления наличия или отсутствия тяжелых хвостов, трендов, циклических или сезонных компонент и др.
Этап 2. Фрактальный анализ данного
временного ряда с целью установления
в нем долговременной памяти, включая
оценку ее глубины, а также выявления в
поведении временного ряда таких
характеристик и тенденций, как
трендоустойчивость или, наоборот,
хаотичность, персистентность или
антиперсистентность и др. Вычислительная
часть фрактального анализа базируется
на алгоритме
-
анализа. Оценки, получаемые на выходе
этого этапа, имеют числовую природу:
наиболее адекватным является их
представление в терминах и понятиях
нечетких множеств.
Этап 3. Преобразование числового временного ряда в лингвистический временной ряд с целью обеспечить возможность применить квазигенетический алгоритм, работающий с комбинаторными конфигурациями, составляющими собой структуру лингвистического временного ряда и его терм-множество
Этап 4. Построение определяемой данным лингвистическим временным рядом генетической памяти клеточного автомата состоит из подэтапов:
-
формирование множества
всех
-конфигураций,
содержащих в полученном лингвистическом
временном ряде,
,
где
- глубина памяти этого лингвистического
временного ряда;
- вычисление частот и частостей переходов - конфигураций из в состояния-термы.
Этап 5. Формирование прогноза для рассматриваемых числового и лингвистического временного ряда путем реализации «мягких вычислений» на базе построенной памяти клеточного автомата:
- получение прогноза в виде нечеткого лингвистического множества;
- преобразование нечеткого лингвистического множества в числовое нечеткое множество, которое при необходимости с помощью процедуры дефазификации можно перевести в четкий числовой прогноз.
Этап 6. Валидация, т.е. получение оценок погрешности для полученного прогноза числового и лингвистического временных рядов.
Все этапы предлагаемой прогнозной модели были осуществлены на 10 временных рядах числа зарегистрированных больных в 9 разно профильных отделениях и итого по всем отделениям республиканской больницы КЧР за 2007-2009 гг.
Вторая группа проблем исследования связана с детальным предпрогнозным анализом временных рядов заболеваемостей с использованием математического аппарата фрактального и фазового анализа.
Исходными статистическими данными в
настоящем исследовании являются
подневные временные ряды
,
где индексом
перенумерованы годы рассматриваемого
периода длиной
лет, а
– количество жителей данного населенного
пункта, обратившихся за медицинской
помощью в
-й
день года
.
С целью анализа динамики наблюдаемых количеств заболевания были введены обозначения для всех десяти временных рядов:
,–
терапевтическое отделение,
,–
отделение неврологии,
,–
отделение хирургии (взрослое),
,–
нейрохирургическое отделение,
,–
отделение ЛОР (взрослое),
,–
глазное отделение,
,–
отделение пульмонологии,
,–
отделение кардиологии,
,–
детское анестезиолого-реанимационное
отделение,
,–
итого по всем отделениям.
Рассматривая численные значения статистических показателей всех 10 временных рядов (ВР), получаем:
– значения коэффициента асимметрии А по абсолютной величине далеки от нуля, т. е. эмпирические распределения не симметричны и относятся к классу распределений с «тяжелыми хвостами», в силу чего для их анализа и прогноза классическая методология прогнозирования приемлема в малой степени.
– коэффициент эксцесса Е отклоняется
в меньшую сторону от значения коэффициента
эксцесса, присущего нормальному
распределению, этот факт объясняется
тем, что область определения эмпирического
распределения для рассматриваемых
рядов в большинстве случаев принадлежит
окрестности
,
где М – математическое ожидание,
- среднеквадратическое отклонение.
– большинство рассмотренных ВР отличаются
повышенной вариабельностью, а именно,
коэффициент вариации
принимает значения из интервала (0,5; 1).
Для
оценки глубины памяти временных рядов
(численная оценка одной из фрактальных
характеристик временного ряда, обладающего
долговременной памятью)
заболеваемостей,
автором используется алгоритм
последовательного
анализа.
Исследована иерархия цикличности временных рядов заболеваемостей.
Для различных экономических временных
рядов достаточным является построение
фазовой траектории в фазовом пространстве
размерности
.
Рассматриваем эту фазовую траекторию
в виде траектории, т.е. последовательности
точек, перенумерованных индексом
,
где
-
ая точка имеет координаты: абсцисса –
,
ордината –
,
.
В траектории каждая соседняя пара точек
соединена звеном, т. е. отрезком или
кривой. В этой траектории выделяем такие
ее части, которые называются термином
«квазициклы». Квазицикл временного
ряда означает наличие в нем таких
циклических компонент, которые различаются
между собой по длине и периодичности.
Отметим две особенности этих квазициклов.
Во-первых, практически для каждого
квазицикла
его длина
,
чаще всего составляет 4 недели, т.е.
несколько не достигает месячный период
времени. С учетом этого факта можно
говорить о “квазимесячной” цикличности
понедельных временных рядов
,
.
Во-вторых, для этих квазициклов существует
дрейф, который имеет циклическую природу
сезонности, что и обуславливает
существование годового цикла на третьем
уровне иерархии.
Иерархию цикличности временных рядов заболеваемости составляют подневные циклы 1- недельной длительности, понедельные квазициклы месячной (квазимесячной) длительности и помесячные квазициклы “сезонной” длительности. На каждом из трёх уровней иерархии всякое звено у подавляющего большинства циклов и квазициклов имеет направление вращения по часовой стрелке. Последнее имеет важное значение, когда модель прогнозирования базируется на разложении фазовых траекторий на квазициклы. Таким образом, из выявленной трёхуровневой иерархии цикличности рассмотренных ВР вытекает принципиальная возможность прогнозирования количества обращений за медпомощью на каждом из трех уровней: краткосрочный (подневный), среднесрочный (понедельный или помесячный) и долгосрочный (сезонный) прогнозы.
Содержательное описание модели иерархичности циклической компоненты рассматриваемых временных рядов можно представить следующим образом:
1. Нижний (первый) уровень иерархии составляют такие отрезки подневного временного ряда, которые имеют длительность одна неделя, т.е. нижний уровень состоит из квазициклов «недельной» длительности.
2. Средний (второй) уровень составляют такие квазициклы понедельного (т.е. агрегированного с недельным интервалом) временного ряда, длительность которых составляет порядка одного месяца; эта длительность претерпевает незначительные колебания в зависимости от сезона года. Иными словами, средний уровень состоит из квазициклов «месячной длительности».
3. Верхний (третий) уровень составляют такие квазициклы помесячного временного ряда длительностью порядка одного года. Иными словами, верхний уровень состоит из квазициклов «годичной» длительности. Структура этих квазициклов обусловлена факторами сезонности.
Разработана методика выявления и анализа циклической компоненты временных рядов количества людей, обратившихся за медицинской помощью, на базе фазовых траекторий и разложения их на квазициклы. Получаемая на базе этого разложения предпрогнозная информация представляет собой дополнительное знание о закономерностях динамики рассматриваемого временного ряда. Это знание может быть использовано для повышения точности и надежности нечеткого прогноза, получаемого на выходе клеточного автомата.
Выявлена трехуровневая иерархия циклической компоненты временных рядов заболеваемости. Структуру этой иерархии составляют подневные циклы 1-недельной длительности, понедельные квазициклы месячной (квазимесячной) длительности и помесячные квазициклы “сезонной” длительности. Выявленная трёхуровневая иерархия цикличности рассмотренных ВР дает принципиальную возможность прогнозирования количества обращений за медпомощью на каждом из трех уровней: краткосрочный (подневный), среднесрочный (понедельный или помесячный) и долгосрочный (сезонный) прогнозы.
Третья группа проблем исследования связана с методикой прогнозирования спроса на медицинские услуги в регионе на базе математической теории клеточных автоматов.