
- •0Министерство образования и науки российской федерации
- •Факультет пгс-ф. Кафедра асп курсовой проект
- •Москва 2013 г. Оглавление
- •Раздел I. Конструирование сборных железобетонных конструкций пятиэтажного здания.
- •Раздел II. Монолитное балочное перекрытие с плитами, работающими в одном направлении
- •Исходные данные для проектирования
- •Раздел I. Конструирование сборных железобетонных конструкций пятиэтажного здания.
- •1.1.Компоновка конструктивной схемы сборного перекрытия
- •1.2. Расчет ребристой плиты
- •1.2.1. Расчёт ребристой плиты по предельным состояниям первой группы
- •1.2.2. Расчет плиты по предельным состояниям второй группы.
- •1.2.3. Проверка прочности плиты в стадии изготовления
- •1.2.4. Расчет прочности плиты в стадии транспортирования
- •1.2.5. Расчет прочности плиты в стадии монтажа
- •1.2.6. Расчет монтажной петли
- •1.2.7. Конструирование плиты
- •1.3. Проектирование ригеля
- •1.3.1. Расчет ригеля в стадии эксплуатации
- •1.3.2. Проектирование стыка ригеля с колонной.
- •1.3.3. Построение эпюры материалов в ригеле и конструирование ригеля.
- •1.4. Проектирование сборной колонны.
- •1.4.1. Расчет прочности колонны среднего ряда в стадии эксплуатации
- •Продольные силы и моменты в колоннах по этажам
- •1.5. Проектирование отдельного фундамента под среднюю колонну
- •1.5.1.Определение размеров фундамента
- •1.5.2.Расчет прочности подошвы фундамента
- •1.5.3.Конструирование фундамента
- •Раздел II. Монолитное балочное перекрытие с плитами, работающими в одном направлении.
- •2.1. Компоновка конструктивной схемы монолитного перекрытия.
- •2.2. Проектирование монолитной плиты перекрытия.
- •2.2.1. Расчет плиты перекрытия в стадии эксплуатации
- •2.2.2. Размеры и расчетные пролеты элементов перекрытия.
- •2.2.3. Сбор нагрузок и определение усилий в плите.
- •2.2.4. Прочность нормальных сечений плиты (подбор арматуры).
- •2.2.5. Конструирование плиты.
- •2.3. Проектирование кирпичного столба.
- •2.3.1. Сбор нагрузок и определение усилий в столбах.
- •2.3.2. Расчет прочности столба первого этажа.
- •2.4. Расчет отдельного ступенчатого фундамента.
- •2.4.1. Определение размеров фундамента.
- •2.4.2. Расчет прочности фундамента.
- •Используемая литература.
1.2.2. Расчет плиты по предельным состояниям второй группы.
• Геометрические характеристики расчетного сечения.
Расчетное сечение таврового профиля с полкой в сжатой зоне. Бетон тяжелый класса В30, Rb = 17 МПа (17∙ 103 кН/м2). Размеры сечения h=30 см, , ширина ребра b =14 см, , рабочая высота сечения ho = 27 см, (а = Зсм).
Площадь бетона
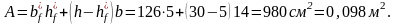
Коэффициент приведения
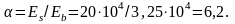
Площадь приведенного сечения:
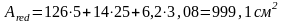 ≈0,09991м2.
≈0,09991м2.
Статический момент приведенного сечения относительно нижней грани:
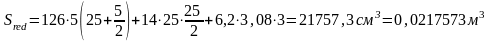
Расстояние от оси, проходящей через нижнюю грань продольного ребра до центра тяжести приведенного сечения:
у0 = 21757,3/999,1 = 21,8 см.
Момент инерции приведенного сечения относительно центра тяжести сечения:
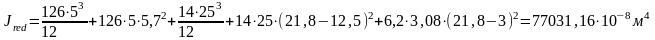
Момент сопротивления приведенного сечения по нижней зоне:
Wred = Jred / уо = 77031,16/21,8=3533,5 см3= 0,0035335 м3,
то же по верхней зоне:
W|red = Jred / (h-уо)= 77031,16/(30-21,8) =9394 см3= 0,009394 м3,
Упругопластический момент для таврового сечения с полкой в сжатой зоне для расчетов в стадии эксплуатации при γ = 1,3
Wp1 = γ Wred =1,3∙3533,5=4593,55 см3 = 0,00459335 м3.
То
же для таврового сечения с полкой в
растянутой зоне для расчетов в стадии
изготовления при:
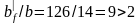 ,
коэффициент γ=1,15
,
коэффициент γ=1,15
W/p1 = γ W/red =1,15∙9394=10803,1 см3 = 0,0108031 м3.
Коэффициент γ определяется по таблице 11 приложения.
• Установление уровня предварительного натяжения арматуры.
Уровень предварительного напряжения для горячекатаной и термомеханически упрочненной арматуры назначается так, чтобы соблюдались условия:
σsp ≤ 0,9Rs,ser; σsp ≥ 0,3Rs,ser
Коэффициент точности натяжения арматуры (учет возможных отклонений) при определении потерь предварительного натяжения и расчетах по второй группе предельных состояний принимется равным γsp=l,0.
Предварительно назначим уровень преднапряжения 80% от Rsn
σsp =0,8Rsp=0,8∙800=640 МПа.
• Расчет потерь предварительного напряжения арматуры.
Расчет потерь производится в соответствии со СНиП при коэффициенте точности натяжения арматуры уsp = 1,0.
• Первые потери.
∆σsp1 - потери от релаксации напряжений в стержневой арматуре А800 при электротермическом способе натяжения
∆σsp1 = 0,03σsp = 0,03∙ 640 = 19,2 МПа,
∆σsp2 - потери от температурного перепада между натянутой арматурой и упорами не учитываются, так как форма пропаривается в пропарочной камере вместе с изделием, ∆σsp2=0,
∆σsp3 - потери от деформации формы при неодновременном натяжении арматуры в расчетах не учитываются, так как уже учтены в расчете удлинений арматуры, ∆σsp3=0
∆σsp4 - потери от деформации анкеров при электротермическом способе натяжения учтены в расчете полных удлинений арматурных стержней и поэтому равны нулю, ∆σsp4=0.
∆σsp5 -потери от усадки бетона.
Для бетонов В35 н ниже относительная деформация усадки бетона εb,sh= 0,0002
∆σsp5 = εb,sh ∙ Еs = 0,0002 ∙ 20 ∙ 104= 40 МПа.
∆σsp6 -потери от ползучести арматуры определяются по формуле:
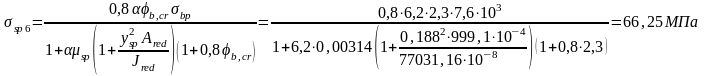 Здесь
Здесь
• коэффициент приведения ɑ = Es /Еb = 6,2;
• эксцентриситет силы обжатия P1 относительно центра тяжести приведенного сечения еsp= уо -а =21,8 - 3 = 18,8 см =0,188 м;
• коэффициент армирования сечения (без учета ненапрягаемых стержней)
• μsp=Asp/A=3,08/980=0,00314;
• коэффициент ползучести бетона φsp=2,3; находится по таблице 10 приложения для бетона ВЗО и влажности 40-75%;
Первые потери преднапряжения равны:
∆σsp(1)= ∆σsp1+∆σsp2+∆σsp3+∆σsp4=19,2+0+0+0 = 19,2 МПа.
Начальное усилие обжатия с учетом первых потерь
P1 = Аsp(σsp -∆σsp(1)) =3,08∙ 10-4(640 - 19,2)103 = 191,2 кН.
Максимальное сжимающее напряжение в бетоне при обжатии силой P1 на уровне крайнего нижнего волокна, у = 0,188+0,03=0,218 м, без учета влияния собственного веса плиты:

Согласно /6/, передаточная прочность бетона Rbp назначается не менее 15 МПа и не менее 50% прочности от класса бетона. Принимаем Rbp= 15 МПа. Сжимающие напряжения в бетоне от силы P1 в стадии предварительного обжатия не должны превышать 90% от передаточной прочности RbP
σbp=12,1 МПа < 0,9Rbp = 0,9∙15 = 13,5 МПа. Требование выполняется. Определим напряжения в бетоне с учетом разгружающих напряжений от веса плиты на уровне центра тяжести продольной арматуры, то есть, при уо = еор = 0,188 м. Из таблицы 1 нагрузка от веса 1 м2 плиты принята 2500 Н. Изгибающий момент от собственного веса плиты вычислен при расчетном пролете 10= 5,56 м.
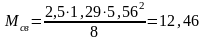 кН∙м,
кН∙м,
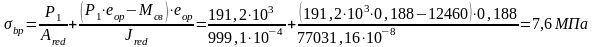
Вторые потери
∆σsp(2)= ∆σsp5+∆σsp6=40+66,25=106,25 МПа
Полные потери
∆σsp= ∆σsp(1)+∆σsp(2)=19,2+106,25=1125,45 МПа>100 МПа.
Принимаем полные потери
∆σsp= 125 МПа
Напряжения в напрягаемой арматуре после проявления всех потерь
σsp2= 640-125=515 МПа
Усилие обжатия с учетом полных потерь
Р2 = 3,08∙10-4(640 – 125)103 ≈158,6 кН.
• Расчет трещиностойкости плиты
Исходные данные. Коэффициент надежности по нагрузке γf =1 и, соответственно, расчетный момент равен нормативному Мн =52,18 кНм, момент сопротивления приведенного сечения по нижней зоне Wred =3533,5 см3, Wpl=4593,55 см3, усилие обжатия с учетом полных потерь Р2 = 158,6 кН, эксцентриситет силы обжатия еор= 0,188 м, r=Wred/Ared= 3533,5/999,1 = 3,54 см, напряжения в напрягаемой арматуре после проявления всех потерь σsp2= 515 МПа.
Условием необразования трещин является соблюдение условия:
Mn≤Mcrc
Момент, соответствующий образованию трещин Mcrc определяем по приближенному способу ядровых моментов:
Mn≤Mcrc=Rbt,serWpl+Mrp
где:
Mrp=P2(еор +r)=158,6(0,188+0,0354)=35,43 кНм.
Rbt,ser ∙Wpl = 1,75 ∙103∙4593,55∙10-6= 8,04 кНм.
Mcrc = 8,04+ 35,43= 43,47 кНм < Мн = 52,18 кНм.
Условие не выполняется, трещины в растянутой зоне образуются. Необходим расчет по раскрытию нормальных трещин.
• Ширина раскрытия нормальных трещин продольных ребер
Исходные данные. Предельная ширина раскрытия трещин аcrc,ult, для конструкций к которым не предъявляются требования непроницаемости, при арматуре А800, не должна превышать 0,2 мм при продолжительном раскрытии и 0,3 мм при непродолжительном раскрытии. Так как конструктивная ненапрягаемая арматура 2Ø8 В500, As =1,01см2 в определении геометрических характеристик не учитывалась, то усилие Р2 приложено в центре тяжести нижней арматуры, еsp = 0,0; напрягаемая арматура 2Ø14 А800; Asp = 3,08 см2, Р2=158,6 кН, изгибающие моменты от нормативных нагрузок: от полной нормативной нагрузки Мn = 52,18 кНм, от постоянной и длительной Мдл =45,04 кНм.
Расчет по раскрытию трещин производят из условия:
acrc≤ acrc,uit
где acrc е - ширина раскрытия трещин от внешней нагрузки, acrc,uit - предельно допускаемая ширина раскрытия трещин.
Ширина раскрытия трещин от внешней нагрузки вычисляется по формуле:
acrc =φ1 φ2ψsσsls/Es
Приращение напряжений в растянутой арматуре для прямоугольных, тавровых и двутавровых сечений разрешается принимать при z ≈ 0,7ho, если выполняется условие acrc≤ acrc,uit или определять по по формуле z = ζho, где коэффициент ζ принимется по таблице 20 приложения.
Ширина раскрытия трещин
от кратковременного действия всей нагрузки Мn = 52,18 кНм.
Для определения коэффициента ζ по таблице, находим дополнительные парапметры:
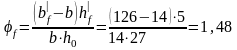

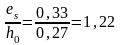
Коэффициентαs1 для всех видов арматуры кроме канатной равен:
αs1 =300/Rb,ser
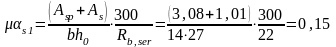
Находим по таблице, что коэффициент ζ≈0,85
Z=ζho = 0,85∙0,27= 0,23 м.
Вычисляется эквивалентный момент от внешней нагрузки и усилия преднапряжения, причем знак плюс в формуле берется, если направления моментов совпадают и минус, если направления противоположны
Ms= М± Реор =52,18±0,0=52,18 кНм.
Приращение напряжений от полной нормативной нагрузки Мп = 52,18 кНм.
В расчетах учитываем продольную ненапрягаемую арматуру каркасов 2Ø8 В500
As=1,01см2

Проверяем условие
σsp2+ σs=515+166,9=681,9<Rs,ser=800МПа. Условие соблюдается.
• φ1 - коэффициент, учитывающий продолжительность действия нагрузки:
φ1= 1,0 при непродолжительном действии нагрузки,
φ1 = 1,4 при продолжительном действии нагрузки
• φ2- коэффициент, учитывающий профиль арматуры:
φ2 = 0,5 для стержневой арматуры периодического профиля и канатов,
φ2 =0,8 для гладкой арматуры,
• ψs- коэффициент, учитывающий неравномерность распределения деформаций растянутой арматуры между трещинами. Допускается принимать ψs =1, если выполняется условие acrc≤ acrc,uit ,
• ls - базовое расстояние между трещинами,
ls=0,5Abtds/(Asp+As), причем должны выполняться условия 10ds≤ls≤40ds и 100мм≤ls≤400мм
Abt=kytb= 0,9∙0,114∙0,14 = 0,0144м3, где
yt=Sred/(Ared+P2/Rbt,ser)= 0,0217573/(0,0991+158,6/1,75∙103) = 0,114 м.
ds= (2∙142+2∙82)/(2∙14+2∙8) =11,82 мм,
ls = 0,5∙0,0144∙0,0118/(3,08+1,01) ∙10-4 =210 мм.
Базовая ширина раскрытия трещин должна удовлетворять условиям
10 ds =10∙11,82=118,2 мм≤ls =210мм≤40 ds =40∙11,82=472,8 мм.
Окончательно принимаем ls = 210 мм.
Раскрытие трещин от кратковременного действия полной нормативной нагрузки
acrc2=φ1φ2ψsσs ls/Es= 1,0 ∙0,5 ∙1,0 ∙166,9 ∙103 ∙0,21/20 ∙107= 0,088 мм.
Ширина раскрытия трещин от кратковременного
действия длительной нагрузки.
Исходные данные. Мп,дл=45,04 кНм; φf=1,48; φ1=1,0; φ2=0,5; ψs=1; es= Мп,дл/P2=0,284; es/h0=1,22; µαs1=0,15. По таблице 20 приложения ζ=0,85;z=0,85 ∙0,27=0,23;
Приращение напряжений от постоянной и длительной нормативной нагрузки
Ms= М± Реор =45,04-0,0=45,04 кНм.

Ширина раскрытия трещин равна
acrc3=φ1φ2ψsσs ls/Es=1,0 ∙0,5 ∙1,0 ∙91 ∙103 ∙0,21/20 ∙107= 0,048 мм.
Ширина раскрытия трещин при
продолжительном действии длительной
Исходные данные. Мп,дл=45,04 кНм; φf=1,48; φ1=1,4; φ2=0,5; es= Мп,дл/P2=0,284; es/h0=1,22; µαs1=0,15; ζ=0,85; z=0,85 ∙0,27=0,23;
Ширина раскрытия трещин при φ1=1,4:
acrc1=1,4 ∙0,5 ∙1,0 ∙91 ∙103 ∙0,21/20 ∙107= 0,067 мм.
Итоговая ширина раскрытия трещин
• при непродолжительном действии нагрузки
acrc= acrc1+ acrc2- acrc3= 0,067+0,088-0,048 = 0,107 мм < acrc,uit= 0,3 мм,
• при продолжительном действии нагрузки
acrc= acrc1=0,067 мм< acrc,uit=0,2 мм.Условия выполняются.
• Расчет прогибов плиты
Расчет по прогибам производят из условия
f ≤ fult
Здесь f - прогиб от внешней нагрузки, fult- предельно допустимый прогиб.
Для элементов постоянного сечения, работающих как свободно опертые или консольные балки, прогиб допускается определять по формуле
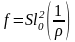 ,
,
где
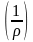 -
полная кривизна в сечении с наибольшим
моментом.
-
полная кривизна в сечении с наибольшим
моментом.
Для участков с трещинами в растянутой зоне полная кривизна определяется:
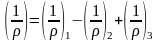 ,
,
где
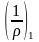 -
кривизна
от непродолжительного действия всей
нагрузки,
-
кривизна
от непродолжительного действия всей
нагрузки,
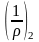 -
кривизна от непродолжительного действия
постоянных и длительных нагрузок,
-
кривизна от непродолжительного действия
постоянных и длительных нагрузок,
 -кривизна
от продолжительного действия постоянных
и длительных на-
-кривизна
от продолжительного действия постоянных
и длительных на-
грузок,
S - табличный коэффициент, принимаемый по табл. 12 приложения.
Кривизна от непродолжительного действия всей нагрузки
Исходные данные. Действующий момент от полной нормативной нагрузки Mn=52,18 кНм; рабочая высота сечения h0=27 см; ;b=14см; Р2=158,6 кН.
Для элементов прямоугольного таврового и двутаврового профилей допускается вычислять кривизну по упрощенной формуле при выполнении условий:
• <0,3ho =0,3∙27=8,1 см, условие выполняются,
• а's = 0 см < 0,2 ho =0,2∙27=5,4 см, условие выполняются.
Вычисляем кривизну по упрощенной формуле
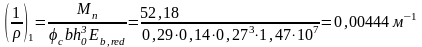
где:
φc - определяется по таблице 21 приложения по параметрам:
φf = 1,48 из предыдущего раздела; es/h0=0,33/0,27 = 1,22;
при f ≤ fult допускается принимать ψs =1 и соответственно, вычисляем
Eb,red= Rb,ser /εb,red=22∙103/15∙10-4=1,47∙107кН/м2;
αs2= αs1= Es/ Eb,red= 20∙107/1,47∙107=13,6,
µαs2= (Аsp+ Аs) αs1/bh0=13,6(3,08+1,01) ∙10-4/0,14 ∙0,27=0,147,
Находим φc = 0,29 и вычисляем кривизну.
Кривизна от непродолжительного действия
постоянных и длительных нагрузок
Исходные данные. Действующий момент от постоянной и длительной нормативной нагрузки Mn,дл=45,04 кНм; h0=27 см; b=14 см; As=3,08∙10-4м2; Р2=158,6 кН; Eb,red=1,47∙107кН/м2;
µαs2=0,147; По таблице 21приложения φc=0,29.
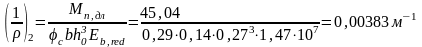
Кривизна от продолжительного действия
постоянных н длительных нагрузок
Исходные данные. Mn,дл=45,04 кНм; Eb,red= Rb,ser /εb,red=22∙103/28∙10-4=0,78∙107кН/м2; µαs3=0,277 es/h0=1,22 φf = 1,48 По таблице φc=0,43.
Вычисляем кривизну по упрощенной формуле
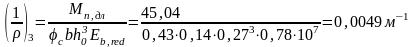
Полная кривизна
=0,00444-0,00383+0,0049=0,00551м-1
Прогиб плиты
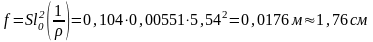
fult=l/200=5,54/200=0,028 м=2,8 м при пролете элемента 6 м.
f =1,76 см < fult=2,8 см
Условие удовлетворяется, пересчет по уточненной формуле не производим.
