Введемо позначення
Диференціальне рівняння приймає вигляд
Таким чином, маємо систему, що складається з трьох рівнянь першого порядку
У
матричному вигляді ця система має вигляд
то мережа
Отже,
оператором системи буде
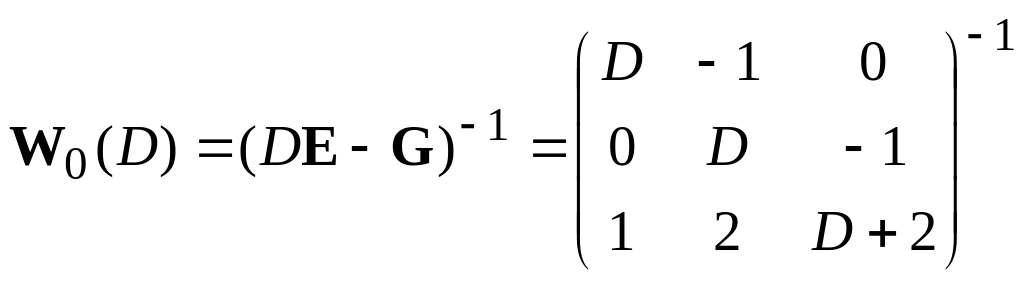
Після звернення матриці, отримаємо
.
Помножимо отриманий вираз справа на вхідну матрицю, отримаємо матричну передавальну функцію
.
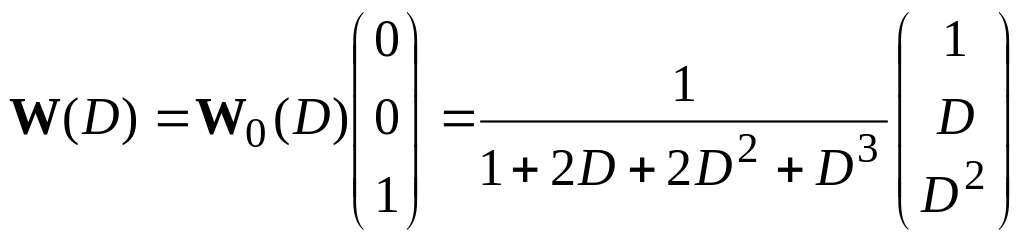Бачимо, що отримана передавальна функція відрізняється від тієї, яку ми
отримали в першому варіанті, оскільки ми змінили позначення для вектора стану. Проте, позначення для ми зберегли, залишилася незмінною і передавальна функція для цієї компоненти.
Принцип максимуму Понтрягіна. Стійкість лінійних систем. Методи аналізу стійкості лінійних об'єктів і систем. Статистичні методи дослідження лінійних систем.
У ряді практичних завдань на безліч управлінь накладаються деякі істотні обмеження у вигляді нерівностей. Вирішення таких завдань дає принцип максимуму - математичний метод, розроблений Понтрягиним і його учнями.
Поведінка математичної моделі ОУ описується звичайним диференціальним рівнянням, у векторній формі, яке має вигляд:
|
(4.1) |
або в скалярній формі
|
(4.2) |
,
де
-
вектор стану,
-
вектор управління,
t – час ,
-
інтервал
часу функціонування системи,
;
n
-
мірний евклідово
простір, елементами служать вектори;
;
-
безліч
допустимих значень управління;
-
безперервна
разом зі своїми приватними похідними
векторна функція.
Момент
початку процесу
заданий,
а момент закінчення процесу
визначається
першим моментом досягнення крапкою (x,
t)
якійсь
заданій гіперповерхні
,
тобто
в момент
.
Початкова
умова
задає
початковий стан процесу в просторі
.
Передбачається, що при управлінні використовується інформація тільки про поточний час, тобто система управління є розімкненою і має програмне управління.
Малюнок 4.1 - Структурна схема процесу управління
Безліч допустимих управлінь утворює кусочно-безперервні функції u(t) із значеннями в області .