3.2. Обчислення коефіцієнтів лінійної регресії b1 і b0

Коефіцієнти парної лінійної регресії визначаються за допомогою наступних формул:

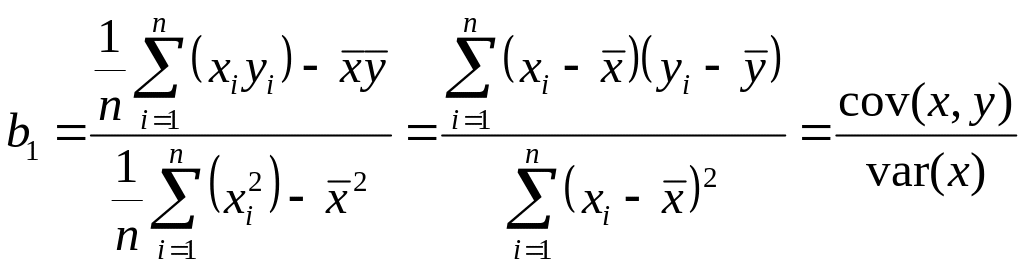(1)

(2)

1. Обчисліть значення коваріації між залежною та незалежною змінними та дисперсію незалежної змінної, використовуючи для цього функції КОВАР та ДИСПР, та за допомогою формули (1) і отриманих результатів обчисліть значення коефіцієнта b₁.

2. Використовуючи функцію СРЗНАЧ, обчисліть середні значення залежної змінної y та незалежної змінної x, та за допомогою формули (2) і отриманих середніх значень обчисліть значення оцінки b₀ моделі парної лінійної регресії.

3.3. Побудова лінії регресії на діаграмі.

1. Запишіть функціональний вираз отриманої лінії регресії. Та за отриманим функціональним виразом відшукати умовні середні значення залежної змінної ŷ_і за умови, що незалежна змінна х прийняла значення х_і, тобто обчислити множину значень ŷ_і = =М(y|x=x_i)=b₀+b₁x_i.

2. Поряд з діаграмою розкидання координат точок (y_i, x_i) побудуйте діаграму розкидання точок (ŷ_i, x_i), використовуючи для цього вже побудований шаблон діаграми (дивись розділ 3.1 даної інструкції).

3.4. Використання функції линейн для визначення статистик економетричної моделі

Оцінки параметрів b_i багатофакторної або парної лінійної регресії, а також переважну більшість статистик для оцінки якості (адекватності) моделі в Microsoft Excel можна отримати за допомогою стандартної функції ЛИНЕЙН( ), яка відноситься до категорії статистичних функцій. Аргументи даної функції є:

1. Вектор залежної змінної Y, що має назву «Известные_значения_y» (у Excel - це стовпець або рядок значень залежної змінної, причому, якщо вектор незалежної смінної в таблиці Excel заданий як стовпець, то і незележні змінні необхідно заносити у таблицю стовпцями, а якщо вектор залежної змінної Y у таблиці Excel заданий як рядок, то і незележні змінні необхідно заносити у таблицю рядками);

2. Матриця (усі стовпці) множини незалежних змінних X, що має назву «Известные_значения_x» (у Excel - це стовпець або рядок значень залежної змінної, причому, якщо вектор незалежної смінної в таблиці Excel заданий як стовпець, то і незележні змінні необхідно заносити у таблицю стовпцями, а якщо вектор залежної змінної Y у таблиці Excel заданий як рядок, то і незележні змінні необхідно заносити у таблицю рядками);

3. Логічна змінна, що має назву «Конст» та вказує: чи потрібно визначати вільний член b₀ лінійної регресії, чи ні. Якщо у якості цієї змінної занести число 1 або слово ИСТИНА (або TRUE), то функція ЛИНЕЙН буде обчислювати та відображати коефіцієнт b₀ та всі інші статистики з урахуванням наявності коефіцієнту b₀, а якщо 0 або слово ЛОЖЬ (або FALSE) – то ні.

4. Логічна змінна, що має назву «Статистика» та вказує: чи потрібно крім значень коефіцієнтів b_i відображати статистики для оцінки якості моделі. Якщо у якості цієї змінної занести число 1 або слово ИСТИНА (або TRUE), то функція ЛИНЕЙН буде обчислювати та відображати вказані статистики, а якщо 0 або слово ЛОЖЬ (або FALSE) – то ні.

Примітки:

1. Функція ЛИНЕЙН( ) обчислює статистики для ряду з використанням методу найменших квадратів, щоб обчислити пряму лінію, яка найкращим чином апроксимує наявні дані. Функція повертає масив, який визначає отриману пряму та основні статистичні характеристики, що можуть бути використані для визначення адекватності побудованої регресійної моделі. Оскільки повертається масив значень, функція повинна задаватись у виді формули масиву.

2. Функція у виді формули масиву вводиться наступним чином. Спочатку у визначену для цього комірку вводиться функція. Потім за допомогою маркера виділяється область, яка має п’ять рядків, а кількість стовпчиків виділеної області дорівнює кількості коефіцієнтів у регресії, що підлягають визначенню. Потім натискають клавішу F2 та відпускають її, а потім  клавіші CTRL+SHIFT+ENTER.

Функція ЛИНЕЙН обчислює та виводить у виділені комірки наступні статистики:

• коефіцієнти лінійної регресії, розташовані у першому рядку у зворотному порядку;

• стандартні (середні квадратичні) відхилення 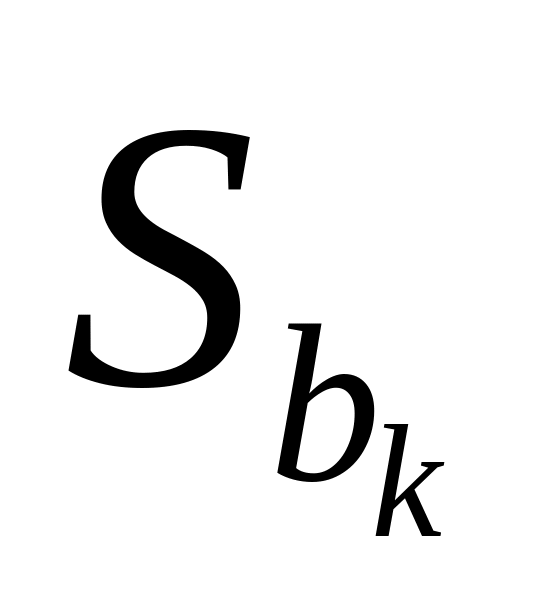для обчислених коефіцієнтів регресії, розташовані у другому рядку під відповідними коефіцієнтами регресії ;

• коефіцієнт детермінації – у першому стовпчику третього рядка;

• стандартну похибку оцінки y (корінь квадратний з MSE) - у другому стовпчику третього рядка;

• F-статистику Фішера - у першому стовпчику четвертого рядка;

• кількість степенів вільності суми квадратів залишків - у другому стовпчику четвертого рядка;

• суму квадратів регресії - у першому стовпчику п’ятого рядка;

• суму квадратів залишків - у другому стовпчику п’ятого рядка.