1-4 Понятие оптимизации. Основные задачи оптимизации в электроэнергетике. Степени свободы электроэнергетической системы. Допустимый и оптимальный режимы.

птимальным режимом работы - режим в соответствии с некоторым критерием оптимальности.

Оптимизация – задача решение которой выявляется оптимальный режим.

Критерий оптимальности:

- количественный (снижение расхода условного топлива на ТЭС);

- качественный (улучшение влияния электроэнергетического объекта на экологию).

Задачи оптимизации в электроэнергетике:

1. Стратегия развития энергосистемы;

2. Выбор оптимальной конфигурации эл.сетей, соединяющих подсистемы или распределяющих передающих энергию внутри сети;

3. Оптимальное распределение нагрузки между электростанциями;

4. Оптимальная стратегия использования материальных ресурсов;

5. Выбор оптимальных маршрутов грузоперевозки, в т.ч. перевозки топлива;

6.Выбор точек размыкания линии с двухсторонним питанием;

7. Выбор маршрута осмотра электротехнических объектов.

Взаимосвязь расчета установившегося режима и его оптимизации.

Параметры уравнения установившегося режима :

- - независимые, заданные параметры;

- - зависимые параметры.

Уравнения установившегося режима связывают между собой его параметры.

Пусть k – число уравнений, n – число неизвестных. Если k=n, то система полностью определена. При k<n система недоопределена. Избыток числа неизвестных над числом уравнений физически означает что система имеет (n-k) степеней свободы.

УУР БМ

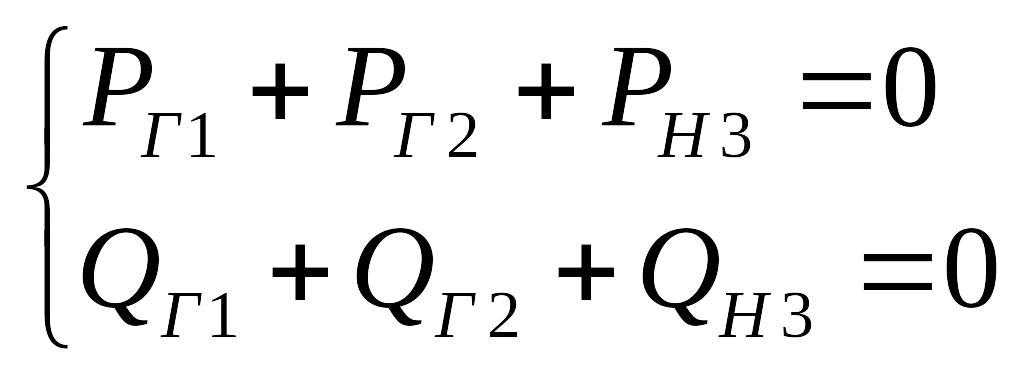
- заданы

Система имеет 2 степени свободы 2 любых параметра могут быть заданы в пределах минимальных и максимальных допустимых значений.

Регулируются P и Q:

- с помощью регулирующих трансформаторов;

- при включении/отключении оборудования.

Из всех возможных состояний системы наибольший интерес представляют допустимые режимы, в которых значения параметров установившегося режима находятся в заданных пределах.

Задача оптимизации: найти наиболее экономичный режим.

Рост числа степеней свободы – рост возможности оптимизации и усложнение задач.

		генератор	нагрузка
Z	X	Q,	U,
	Y	P,U	P,Q

В задаче оптимизации используются добавочные степени свободы для изменения переменных параметров режима, чтобы из множества состояний системы выбрать такое, которое обеспечит минимальный суммарный расход условного топлива, что снижает экономические затраты.

При оптимизации режима за счет наличия степеней свободы выбираются параметры режима, обеспечивающие минимальные суммарные потери активной мощности.

5-7 Применение метода множителей Лагранжа при решении задач оптимизации в электроэнергетике.

Определение оптимального распределения нагрузки между ТЭС методом множителей Лагранжа. Относительный прирост топлива.

Метод позволяет отыскать условные или относительные экстремумы функции, которые являются ее минимумом или максимумом при выполнении дополнительных условий в форме равенств, т.е. уравнений связи.

Данный метод дает возможность найти систему уравнений, которой удовлетворял экстремум функции на множестве N. Для того чтобы найти экстремум, характеризующийся на множестве N вектором необходимо найти m чисел , которые совместно с вектором удовлетворяют уравнениям с неизвестными.

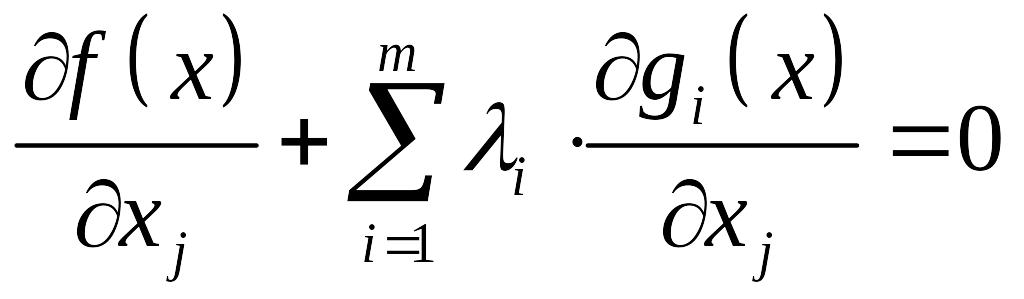
Эти уравнения получены как условный экстремум функции Лагранжа.

Например, найти Р.

Заданы расходные характеристики

- целевая функция

Уравнения ограничения

Уравнения связи – расходные характеристики

Функция Лагранжа

Условие оптимальности распределения нагрузки:

8-9Наивыгоднейшее распределение нагрузки между ТЭС без учета потерь активной мощности. Физический смысл равенства относительных приростов.

Это случай задачи наивыгоднейшего распределения нагрузки между агрегатами электростанций или в ЭС с высокой концентрацией мощности.

-усл-ие оптимальности, т.е. оно соотв-ет рав-ву отн-ых приростов

Рассмотрим на примере из 2-х агрегатов Эл/ст

Условие оптимальности – затраты топлива на единицу мощности в месте её потребление равны на Эл. Станциях. На практике b_i не удовлетворяют этому условию и подлежат корректировке по методике.

10-11Определение оптимального распределение нагрузки в энергосистеме с ГЭС и ТЭС методом множителей Лагранжа. Относительные приросты ТЭС и ГЭС.

З-ча наив-шего распределения нагр-и в гидротепл. Системе делится на:

1 З-ча оптим-ции длит-ных реж-ов; 2 З-ча оптим-ции краткосрочн. режим (сутки и менее).

Для всего цикла регул- ия ГЭС находит наив-шее распр-е нагрузки м/у всеми станциями сист-ы, и опр-ет оптим режим исп-ния гидроресурсов, т.е. график сработки и заполнения водохранилищадля всей ГЭС с-мы. На основании этих расчётов регламентируются гидроресурсы на более короткий период оптим-ции.

Метод множителей Лагранжа

1 Ур-ние цели

- расход топлива эквив-ой ТЭС за период времени Т

2 Ур-ние связи

2.1 - расх-ая хар-ка ТЭС

2.2 - расх хар-ка ГЭС

3 Ур-ние огр-ний

-ур-ний:

- сумма нагр-ки, - сумма потерь.

ур-ние:

- заданные огр-ния по стоку для j-ой ГЭС, - расход, с которым работала ГЭС в период Т

- мощн-ти -ой ГЭС на инт t

4 Ф-ция Лагранжа

Кол-во неиз-ых

ур-ний: ; ….

, где ,

ур-ний: (*)

Все величины, вход-щие в сист-у ур-ний (*) опр-ся энерг-ми хар-ми оборуд-ния, т.е. отн-ный прирост расх топлива (В) и расх топлива на ТЭС (q), или же парам-ми сети.

Индексы при этих велич-ах можно опус-ть

- усл оптим-ции режима гидро-теплов с-мы.

Смысл усл-ия оптим-ции

В том, что для наив-шего распр-ия нагрузки необх-мо в теч всего периода оптим-ции собл-ть пост-ное соотн-ние м/у ТЭС и каж-ой из ГЭС, т.е. м/у ТЭС и -ГЭС нагрузка должна рапр-ся по соотн-ию

и это постоянное соотн-ие должно собл-ся в теч. всех периодов оптим-ции

Соотн-ие м/у ТЭС и -ГЭС

При усл-вии соблюдения баланса величины , связывают м/у собой режимы ТЭС и соотв-щей ГЭС.

12 Размерность и физический смысл множителей Лагранжа в задачах оптимизации распределения нагрузки в энергосистеме.

Размерность и физический смысл множителей Лагранжа

1 ТЭС и 1 ГЭС

если пренебречь потерями , то усл-вие оптим-ции

;

- мера эффект-ти использ-я гидроресурсов, т.е. ккая экономия топлива будет получена на ТЭС при измен-ии расхода на ГЭС на .

Наивыгодн-ший режим тот, при к-ом эфф-сть исп-ния ресурсов на к-ой ГЭС одинакова на всём периде оптим-ции, т.е.

; ;

;

,

Эффект-ть использ-я гидроресурсов в данной с-ме (т.е. в с-ме с недозагруженной ГЭС) пропорц-на расходу на ГЭС.

Если ГЭС работает с малым расходом, то в с-ме имеется неэкон-но работающая ТЭС.

13. Оптимальное распределение нагрузки при постоянном напоре гэс и структурная схема алгоритма поиска данного распределения.

Для наивыгоднейшего распределения нагрузки необходимо по методу Лагранжа в процессе расчёта подобрать  в соответствии с заданным стоком ГЭС и найти такое распределение нагрузки, при котором t = const для всего периода оптимизации

Дано:

1) Р₁, Р₂ ..Р_К t₁ …t_К – нагрузки

2) Расходные характеристики В(Р_ТЭС ), Q(P_ТЭС )

3) Характеристики относительных приростов q(P_ГЭС ), b(P_ТЭС)

4) Ограничение по стоку и по мощностям станций W задано ГЭС

Р_ТЭС max; Р_ТЭС min; Р_ГЭС max; Р_ГЭС min.

2- Задаются мощности ГЭС для каждого интервала, и проверяется его допустимость -3. Если условия не выполняется мощность, корректируется мощностью -4 определяем мощность ТЭС из условия баланса мощностей проверяем ограничения – 5. Определяем суммарное прирост потерь для каждой Эл ст и определяем суммарные приросты для всех интервалов 7,8

Определяем для каждого интервала – 9 среднее и отклонение. В зависимости от знака 12 корректируются мощности (2).

14.Оптимальное распределение нагрузки при переменном напоре гэс.

Изменение напора приводит к колебаниям уровней верхнего и нижнего бьефов.

ЭЭС: 1ТЭС и 1ГЭС → произвольное распределение графика нагрузки

; ;

- экономия топлива на ТЭС;

;

; ; ;

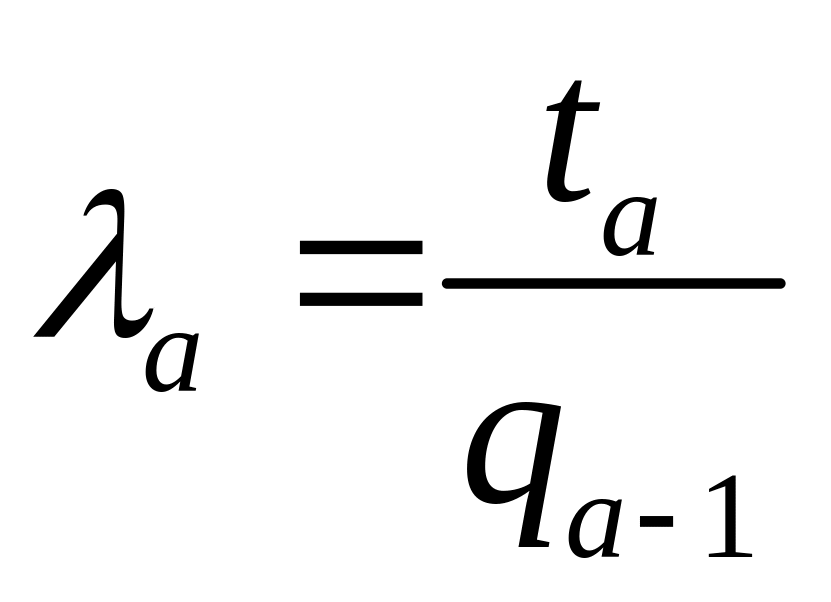- дополнительный расход топлива из-за ↓Q.

; ;

;

ta : дополнительный расход топлива, вызванный повышением уровня нижнего бьефа.

;

В момент tБ :

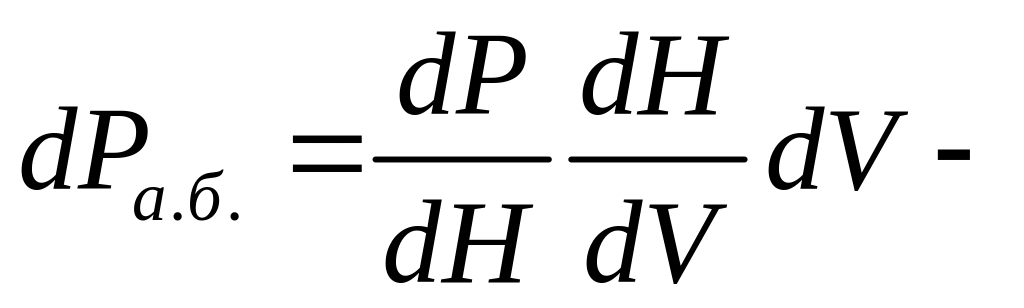изменение мощности из-за изменения

;

Общее изменение расхода топлива:

экономия топлива из-за ↑Q в tA;

дополнительный расход топлива из-за ↓Q в tБ;

дополнительный расход топлива из-за ↑ в tA;

экономия топлива из-за ↓ в tБ;

дополнительный расход топлива из-за ↓ в tA… tБ;

Если режим I лучше режима II →

→ режим II экономичнее режима I

- условие равноэкономичности режимов

15-16.Оптимальное распределение нагрузки между агрегатами эл/ст.

Использование метода множителей Лагранжа позволяет получить условие наивыгоднейшего распределения нагрузки между агрегатами эл/ст. в виде равенств отношений приростов расхода первичного ресурса (приведенной мощности) к приращению вторичного ресурса (полезной мощности) при соблюдении балансовых ограничений. 1)М/у агрегатами ТЭС:

а) м/у турбинами: b_T,i= ∆D_i/∆P_i= idem

б) м/у котлами: b_K,i= ∆B_i/∆D_i= idem

в) м/у блоками: b_Б,i= ∆B_i/∆Р_i= idem

где ∆D_i – прирост расхода пара; ∆P_i – прирост расхода мощности турбин; ∆B_i – прирост расхода топлива; b_T,I – относительный прирост турбины; b_k,I - относительный прирост котлов; b_Б,I – относительный прирост блока (блок=котел+турбина)

Н а эти уравнения накладываются ограничения, т.к. характеристики имеют скачки и участки постоянного прироста.

b_T1 b_T2

_min P_{1 max} P _min P_{2 max} P

Р₁>P₂

P_min1, P_max1 – минимальная и максимальная мощность турбины 1

P_min2, P_max2 – минимальная и максимальная мощность турбины 2

P_min=P_min1+P_min2

1. Если P_min<P<P_min+P₂ – загрузка турбины 2

2. P_min+P₂<P<P₁+P₂ – загрузка агр.1

3. P₁+P₂<P<P₁+P_max2 – загрузка агр.2

4. P>P₁+P_max2 – загрузка агр.1

При такой методике всегда используется агрегат с наибольшей экономией топлива. Оптимальным является последовательность включения агрегатов ЭС в порядке возрастания их относительных приростов.

2) Распределение нагрузки м/у агрегатами ГЭС

Распределение нагрузки м/у агрегатами ГЭС является наивыгоднейшим, если они работают с одинаковыми относительными приростами.

Задача наивыгоднейшего распределения нагрузки м/у агрегатами станций проста, если известны характеристики относительных приростов. Но в условиях эксплуатации желательно использовать не характеристики, а измерение относительных приростов. Для этого с малым шагом дискретности измеряем а₁ и а₂ и соответствующие им Р₁ и Р₂.