III. Порядок выполнения лабораторной работы

1. С помощью программы NAIMKVA.BAS, задавшись степенью регрессионного полинома, ввести исходные данные в ЭВМ.

2. По результатам вычислений сравнить полученную среднеквадратичную ошибку с заданной. Если d расчетное больше чем d заданное, то повторить пункт 1, увеличив степень полинома на 1.

3. Ввести значение помехи и, повторив расчеты, оценить ее влияние на изменение величины ошибки.

IV. Содержание отчета

Распечатки результатов вычислений, оценка влияния помехи на точность аппроксимации и выводы по работе.

Литература: [1];[3].

Работа 7 Построение регрессионной модели объекта по данным активного и пассивного экспериментов

I.Цель работы. Овладение методами идентификации объектов управления по данным активного и пассивного экспериментов.

II. Основные теоретические положения

Разработанная программа предназначена для исследования технологических процессов непрерывного типа Моделируемый технологический процесс описан в программном модуле в нескольких вариантах.

Структурная схема исследуемого технологического процесса:

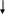e₁

x₁ у₁

x₂ e₂ y₂

. . . . . .

x_p e_k y_po

y_1,y₂,......,y_pо– выходные величины , определяющие качество выпускаемой продукции ;

х₁,х₂,...,х_p - управляющие воздействия, с помощью которых осуществляется управление технологическим процессом;

е₁,е₂,...,е_k - случайные возмущения (помехи), связанные с действием полученных факторов.

Все методы идентификации разделяются на активные и пассивные. К первым относятся методы, основанные на использовании информации, полученной при проведении активного эксперимента, когда на вход объекта искусственно подаются воздействия той или иной формы, которые вызывают соответствующие изменения его выходов. Вторые используют информацию, полученную при пассивном наблюдении за объектом в процессе его нормальной эксплуатации.

Активные методы идентификации требуют специальной аппаратуры и устройств для создания различных по физической природе типовых воздействий, но зато позволяют быстрее и с большей достоверностью получить требуемую математическую модель объекта. В условиях реальных технологических процессов не всегда удается провести активный эксперимент. В этих случаях исследователь вынужден только регистрировать естественные изменения переменных.

При идентификации статических параметров объекта широко используется аппарат регрессивного анализа. Этот аппарат позволяет получить математическую модель объекта в форме уравнения регрессии, т.е. в виде алгебраического полинома, определяющего статистическую связь между выходными и входными переменными объекта. При этом вид и порядок уравнения регрессии предполагаются уже известными исходя из анализа априорной информации, а определению подлежат лишь численные значения его коэффициентов, т.е. по существу ставится задача параметрической идентификации. Регрессионный анализ особенно удобен в сочетании с методом наименьших квадратов, который обеспечивает вычисление коэффициентов регрессионной модели из условия минимума среднеквадратичной погрешности.

.