7.3. Алгоритмы оптимальной стабилизации

Основное назначение данных алгоритмов заключается в поддер­жании оптимального равновесного состояния объекта в условиях постоянно действующих возмущений. В АСУТП эти алгоритмы использу­ются в основном на уровне локального управления, причём их целе­сообразно применять только в тех случаях, когда известные типовые законы управления (П, ПИ, ПИД) не обеспечивают заданного качества управления локальным объектом.

Синтез оптимальных алгоритмов стабилизации, осуществляемый на основе АКОР, в математической постановке формулируется следую­щим образом.

Задан объект оптимизации, уравнения состояния которого имеют вид:

= AX + BU; Y = CX (7.3.1)

и краевые условия:

X(0) = X₀; Y(0) = Y₀; X( ) = Y( ) = 0.

Необходимо синтезировать оптимальное управление U⁰(X), при котором квадратичный функционал:

(7.3.2)

минимален.

В результате решения данной задачи (подробнее она рассмотре­на в курсе "Основы теории оптимизации") формируется оптимальное управление U⁰(X), обеспечивающее малые отклонения координат век­тора состояния X и выходных переменных Y.

Однако синтезированный с помощью АКОР регулятор является оптимальным лишь при изменении начального состояния системы. Та­кие случаи встречаются, например, при проектировании автопилотов или систем наведения на неподвижные цели, когда в процессе дви­жения система уже не подвергается другим воздействиям, кроме управ­ляющих.

Однако в условиях АСУТП система стабилизации постоянно находится под действием возмущений, характер изменения которых чаще всего является случайным. Для таких систем величина критерия оптимальности (7.3.2) будет зависеть не только от вектора управле­ния U, но и от вектора возмущений Z, поскольку последний также влияет на траекторию движения системы:

I = I(Y; U; Z). (7.3.3)

При оптимизации систем с возмущениями возможны два подхода [3]: компенсационный (он осуществляет приведение исходной сис­темы к системе без возмущений) и прямой (он связан с непосредст­венной минимизацией критерия с учётом фактических возмущений).

Компенсационный метод сводится к нахождению составляющей управления U_Z, компенсирующей возмущения, и после­дующему определению оптимального управления U₀, минимизирующего критерий без возмущения вида (7.3.2). В этом случае суммарное управ­ление

U = U_Z + U₀.

Однако полная компенсация возмущения возможна только в том случае, когда могут быть соблюдены условия абсолютной инвариантности. Выполнить это на практике часто не удаётся из-за ограниче­ний на управление и трудностей получения идеальных производных; кроме того, затраты на управление в ТП часто очень велики, поэто­му полная компенсация не всегда целесообразна. Следовательно, ком­пенсационный метод имеет ограниченное применение.

При использовании прямого метода оптимальное управ­ление формируется по прогнозу о возмущениях и текущем состоянии объекта. В этом случае исходная минимизация функционала (7.3.3) за­меняется последовательностью минимизаций функционалов на скользя­щем интервале времени (последовательностью укороченных задач):

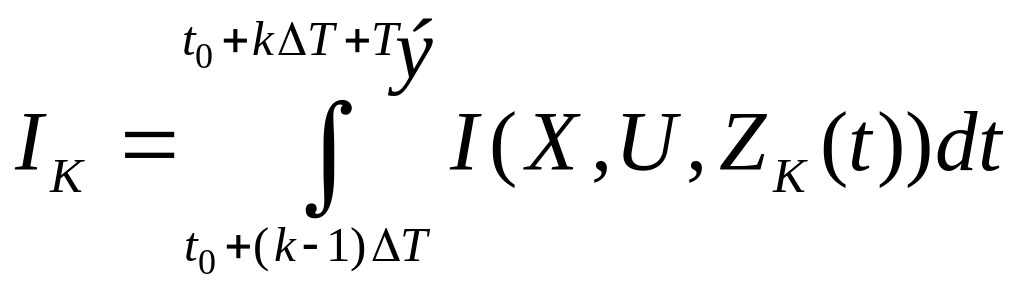, (7.3.4)

где T_Э - интервал экстраполяции (прогноза) возмущённого дви­жения системы;

∆Т - интервал коррекции (ΔТ << Т_Э);

Z_K(t) - прогнозируемое на k-м интервале возмущение;

T_оп – t₀ - текущий интервал оптимизации;

k = 1, 2, … , .

По результатам синтеза на каждом k-м интервале получаем последовательность управлений:

U_K(t) = U(t), t є (t₀ + (k – 1)ΔT; t₀ + kΔT + T_Э),

из которой на объекте реализуется лишь последовательность началь­ных участков:

U(kΔT) = U(t), t є (t₀ + (k – 1)ΔT; t₀ + kΔt).

Такой подход к решению оптимизационной задачи назван в [3] методом упреждающей коррекции. Отметим его некоторые особенности.

1. Метод является декомпозиционным, поскольку объём укорочен­ной задачи значительно меньше объёма исходной. С увеличением вре­мени прогноза укороченная задача приближается к исходной и при T_Э = T_оп – t₀ задачи адекватны. Однако при этом ухудшается точность прогноза, а следовательно, и качество управления. При Т_Э → 0 уп­равление становится слишком «близоруким», т.е. прогноз отсутствует.

2. Метод является адаптивным, поскольку предполагает непре­рывное пополнение и периодическую коррекцию информации о возмущениях.

3. Если управления исходной и укороченных задач совпадают хотя бы на интервалах (t₀ + (k – 1)ΔT; t₀ + kΔT), то реализуемое управление оптимально.

Чтобы последовательность U(k∆T) могла быть найдена оператив­но, в такт с движением системы, необходимо найти решение укорочен­ной задачи за время Т_р ≤ ΔТ. Это осуществляется по быстрой модели системы, на которой в увеличенном по сравнению с натуральным масш­табе времени определяется управление, минимизирующее функционал I_K. Системы с быстрой моделью относятся к классу двушкальных систем, т.е. они имеют две шкалы времени, функцию управления в них выполняет "быстрая" часть. В её состав входят модели объекта и управляющего устройства, которые работают в режиме периодичес­кого решения задачи управления в увеличенном масштабе времени. Найденный с учётом будущего поведения объекта закон оптимального управления передаётся в блок вывода данных для реализации на объек­те.

Модель объекта формируется на основе априорной информации и периодически подстраивается к изменяющимся условиям.