2.2. Технологические процессы как объекты управления

Современный технологический процесс (ТП) представляет собой сложный многомерный объект управления, включающий ряд локальных автоматических систем. Состояние такого объекта в статическом режиме характеризуется векторами выходных координат Y, возмущающих Z и управляющих воздействием U (рис. 2.2.1).

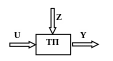
Рис. 2.2.1. Технологический процесс как объект управления

Компонентами вектора Y являются выходные параметры ТП (объём выпуска и показатели качества продукции, различные затраты на всех участках технологического процесса и т.д.).

Вектор возмущающих воздействий Z определяется количественными и качественными характеристиками исходного сырья, отклонениями нерегулируемых координат процесса и т.д. Составляющие вектора U связаны с параметрами, определяющими выбор технологических режимов процесса и распределение материальных и энергетических потоков между агрегатами.

Для процесса на рис.2.2.1 связь между входными и выходными переменными устанавливается с помощью выражения:

Y=A(U,Z),

где конкретное выражение оператора A зависит от выбранной модели ТП. Это может быть система линейных или нелинейных алгебраических уравнений, система обыкновенных дифференциальных уравнений, уравнения условных плотностей или функции распределения и т.д. В зависимости от способов представления оператора и входных и выходных переменных обычно и производится классификация процессов. Входные и выходные переменные могут рассматриваться как детерминированные или случайные.

Модель процесса называется детерминированной, если ее оператор детерминирован.

Модель процесса называется стохастической, если соответствующий ей оператор является случайным.

Сложный ТП представляется в виде последовательности (цепочек) технологических операций.

ТП как последовательность операций может быть представлен следующими способами:

• линейное представление (предполагается наличие первой и последней операции) это последовательная цепочка операций.

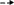
• сложное линейное представление – последовательная цепочка с параллельными ветвями

• циклическое представление

Обычно рассматриваются два вида цепочек: 

• выходные переменные на i-й операции зависят от входных переменных на этой же операции и не зависят от входных переменных на операциях с номерами <i;

• входные переменные на всех или некоторых операциях влияют на выходную переменную последней операции в цепочке.

2.3. Управление производством однородной продукции (непрерывные процессы)

Технологические процессы непрерывного производства однородной продукции имеют ряд особенностей, позволяющих выделить их в особый класс объектов управления. Это, прежде всего, большая мощность и высокая производительность, значительная стоимость строительства и длительные сроки эксплуатации. С позиций управления, объекты, производящие однородную продукцию, часто являются нестационарными и стохастическими. При построении систем управления ТП, в основном, определяются динамическими свойствами процесса и режимами его работы. Если интервал времени между двумя последовательными возмущениями много больше длительности переходного процесса в объекте, то принято считать, что такой технологический процесс работает в статическом режиме. Если эти времена соизмеримы, то основным является динамический режим работы процесса.

При оптимизации статического режима работы ТП целесообразно ис­пользовать схему, представленную на рис.2.3.1, где

ОУ - объект управления;

- вектор управляющих воздействий;

- вектор контролируемых возмущений;

- вектор неконтролируемых возмущений;

- вектор выходных переменных объекта;

КО - критерий оптимальности, определяющий целевую функцию J(Y).

F

Z

ОУ

КО

U

Y

J(Y)

Рис.2.3.1. Оптимизация статического режима работы ТП

В задачах статической оптимизации чаще всего в качестве КО используются либо технологические критерии (например, максимальный объём продукции с единицы объёма аппарата), либо один из экономи­ческих критериев (производительность, объём капитальных вложений, коэффициент полезного действия, себестоимость продукции и т.п.). При известном КО качество функционирования ТП определяется значе­нием целевой функции J(•). В зависимости от априорных сведений об объекте и условиях внешней среды (характера возмущающих воздействий и возможностях их измерения) задача статической оптимизации для рассматриваемой схемы может решаться разными способами.

Если процесс плохо определён (априорные сведения отсутствуют), то задача оптимизации решается путём организации поиска на самом процессе (рис.2.3.2). В этом случае в качестве модели объекта высту­пает сам процесс, на который подаются расчётные значения вектора управления U. На основе возникающей реакции объекта J(Y) режим оптимизируемого процесса последовательно улучшается.

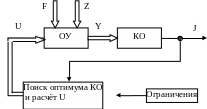
Рис. 2.3.2. Оптимизация статического режима ТП без модели

При таком способе решения задачи оптимизация осуществляется с помощью итерационной процедуры, в которой переменные параметры управления корректируются таким образом, чтобы в итоге был достиг­нут оптимум КО (целевой функции J(Y)).

Процедура состоит из четырёх этапов:

• на первом этапе с учё­том ограничений вычисляются изменения переменных параметров управ­ления, приближающих целевую функцию к оптимуму,

• на втором этапе выполняется корректировка переменных управления,

• на третьем - ана­лизируются результаты предыдущего шага,

• на четвёртом - определя­ется, достигнут ли оптимум целевой функции. Если она ещё не при­няла оптимального значения, процедура повторяется.

Данный метод используется, когда составление модели невозможно по техническим причинам или невыгодно из экономических соображений, если модель не приспособлена для внесения в неё различных усовершенствований, или неточна (ненадёжна) при предполагаемых условиях работы.

Однако применение оптимального управления ТП, использующе­го поиск на самом объекте, в настоящее время ограничено, так как многие ТП по условиям эксплуатации часто не допускают подачи на их вход какого-либо пробного сигнала из-за возможности воз­никновения нежелательных технологических условий и аварийных состояний. Кроме того, при значительной инерционности объекта и большом числе управляющих воздействий время поиска оказывается недопустимо большим.

В связи с этим статическая оптимизация технологических процессов чаще всего осуществляется с помощью моделей объектов.

При оптимизации с использованием математической модели мо­гут быть применены технические структуры двух основных видов.

1. Системы управления, работающие по разомкнутому циклу (по возмущению). Такие системы реализуются на специализированных вычислительных устройствах, определяющих оптимальные значения управляющих пере­менных при изменяющихся внешних условиях. Эти системы удобны с точки зрения простоты конструкции, надёжности и работоспособности. Они широко используются для управления стационарными технологичес­кими процессами при наличии их адекватны моделей и отсутствии не­контролируемых возмущений,

F = 0 (рис.2.3.3.).

Как показано на рисунке, поиск оптимального управления в этом случае осуществляется по модели объекта, а на сам объект по­даются только оптимальные значения координат управления (U)_опт.

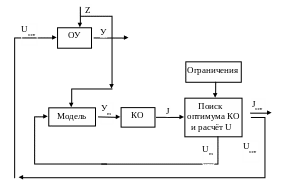
Рис. 2.3.3. Система управления ТП по разомкнутому циклу

2. Системы управления с контуром адаптации, действующим по принципу обратной связи. Основное назначение контура адаптации в этих системах состоит в слежении за параметрами объекта, изменяю­щимися вследствие его нестационарности или действия неконтролируе­мых возмущений. Поэтому подобные контуры адаптации часто называют идентификаторами.

Адаптивная система с идентификатором (рис.2.3.4) постоянно уточ­няет модель объекта, по которой осуществляется оптимизация, делая всю систему в целом нечувствительной к изменениям нестационарного технологического процесса.

Критерием адекватности математической модели процессу служит сигнал рассогласования

ΔJ = J - J_M. (2.3.1)

При ΔJ = 0 модель адекватна процессу и коэффициенты модели не меняются.

При ΔJ ≠ 0 идентификатор, используя полученный сигнал рассогласования, уточняет коэффициенты модели до тех пор, пока ΔJ не станет равно нулю.

Jм

Рис. 2.3.4. Система управления ТП с контуром адаптации

Адаптивные системы с идентификатором используются для ста­тической оптимизации нестационарных и даже стационарных ТП при наличии у последних значительных неконтролируемых возмущений.