
- •3. Математичне моделювання в імунології
- •3.1. Основні компоненти імунної відповіді
- •3.2. Форми інфекційного захворювання
- •3.3. Проста модель інфекційного захворювання
- •3.4. Існування та невід’ємність розв’язку
- •3.5. Стаціонарні розв’язки
- •Розв’язавши систему, одержимо
- •3.6. Стійкість стану здорового організму
- •3.9. Вплив температурної реакції організму на динаміку захворювання
- •Список літератури
- •3.1. Основні компоненти імунної відповіді............................................. 57
3.9. Вплив температурної реакції організму на динаміку захворювання
Підвищення температури організму відбувається під впливом живих культур і вакцин, чужорідних білків та продуктів пошкодження і розпаду клітин та тканин. Пірогенна дія (підвищення температури) більшості бактерій пов’язана із звільненням при їх розпаді високомолекулярного комплексу – ендотоксину. Певною пірогенною дією володіють також продукти життєдіяльності бактерій.
Підвищення температури, з одного боку, спричиняє депресуючу дію на більшість бактерій і вірусів, на їх розмноження та проникнення у клітини організму. Що стосується вірусу грипу, то спричинена продуктами його розпаду пірогенна дія стимулює утворення в організмі інтерферону – захисного білка, що й пригнічує вірус. З іншого боку, підвищення температури в певних межах прямо пропорційно підвищує швидкість хімічних реакцій та активність ферментів, стимулює імунологічну активність, прискорює фізико-хімічні реакції імунітету.
Врахуємо
температуру організму
![]() у простій
моделі (3.7),
(3.8) інфек-ційного
захворювання
[1, 10].
у простій
моделі (3.7),
(3.8) інфек-ційного
захворювання
[1, 10].
Візьмемо до уваги гіпотезу, що швидкість розмноження антигенів зменшується із підвищенням температури таким чином:
![]() ,
(3.24)
,
(3.24)
де
0>0
– коефіцієнт розмноження при нормальній
температурі
![]() ,
1=
const>0.
Стимулювання
ростом температури синтезу білків,
зокрема імуноглобулінів,
опишемо лінійною залежністю
,
1=
const>0.
Стимулювання
ростом температури синтезу білків,
зокрема імуноглобулінів,
опишемо лінійною залежністю
![]() (3.25)
(3.25)
де 0
- коефіцієнт стимулювання імунної
системи при
![]() 1=const>0.
1=const>0.
При
побудові рівняння для
![]() використаємо
гіпотезу про
залежність
температури тіла від концентрації
FV-комплексів
[1].
Якщо концентрація FV-комплексів
менша деякого значення (FV)*,
то температура не підвищується. Якщо
FV(FV)*,
то температура підвищується. Тоді
рівняння для Q(t)
можна
записати у вигляді:
використаємо
гіпотезу про
залежність
температури тіла від концентрації
FV-комплексів
[1].
Якщо концентрація FV-комплексів
менша деякого значення (FV)*,
то температура не підвищується. Якщо
FV(FV)*,
то температура підвищується. Тоді
рівняння для Q(t)
можна
записати у вигляді:
![]() (3.26)
(3.26)
де
![]() коли
коли
![]() ,
і
,
і
![]() коли
коли
![]() .
.
Доданок із коефіцієнтом T компенсує підвищення температури. Клінічна практика дозволяє покласти T = 0.16. Врахувати, що температура при інфекційних захворюваннях не може перевищувати 400-40.50, дозволяє таке рівняння:
![]() ,
(3.27)
,
(3.27)
де 2 =const>0. У підсумку одержуємо математичну модель (3.8), в якій замість і використано відповідно () і () згідно з (3.24), (3.25).
Проведемо
короткий якісний аналіз моделі. Якщо
температурна реакція відсутня, то
концентрація антигенів
досягає
свого максимального значення
![]() у
точці t1,
коли
у
точці t1,
коли
![]() .
Коли температура росте, то
.
Коли температура росте, то
![]() ,
а
,
а
![]() .
Тому концентрація антигенів досягає
свого максимального значення
.
Тому концентрація антигенів досягає
свого максимального значення
![]() в
точці
в
точці
![]() ,
причому
,
причому
![]() (рис.3.13).
(рис.3.13).
Отже,
підвищення температури організму
зменшує максимальне значення концентрації
антигенів. Це веде до зниження
характеристики ураження органу-мішені
і може позитивно вплинути на перебіг
захворювання, особливо при гострих
формах захворювання із невизначеним
наслідком. Із рис.
1а
випливає, що при
![]() маємо хронічну форму захворювання, тоді
як ріст температури організму дає гостру
форму з одужанням.
маємо хронічну форму захворювання, тоді
як ріст температури організму дає гостру
форму з одужанням.
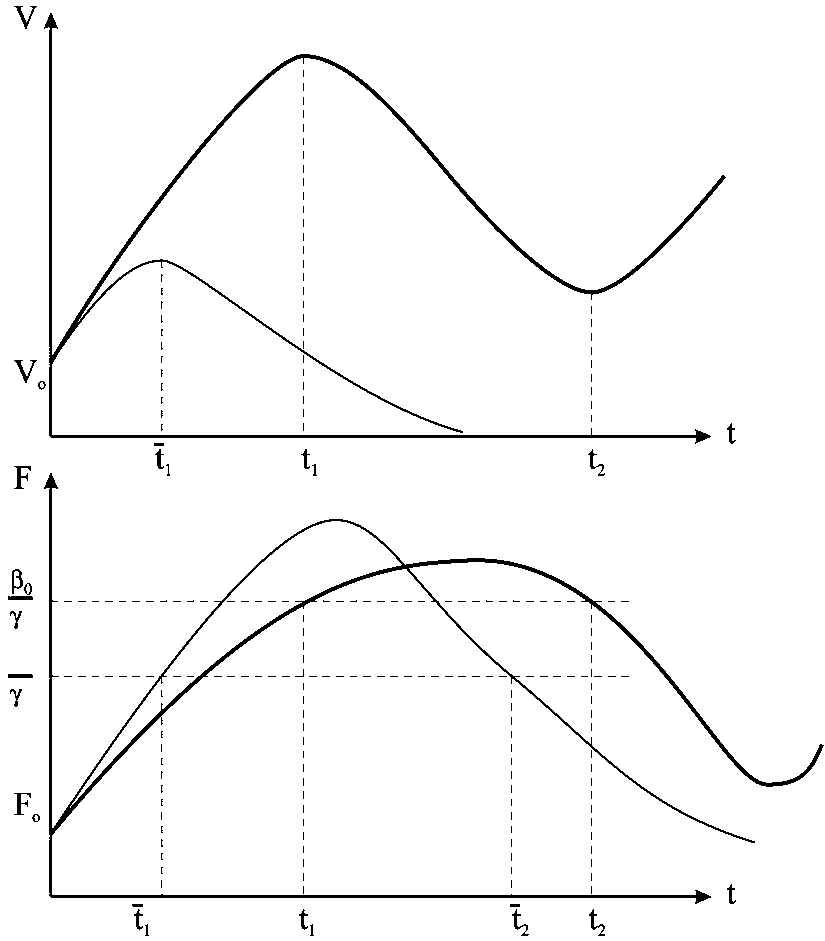
Рис. 3.13
Результати моделювання [10] вказують на важливість температурної реакції з погляду хронізації хвороби. Не викликане необхідністю пригнічення температурної реакції може сприяти переходу гострої форми захворювання в затяжну або хронічну. Крім того, деякі понижуючи температуру засоби мають аналогезуючу дію, зменшуючи вираженість клінічних симптомів, що може привести до недооцінки клінічної важкості захворювання й помилки у виборі тактики лікування.
Задачі
В монографії [8] запропонована така математична модель епідемії:
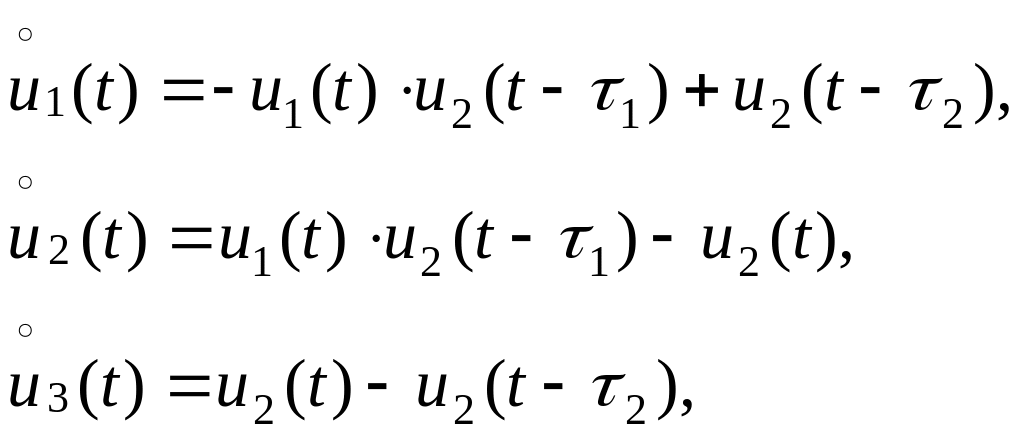
де
![]() - міра схильної до захворювання частини
населення;
- міра схильної до захворювання частини
населення;
![]() - частина інфікованого населення;
- частина інфікованого населення;
![]() - не схильна до інфекційного захворювання
частина населення.
- не схильна до інфекційного захворювання
частина населення.
1. Скласти
програму обчислення наближеного
розв’язку моделі на сітці з кроком
![]() Параметри моделі:
Параметри моделі:
![]()
![]() (діб);
(діб);
![]()
![]() при
при
![]()
![]()
![]()
2. Знайти стаціонарні розв’язки.
3. Порівняти одержані результати з результатами в [8].
4. Зробити висновки.
