3.5. Стаціонарні розв’язки

Для знаходження стаціонарних розв’язків врахуємо, що F_ = F = const, V_ = V = const і (m) = 1 (порогове значення m^*(0,1) ще не пройдено). Прирівнявши до нуля похідні в (3.1) – (3.4), одержимо систему рівнянь

( - F)V = 0,

VF – _c(C – C^*)=0, (3.12)

C – (_f + V)F = 0,

V – _mm = 0.

Один стаціонарний розв’язок

V₁= 0, C₁ = C^*, F₁ = C^* / _f , m₁ = 0 (3.13)

характеризує стан здорового організму. Віруси в організмі відсутні (V₁ = 0) і орган, проти якого він направлений, неуражений (m₁=0). Інший стаціонарний розв’язок

F₂ =  / , m₂ = V₂ / _m, (3.14)

а C₂ і F₂ знаходяться із системи лінійних рівнянь

V₂ - _c C₂ = - _c C^*;

 V₂ - C₂ = - (_f)/.

Розв’язавши систему, одержимо

V₂= , C₂= . (3.15)

Достатніми умовами існування такого розв’язку є виконання нерівностей:

V₂ > 0, .

Друга нерівність гарантує біологічно оправданий результат (m₂) = 1. Додатність розв’язку V₂>0 є наслідком виконання умов

>_c, _f> C^* (3.16₁)

або

<_c, _f< C^* . (3.16₂)

Зауважимо, що коли V₂ > 0, то C₂ > 0, оскільки C₂=( V₂+_f / ). Якщо _f= C^* і _c, то V₂ = 0, C₂=C^* і стаціонарні розв’язки (3.13) і (3.14), (3.15) збігаються.

Випадок =_c має наслідком існування сім’ї розв’язків, що біологічно необґрунтовано.

Розв’язок (3.14), (3.15) при виконанні умов (3.16) будемо тлумачити, як хронічну форму інфекційного захворювання.

3.6. Стійкість стану здорового організму

Розглянемо стаціонарний розв’язок (3.14) і запровадимо заміну

, , F = + F ^*, m = .

Для нових змінних одержимо систему рівнянь

,

, .

Лінеаризована система

, (3.17)

, .

Характеристичний многочлен для системи (3.17) набуває вигляду

або ( )(_с+)(_f +)(_m+)=0. Корені рівняння ₁=F^*, ₂=-_с<0, ₃= – _f <0, ₄= – _m<0.

За теоремою про стійкість за першим наближенням розв’язок (3.13) асимптотично стійкий, якщо ₁=F^*<0. Отже, доведена теорема.

Теорема 3.3. При малих збуреннях початкових умов достатньою умовою асимптотичної стійкості стаціонарного розв’язку (3.13), який відповідає стану здорового організму, є виконання нерівності

F^*<0. (3.18)

Наслідок. Якщо виконується умова (3.18), то величина запізнення не впливає на стійкість стану здорового організму. Справді, якщо в системі (3.18) покласти  = 0, то стаціонарний розв’язок і корені _і, і=1,…,4 залишаться без змін.

Уточненням результату теореми 1, яка має важливий біологічний зміст, є така теорема.

Теорема 3.4. [2, 3]. Якщо виконуються нерівності (3.11) і

0 < V₀ < V^*= , (3.19)

то концентрація антигенів спадає на інтервалі (0,+) і V(t)0, коли t. Причому, якщо 0 < V₀ < V^*, то для t > 0

0<V(t)<V⁰ exp(–at), а = C^*/(_f+V⁰) – >0.

Число V^* називається імунологічним бар’єром.

Наслідок [1, 2]. Якщо виконуються умови теореми 3.3 і

<_mm^*/V⁰, (3.20)

то і C(t)C^* , F(t) F^* , m(t) 0 для t.

Умова (3.20) забезпечує виконання нерівності m(t)<m^*. Дамо біологічну інтерпретацію результатів. Якщо здоровий організм володіє імунологічним бар’єром проти даного типу антигену і при інфікуванні антигенами він не пройдений, то незалежно від дози зараження і сили імунної відповіді хвороба не прогресує, а кількість антигену з часом прямує до нуля. Цей висновок вперше обґрунтований Г.І.Марчуком [7] .

Підвищення імунологічного бар’єру веде до неприйняття здоровим організмом інфекції і є одним із засобів профілактики хвороб. Підвищення імунологічного бар’єру можливе шляхом підвищення рівня імунокомпетентних клітин С^* у здоровому організмі, що в реальній ситуації може бути пов’язано із утворенням клітин пам’яті внаслідок перенесеної хвороби або вакцинації. Це випливає із нерівності (3.19) і того, що F^*=C^*/_f.

3.7. Стійкість хронічного процесу з малим ураженням органу. Після виконання заміни V= , C= , F= , m= в системі (1) для лінеаризованої системи одержимо характеристичне рівняння

W()= - (_m+)Z(),

де Z()=-³-a-²-b-+d+(g-f)e^-, a=_c+V₂+_f=C₂ / +_c>0,

b=_c(V₂+_f)- V₂, d=_c V₂>0, g= V₂>0, f=  V₂>0.

Теорема 3.5 [2, 3]. Достатніми умовами асимптотичної стійкості стаціонарного розв’язку (3.14), (3.15), який відповідає хронічній формі захворювання, такі:

1. _с1; (3.21)

2. < < .

Умови (3.21) можна трактувати так, що асимптотична стійкість розв’язку (3.14), (3.15) досягається при   , коли виконується перша з нерівностей (3.21) і

0 <  – F ^* <  0.33 (доба^-1).

Коефіцієнт  характеризує чутливість імунної системи, а

 – F ^* = < 0.33.

Тому ці умови біологічно можна пояснити таким чином [1]. По-перше, в організмі з високою чутливістю імунної системи може бути стійко присутньою популяція антигена з невеликою концентрацією. По-друге, антигени, що викликають стійкі хронічні форми захворювання в організмі з високою чутливістю ( >> 1), володіють в’ялою динамікою.

8. Можливі форми динаміки інфекційного захворювання та їх класифікація.

Проста модель інфекційного захворювання (3.8) дозволяє проаналізувати динаміку інфекційного захворювання. Найважливішим фактором у цьому процесі є концентрація антигена V(t) та його взаємодія з популяцією антитіл F(t).

Розглянемо дві межові форми. Нехай організм не виробляє антитіл даної специфіки, тобто F(t) = F⁰ = 0 для t  0 і  =  = 0. Тоді з першого рівняння (3.8) маємо

V(t) = V⁰e^t. (3.22)

Ураження органу-мішені описується у цьому випадку рівнянням

,

розв’язок якого з початковою умовою m(0) = 0 є

.

Якщо уражений орган не відновлюється (_m = 0), то

.

і для t_m = (1 +  / (V⁰)) /  орган-мішень уражається повністю. Така форма веде до летального наслідку і можлива, наприклад, для людей похилого віку, в яких імунна система відмовляє у вираженій реакції проти антигена, або у людей із набутим або вродженим імунним дефектом.

Інший межовий випадок характерний сильно вираженою імунною відповіддю, коли наявний запас антитіл в організмі достатній для нейтралізації популяції антигена. Нехай V₀ досить мале,  << , а F(t) = F*. Тоді

,

звідки V(t) = V0  0, коли t  , оскільки F^* -  > 0. Якщо антиген не розмножується ( = 0), то

V(t) = V₀ . (3.23)

Всі інші форми динаміки захворювання знаходяться між (3.22) і (3.23). Нехай у момент t = 0 в організм проникає доза V₀ антигена і  > F^* (порушується умова стійкості стаціонарного розв’язку стану здорового організму). Тоді початкові умови мають вигляд

V(0) = V⁰, C(0) = C ^*, F(0) = F ^*, m(0) = 0.

Концентрація антигена починає рости, оскільки V⁰(0) > 0 і  - F⁰ =  - F ^* > 0. Якщо не наступає летального наслідку, то для деякого t₁ > 0 значення V(t₁) = V_max. Оскільки (t₁) = 0, то  - F(t₁) = 0 і F(t₁) =  / . Для t > t₁ F(t) >  /  і V(t) спадає, поки F(t) >  / , бо тоді (t) < 0.

Якщо F(t) >  /  на досить великому інтервалі (t₁, t₂), то V(t) спадає на цьому інтервалі майже до нуля (рис. 3.11).

Рис. 3.11. Гостра форма захворювання

Розв’язок такого типу назвемо гострою формою захворювання. Якщо інтервал (t₁, t₂) досить вузький, то у точці t₂, де F(t₂) =  /  функція V(t) досягає V_min, але на набуває малих значень. Для t > t₂  - F(t) < 0, тому V(t) знову починає рости в відбувається чергування локальних мінімумів і максимумів. Розв’язки такого типу називаються хронічною формою хвороби (рис. 3.12).

Хронічна форма хвороби обумовлена недостатньо ефективною реакцією імунної системи. Це випливає з того, що при слабкій реакції імунної системи ( - мале, запізнення  - велике; значне ураження органу), з одного боку підвищується V_max, а з іншого – зменшується F_max, внаслідок чого звужується інтервал (t₁, t₂).

Якщо не пройдений імунологічний бар’єр: V⁰ < V^* і  - F^*< 0, то можливий випадок (t) < 0 для t > 0, що відповідає субклінічній формі хвороби. Якщо ж  - F^* > 0 і (t) > 0 для t > 0, то маємо летальний наслідок.

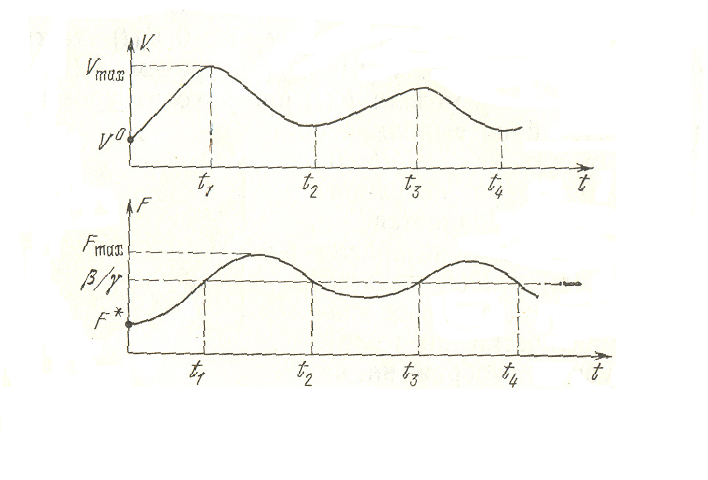
Рис. 3.12. Хронічна форма захворювання

Отже, модель (3.1)-(3.6) дозволяє класифікувати всі форми інфекційного захворювання.