3.3. Проста модель інфекційного захворювання

Проста модель інфекційного захворювання розглядається як деяка математична абстракція. Вона не описуватиме яких-небудь конкретних захворювань, що спричинені певним антигеном. Основна задача математичного моделювання – опис і пошук найбільш загальних зако-номірностей, характерних для всіх інфекційних захворювань. Ця модель побудована Г.І. Марчуком у 1975 р. [7]. У монографії [1, с. 57-59] висвітлено історію питання й наведено відповідні посилання.

Під інфекційним захворюванням розуміють відображення взаємодії, яка встановилась між двома членами біоценозу, один з яких здатний завдяки механізмам патогенності існувати в іншому, а інший завдяки механізмам захисту виявляти протидію патогенній дії. Одним із головних засобів захисту організму від інфекції є система імунітету. Суть імунної реакції на проникнення генетично чужорідного матеріалу (антигенів), зокрема вірусів чи бактерій, полягає у продукуванні специфічних матеріальних об’єктів (антитіл, клітин-кіллерів), здатних нейтралізувати або знищувати антигени. У простій моделі виділяються наступні суттєві характеристики захворювання.

1.Кількість (концентрація) збудників хвороби V(t), тобто антигенів, які здатні розмножуватись.

2. Кількість (концентрація) антитіл F(t), здатних нейтралізувати антигени (імуноглобуліни, рецептори імунокомпетентні клітини, -лімфоцити).

3. Кількість (концентрація) плазмоклітин C(t), які є носіями і проду-центами антитіл.

4. Відносна характеристика ураження органу-мішені m(t). Якщо М–характеристика здорового органу (маса або площа), а – та ж харак-теристика здорової частини ураженого органу, то

.

Для неураженого органу m= 0, а для повністю ураженого m= 1.

Проста модель орієнтована на індивідуума із великої усередненої групи інфікованих, індивідуальні особливості перебігу захворювання якого не врахо-вуються, і будується на співвідношенні балансу для кожного з факторів, що беруть участь в імунному процесі. Тому часткові особливості функціонування імунної системи не є істотними для аналізу динаміки захворювання, а на першому плані виступають основні закономірності перебігу захисної реакції організму.

Будемо розглядати інфекційне захворювання як конфлікт між популяцією збудника хвороби та імунною системою організму, де антигени –“жертви”, а антитіла –“хижаки”. Тому рівняння для V(t), як і в моделі Вольтерри -Лотки, набуває вигляду

, (3.1)

де – швидкість (темп) розмноження антигена, -коефіцієнт, який враховує ймовірність зустрічі антигенів із антитілами та силу їх взаємодії.

Для складання наступного рівняння, яке описуватиме ріст плазматичних клітин, скористуємось гіпотезою формування каскадних популяцій таких клі-тин [1, с.18-22]. Імунокомпетентний В-лімфоцит стимулюється комплексом антигена із – рецептором у присутності сигналу від специфічного Т- лімфоцита-помічника, активованого антигеном на макрофагах. Це дає початок каскадному процесу утворення клітин, які синтезують антитіла для нейтралізації антигенів даного виду. Число лімфоцитів, що стимулюються таким чином, буде пропорційним VF. Отже, приріст плазмаклітин над нормальним рівнем C* – постійним рівнем плазмоклітин у здоровому організмі

,

де перший доданок описує утворення плазмоклітин, час формування каскаду плазмоклітин, коефіцієнт стимулювання імунної системи. Коефіцієнт враховує ймовірність зустрічі антиген – антитіло, збудження каскадної реакції і число нових клітин, які утворюються. Коефіцієнт описує зменшення числа плазмоклітин внаслідок старіння і пропорційний оберненій величині їх часу життя. В підсумку одержимо рівняння

. (3.2)

Для складання рівняння для F підрахуємо баланс числа антитіл, які реагують із антигеном, виходячи із співвідношення

Перший доданок описує утворення антитіл за відрізок часу dt, –швидкіть утворення антитіл однією плазмоклітиною. Другий доданок описує зменшення числа антитіл на відрізку часу dt за рахунок зв’язування із антигенами, – кількість антитіл, необхідних для нейтралізації одного антигена. Доданок описує зменшення популяції антитіл внаслідок старіння, коефіцієнт обернено пропорційний тривалості життя антитіла. Поділивши на dt одержимо третє рівняння:

. (3.3)

Ураження органу-мішені веде до зменшення активності органів, які забезпечують поставку лейкоцитів, макрофагів тощо Приймемо гіпотезу про те, що продуктивність органів імунної системи зв’язана із розмірами органу-мішені і запишемо четверте рівняння у вигляді

(3.4)

Тут коефіцієнт >0 описує темп ураження органу, а >0 –швидкість відновлення маси ураженого органу і пропорційний оберненій величині періоду відновлення органу.

Система рівнянь (1)-(4) називається простою моделлю інфекційного захворювання і побудована у 1975 р. [4] (див. також [2,3]). В рамках цієї моделі в момент часу в організм проникає початкова популяція вірусу , де вона починає розмножуватись у клітинах органу – мішені й уражати його. Частина антигенів попадає в кров, де взаємодіє із рецепторами імунокомпетентних клітин і внаслідок цього відбувається стимулювання імунної системи. Через час формується каскад плазмоклітин, які виробляють антитіла, специфічних до антигенів. Антитіла зв’язують віруси і від їх боротьби між ними залежить перебіг захворювання та його наслідки. Якщо антиген встигає значно уразити тканину органу, то погіршується загальний стан організму і як наслідок, робота імунної системи. Зауважимо, що

. (3.5)

Якщо m(t)=1, то орган мішень повністю уражений і наступає летальний наслідок. Врахувати ураження органу можна, замінивши у рівнянні (3.2) коефіцієнт на Типовий вигляд функції показаний на рис. 3.10.

(3.6)

Для різних хвороб значення і відповідно для може відрізнятися, але якісно відповідатиме схемі на рис. 3.10. Оцінкою значення є 0.15-0.20.

Задамо початкові умови для простої моделі(1)-(4):

V(0)= . (3.7)

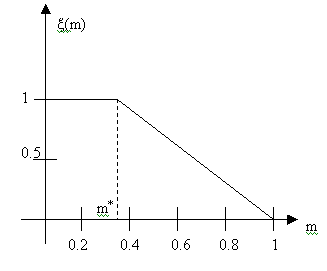
Рис.3.10. Вплив ураження органу на імунну відповідь

Вважатимемо, що проникання антигену відбувається в момент t=0, тому

V(t)=0, t [- ,0). (3.7₁)

Зауважимо, що в моделі фігурує об’єднана популяція плазмоклітин C(t). Якщо антигени відсутні в організмі, то C(t)= . Якщо =0, то організм толерантний по відношенню до даного антигена.