6.7. Анализ чувствительности транспортной модели

Напомним, что элементы транспортной таблицы — стоимости перевозок формально являются коэффициентами целевой функции, объемы спроса и предложения — правыми частями ограничений математической модели транспортной задачи, а каждой клетке транспортной таблицы соответствует переменная.

Анализ чувствительности позволит определить, в каких пределах могут изменяться эти параметры при условии неизменности оптимального плана.

1. Изменение стоимости перевозки для незанятой клетки.

Для определения пределов изменения необходимо придать стоимости изменение , вычислить новую оценку для той клетки, стоимость перевозки которой изменилась, и записать условие оптимальности плана — неположительность этой оценки, это даст нам необходимое неравенство

2. Изменение стоимости перевозки для занятой (базисной) клетки.

Изменение стоимости влияет на потенциалы, поэтому необходимо придать стоимости изменение , затем вычислить новые потенциалы и новые оценки всех свободных клеток. План останется оптимальным до тех пор, пока оценки всех свободных клеток неположительны — это даст нам необходимые неравенства.

3. Одновременное увеличение объема производства и спроса.

а) Если одновременно на увеличиваются объемы пункта производства и пункта потребления которым соответствует ненулевая перевозка, то ее значение просто увеличивается на величину .

б) ) Если одновременно на увеличиваются объемы пункта производства и пункта потребления между которыми нет перевозки, то необходимо составить цикл, начинающийся в рассматриваемой свободной ячейке, вершинами которого являются занятые ячейки. Вершинам цикла приписываются знаки: вершине, соседней со свободной— плюс, следующей — минус и т.д. Затем значения перевозок в положительных вершинах увеличиваются на , а значения перевозок в отрицательных вершинах — уменьшаются на . Заметим, что при этом состав занятых ячеек не изменяется, изменяются значения переменных в них.

6.8. Задача о назначениях

Задача о назначениях является частным случаем транспортной задачи, но, учитывая ее специфику, для ее решения разработаны специальные методы решения.

Имеется исполнителей, которые могут выполнить различных работ. Известна стоимость (затраты, издержки) от выполнения -м исполнителем -й работы ( ). Необходимо так назначить исполнителей на работы, чтобы добиться минимальной суммарной стоимости такого назначения при условии, что каждый исполнитель может быть назначен только на одну работу и каждую работу может выполнять только один исполнитель.

Для построения математической модели обозначим через факт назначения или неназначения -го исполнителя на -ю работу, а именно:

С учетом обозначений математическая модель задачи о назначениях имеет вид:

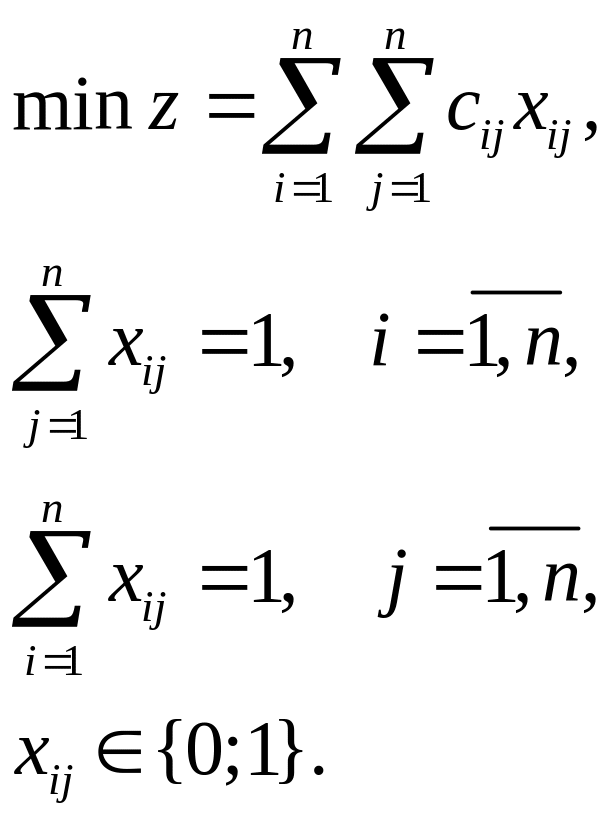
Для решения задачи о назначениях можно воспользоваться методом Фогеля или венгерским методом. Венгерский метод является модификацией симплекс-метода и основывается на том, что оптимальное решение задачи не изменится, если ко всем элементам какой-либо строки или столбца матрицы стоимостей прибавить или вычесть константу.

Венгерский метод.

1. В исходной матрице стоимостей для каждой строки определяется минимальный элемент и вычитается из всех элементов строки.

2. В матрице, полученной на предыдущем шаге, для каждого столбца определяется минимальный элемент и вычитается из всех элементов этого столбца.

3. Так как мы рассматриваем задачу на минимум, то оптимальному назначению соответствуют нулевые элементы матрицы, полученной на предыдущем шаге.

4. В некоторых случаях нулевые элементы, полученные в матрице стоимостей на предыдущих шагах, не позволяют непосредственно получить решение. В этом случае необходимо:

   1. В последней матрице, полученной выше, провести минимальное число горизонтальных и вертикальных линий по строкам и столбцам так, чтобы вычеркнуть в матрице все нулевые элементы;

   2. Найти наименьший невычеркнутый элемент, вычесть его из всех невычеркнутых элементов и прибавить к элементам, стоящим на персечении проведенных на предыдущем шаге линий.

   3. Произвести назначение на нулевые элементы матрицы стоимостей. Если это невозможно — повторить шаг 4.