Раздел 9. Ряды.

§1. Числовые ряды. Основные понятия.

Пусть дана бесконечная числовая последовательность

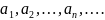
Выражение вида называется числовым рядом.

- члены ряда, 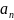- общий член ряда (некоторая функция от номера).

Сумма конечного числа n - первых членов ряда называется n -ой частичной суммой ряда: , , …, ,…

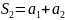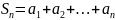Частичные суммы 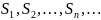образуют бесконечную последовательность.

Числовой ряд называется сходящимся, если существует конечный предел последовательности частичных сумм: 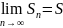, при этом 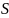- сумма ряда.

Если предел последовательности частичных сумм не существует, или бесконечен, то ряд называется расходящимся.

Примеры.

1)

(арифметическая прогрессия),

ряд расходится

2)

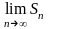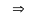не существует ряд расходится.

3)

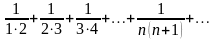
Так как 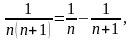то

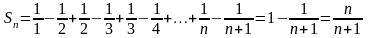
ряд сходится.

4) 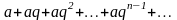- геометрический ряд.

(сумма геометрической прогрессии).

а) при получим ряд сходится;

б) при 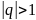получим ряд расходится;

в) при получим ряд расходится;

г) при 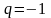получим не существует ряд расходится.

Таким образом, геометрический ряд сходится только при

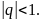
Необходимое условие сходимости.

Теорема (необходимое условие сходимости). Если ряд сходится, то .

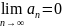(доказательство самостоятельно)

Данное условие не является достаточным, то есть может , но ряд расходится.

Пример.

Гармонический ряд:

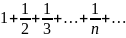
, но ряд расходится. Покажем это.

Предположим противное – данный ряд сходится и его сумма . Тогда:

и . Тогда

Но .

Противоречие, ряд расходится.

Следствие. Если , то ряд расходится.

n - остатком ряда называется ряд, образованный членами ряда, не входящими в n-ую частичную сумму: .

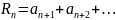Свойства сходящихся рядов.

Теорема 1. У сходящегося ряда .

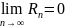Теорема 2. Отбрасывание конечного числа первых членов ряда не влияет на его сходимость.

Теорема 3. Если ряд сходится и его сумма равна , то ряд , где с некоторая постоянная, также будет сходиться и его сумма равна .

Теорема 4. Если ряды и сходятся, и их суммы равны и соответственно, то ряды 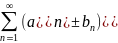будут сходиться, и их суммы равны .

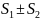Теорема 5. В сходящемся ряде можно объединять члены ряда в произвольные группы, не нарушая порядка членов ряда.

Знакопостоянные ряды.

Ряд, все члены которого имеют одинаковые знаки, называют знакопостоянным рядом. Ряд, все члены которого положительны, называют знакоположительным рядом. Знакоположительный ряд – частный случай знакопостоянного ряда.

Достаточные признаки сходимости знакоположительных рядов.

Первый признак сравнения.

Пусть ряды и такие, что . Тогда, из сходимости ряда следует сходимость ряда , из расходимости ряда следует расходимость ряда .

Пример.

Исследовать на сходимость ряд

Сравним с геометрическим рядом (сходящимся) .

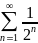Для любого n выполняется: . Тогда из сходимости ряда следует сходимость исходного ряда .

Второй признак сравнения.

Если существует конечный, отличный от 0, 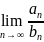, то ряды и (где одновременно сходятся или расходятся.

Пример.

Исследовать на сходимость ряд .

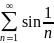Сравним с гармоническим рядом (расходящимся) .

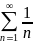(по первому замечательному пределу), следовательно, ряды и одновременно расходятся.

Замечание. В качестве ряда для сравнения необходимо брать такой ряд, чтобы основная структура исходного ряда сохранялась, сравниваемый ряд был проще, было известно, сходится он или расходится. Эталонные ряды для сравнения: геометрический ряд (сходится при ); обобщенный гармонический ряд (сходится при

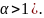
Признак Даламбера.

Если для ряда (где 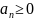) существует , то:

1. при ряд расходится;

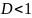2. при ряд сходится;

3. при вопрос остается открытым.

Примеры.

1. Исследовать на сходимость ряд

Следовательно, исходный ряд сходится.

2. Исследовать на сходимость ряд

Следовательно, исходный ряд сходится.

Предельный признак Коши.

Если для ряда (где ) существует , то:

1. при 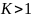ряд расходится;

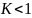2. при ряд сходится;

3. при вопрос остается открытым.

Пример.

Исследовать на сходимость ряд .

.

Следовательно, исходный ряд сходится.

Интегральный признак Коши.

Пусть члены ряда (где 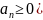являются при 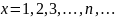значениями непрерывной, невозрастающей на функции. Тогда ряд и несобственный интеграл (где ) одновременно сходятся или расходятся.

Пример.

Исследовать на сходимость гармонический ряд

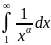при сходится. Следовательно, исходный ряд также сходится при .