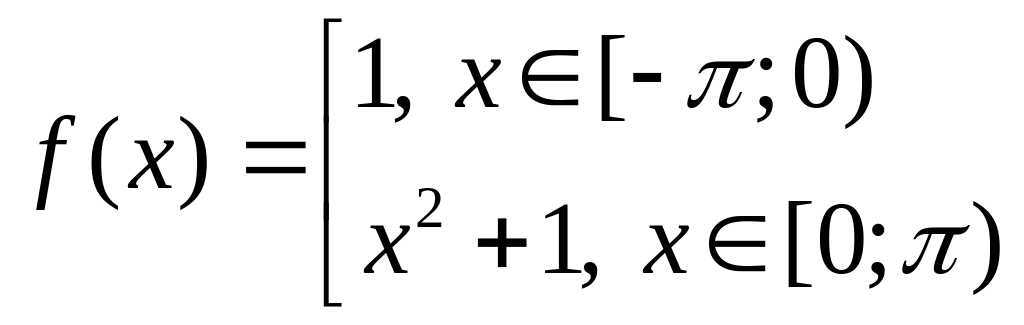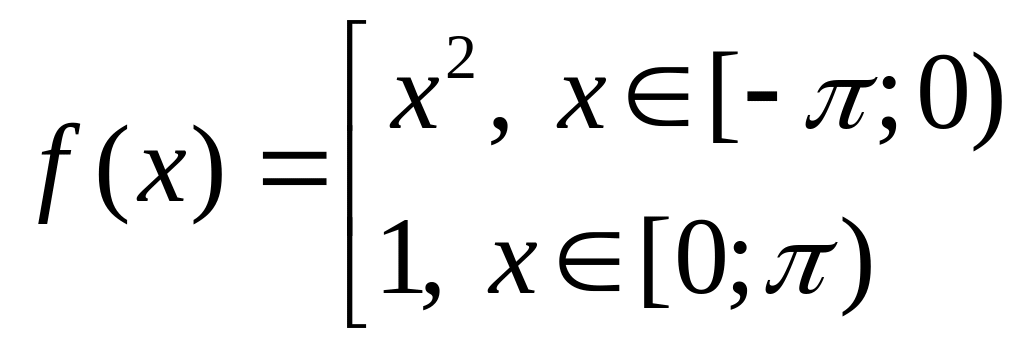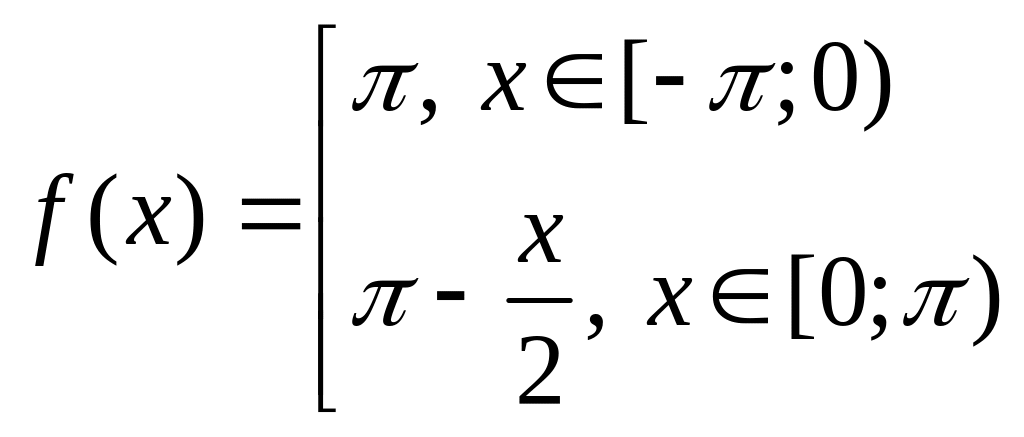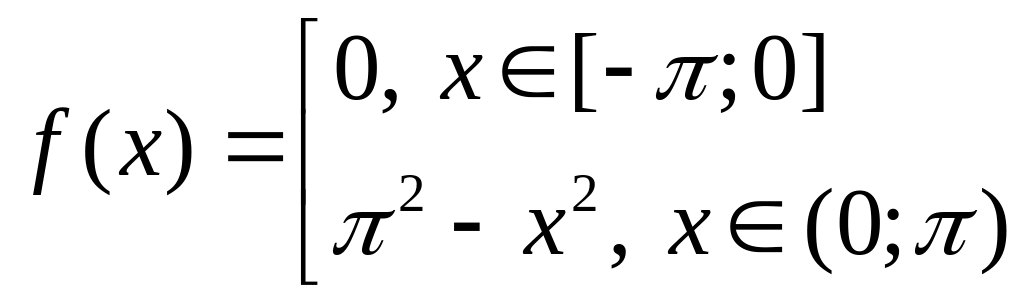Задача 5

Составить представление функции интегралом Фурье. Найти преобразования Фурье и определить амплитудный спектр функции .

Решение

1. Построим график заданной функции :

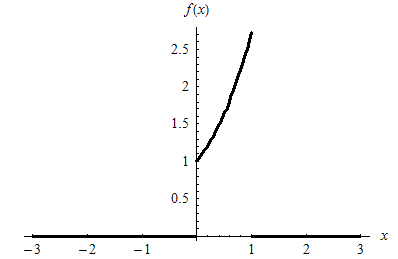
Данная функция f(x) на каждом отрезке [-l,l], где l – любое число, кусочно-монотонная (в нестрогом смысле), кроме того, f(x) – абсолютно интегрируемая функция, т.е. сходится несобственный интеграл . Таким образом, функция может быть представлена интегралом Фурье.

2. Составим представление функции интегралом Фурье в действительной форме, которое имеет следующий теоретический вид:

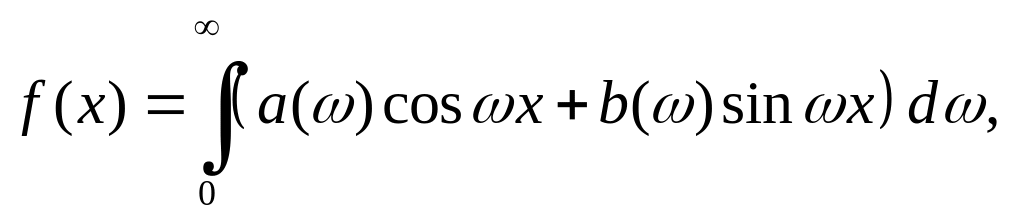где

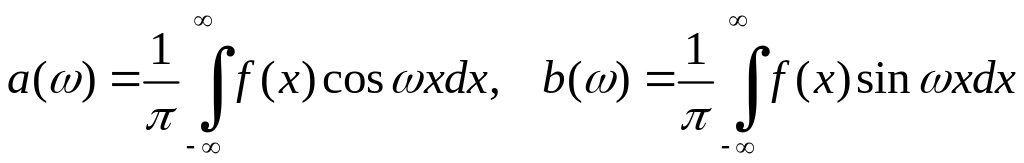(1)

Вычисляем

1) если , то

;

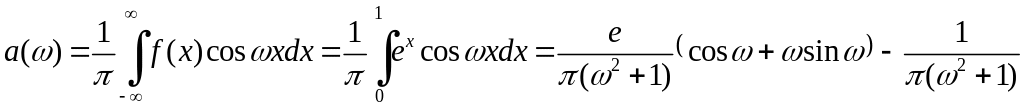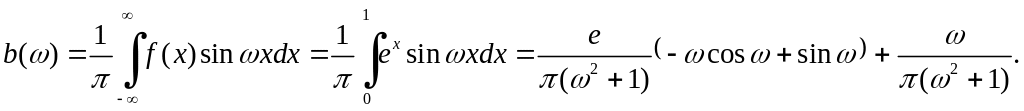
Вычисление интегралов методом интегрирования по частям:

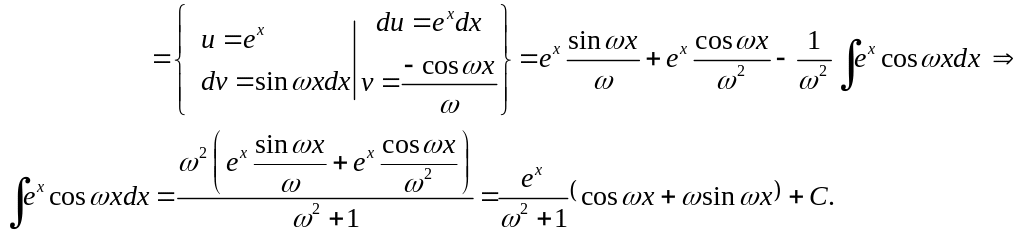
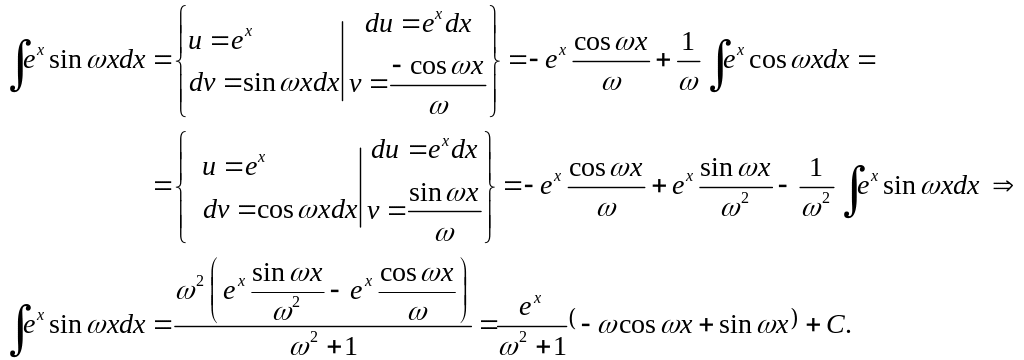
2) если , то

; ;

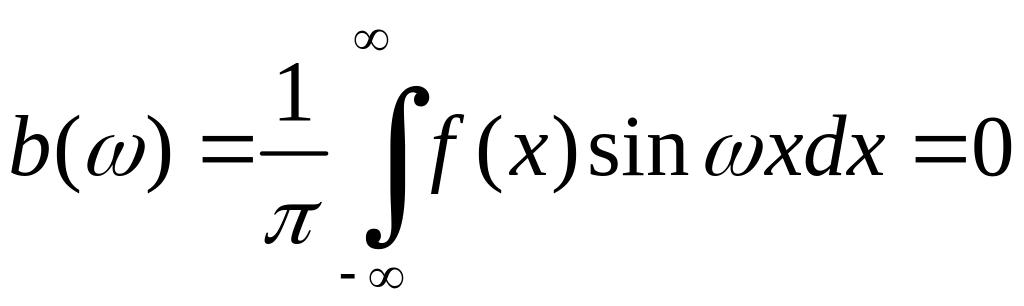эти же значения могут быть получены посредством предельного перехода в предыдущих формулах для ( ).

Подставляя функции в равенство (1) получаем представление данной функции интегралом Фурье в действительной форме:

(2)

Составленный несобственный интеграл гарантированной сходится к функции , которая составляется по теореме Дирихле и отличается от функции только в точках скачкой;

в решаемой задаче имеет вид:

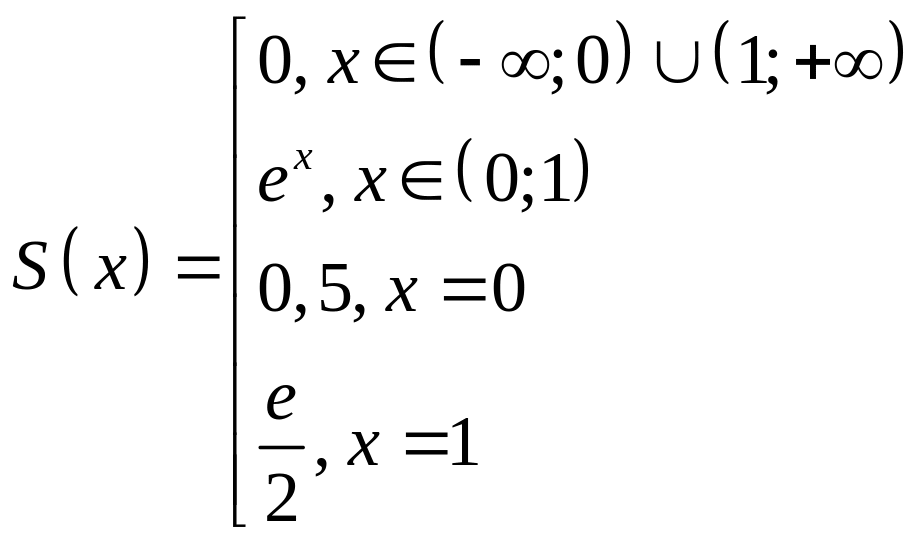
3. Комплексная форма интеграла Фурье имеет теоретический вид:

.

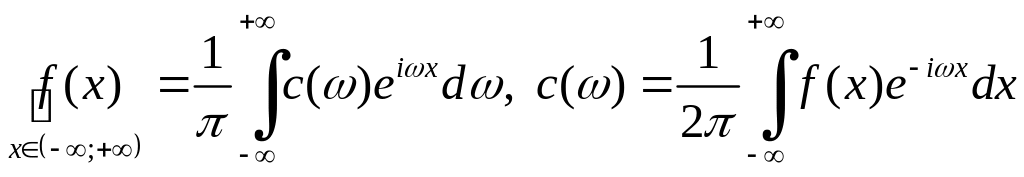Вычисляем :

.

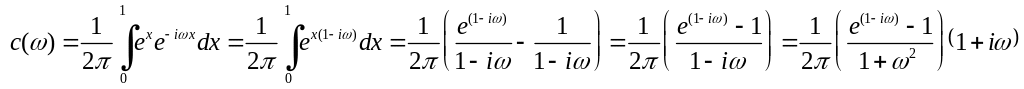Подставляя получаем представление той же функции интегралом Фурье в комплексной форме:

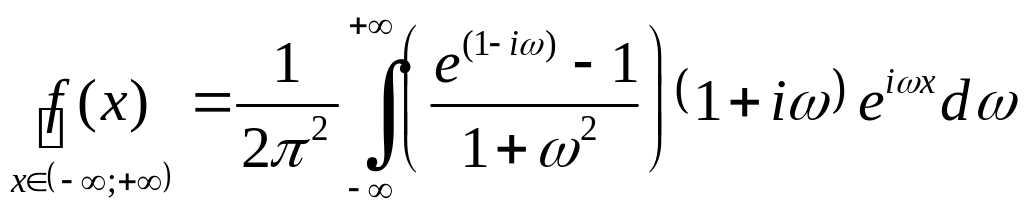. (3)

4. Запишем косинус-преобразование Фурье , синус-преобразование Фурье и комплексное преобразование Фурье данной функции :

,

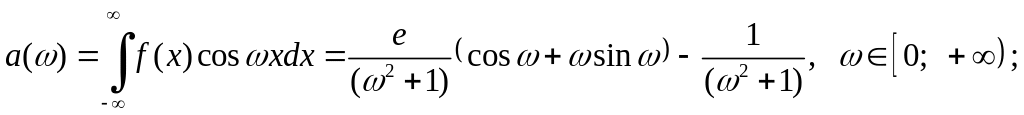
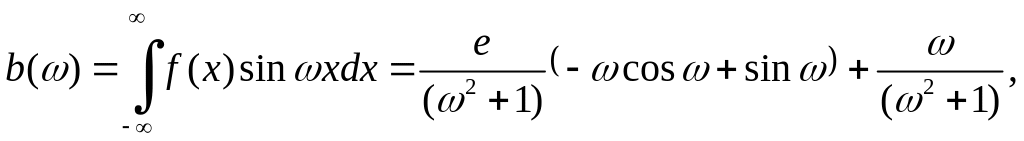
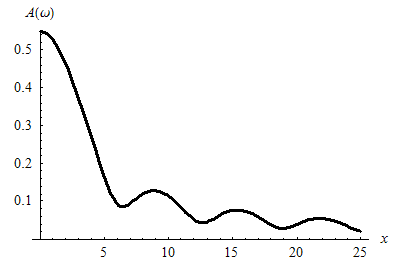
5. Определим непрерывный амплитудный спектр данной функции , построим его график.

Амплитудный спектр для действительной формы (2) интеграла Фурье:

график амплитудного спектра:

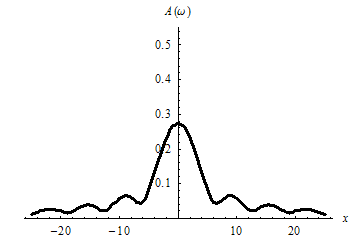
Амплитудный спектр для комплексной формы (3) составленного интеграла Фурье:

график амплитудного спектра в этом случае:

Ответ:

1) Представление интегралом Фурье в действительной форме:

представление интегралом Фурье в комплексной форме:

.

2) Преобразования Фурье функции :

(косинус-преобразование);

(синус-преобразование);

, (комплексное преобразование).

3) амплитудный спектр функции :

, ;

, .

Приложение А. Образец оформления титульного листа

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ

ФГОУ ВПО «Мурманский государственный технический университет»

Кафедра ВМ и ПО ЭВМ

Расчетно-графическое задание

«Ряды Фурье. Интеграл Фурье»

по дисциплине «Специальные разделы высшей математики»

выполнил: студент группы П-271(1)

Запорожцев И.

проверил: доцент кафедры

Кацуба В.С.

оценка: _____________________

дата: _____________________

Мурманск

2008

Выполнить ВАРИАНТ №7

Приложение Б. Варианты заданий

Варианты задач

Задача 1 Разложить в ряд Фурье периодическую функцию с периодом . Записать сумму ряда.

План решения задачи

1. Построить график функции , и ее периодического продолжения. Проанализировать возможность разложения в ряд Фурье.

2. Записать вид ряда Фурье для , и формулы для коэффициентов ряда.

3. Вычислить коэффициенты ряда , и .

4. Записать сумму ряда , по теореме Дирихле.

5. Подтвердить достоверность разложениия.

Варианты

1.	2.	3.
4.	5.	6.
7.	8.	9.
10.	11.	12.
13.	14.	15.
16.	17.	18.
19.	20.	21.
22.	23.

Задача 2 Разложить в ряд Фурье функцию с периодом . Построить график суммы ряда .

План решения задачи

1. Построить график функции , и ее периодического продолжения. Проанализировать возможность разложения в ряд Фурье.

2. Записать вид ряда Фурье для , и формулы для коэффициентов ряда.

3. Вычислить коэффициенты ряда , и .

4. Записать сумму ряда , по теореме Дирихле.

5. Построить график суммы ряда , .

6. Подтвердить достоверность разложения.

Варианты

1.	, ,	2.	, ,	3.	, ,
4.	, ,	5.	, ,	6.	, ,
7.	, ,	8.	, ,	9.	, ,
10.	, ,	11.	, ,	12.	, ,
13.	,	14.	, ,	15.	, ,
16.	,	17.	, ,	18.	, ,
19.	, ,	20.	, ,	21.	,
22.	, ,	23.	, ,

Задача 3 Составить ряд Фурье по синусам (косинусам), сходящийся на интервале к значениям функции .

План решения задачи