
- •1. Общие организационно-методические указания
- •2. Задание, план выполнения, требования к оформлению отчета
- •Содержание задач каждого варианта:
- •Общие требования к оформлению ргз:
- •План выполнения ргз:
- •3. Список рекомендуемых источников
- •4. Образец варианта заданий ргз по теме «Интегральное исчисление фнп. Элементы теории полей» Вариант 1
- •5. Пример выполнения ргз
- •Задача 3
- •Задача 4
- •Задача 5
- •Записать вид ряда Фурье для , и формулы для коэффициентов ряда.
- •Вычислить коэффициенты ряда , и .
1. Общие организационно-методические указания
РГЗ включает в себя основные практические задачи по теме «Элементы гармонического анализа (ряды Фурье, интеграл Фурье)» дисциплины «Специальные разделы высшей математики» и предназначена для студентов второго курса специальности 230105.65 «ПО МВ и АС».
Целевая установка: при выполнении РГЗ студент должен показать усвоенный материал по представлению функций тригонометрическими рядами Фурье или интегралами Фурье, знать условия, при которых эти представления возможны, и уметь подтвердить полученные представления построением графиков с использованием ПП «Mathematica».
2. Задание, план выполнения, требования к оформлению отчета
РГЗ содержит 5 задач, из которых первые 4 относятся к рядам Фурье, а пятая – к интегралам Фурье. К каждой задаче прилагается план ее решения.
Содержание задач каждого варианта:
разложить в ряд Фурье
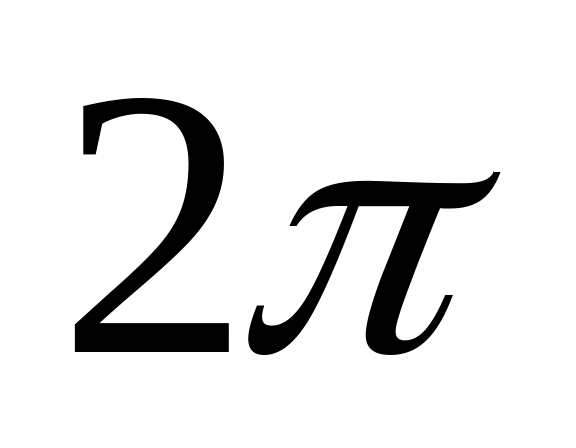 - периодическую функцию и записать
сумму полученного ряда по теореме
Дирихле;
- периодическую функцию и записать
сумму полученного ряда по теореме
Дирихле;разложить в ряд Фурье
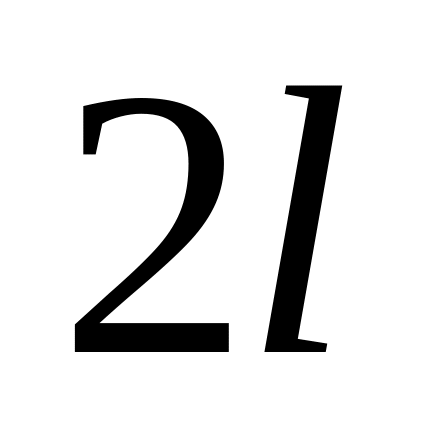 - периодическую функцию и построить
график суммы полученного ряда;
- периодическую функцию и построить
график суммы полученного ряда;составить ряд Фурье по синусам или косинусам, сходящийся на промежутке
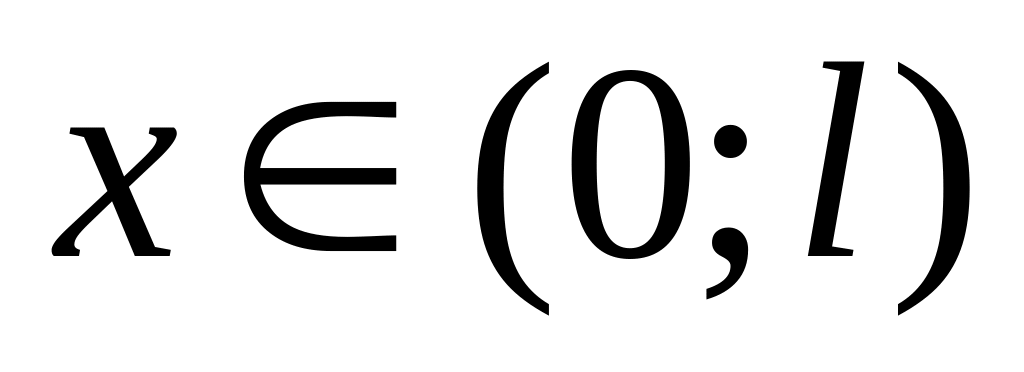 к значениям заданной функции;
к значениям заданной функции;составить ряд Фурье в комплексной форме для функции
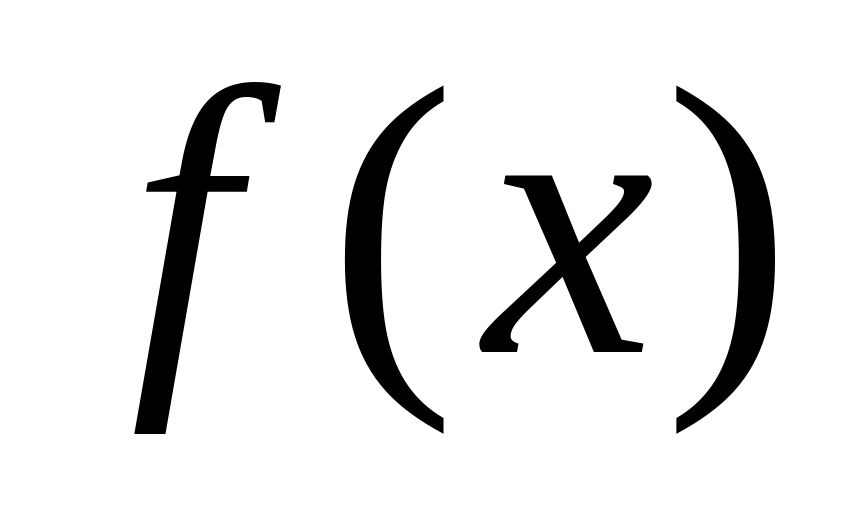 ,
периодической с
,
периодической с
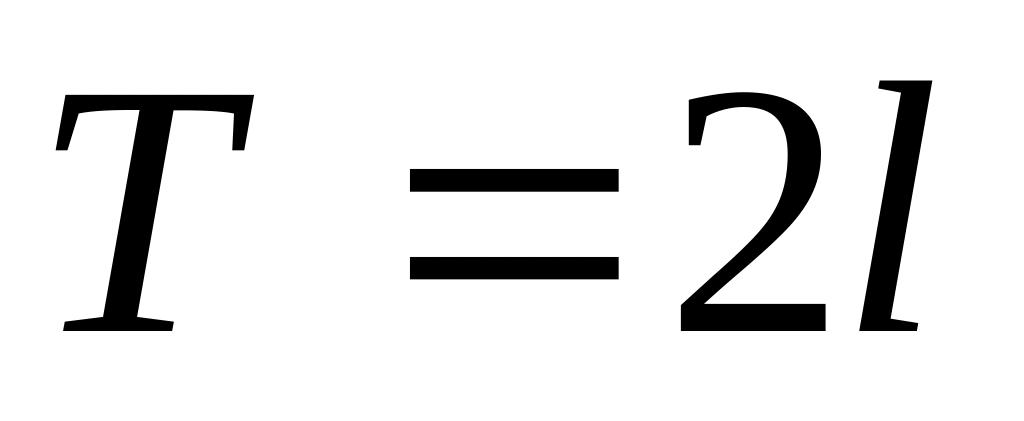 ;
определить дискретный амплитудный
спектр функции
;
;
определить дискретный амплитудный
спектр функции
;составить представление функции ,
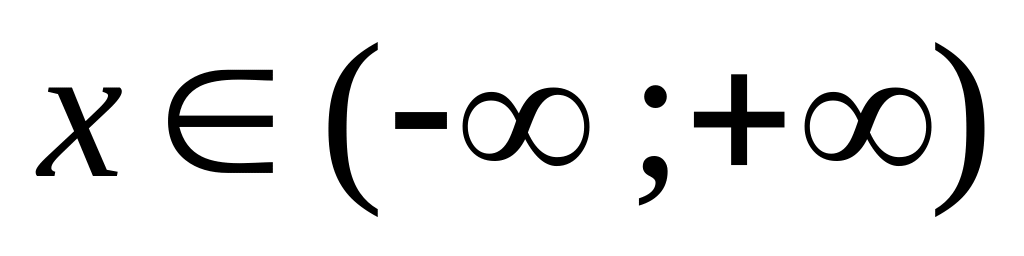 интегралом Фурье; записать преобразования
Фурье этой функции и определить ее
амплитудный спектр.
интегралом Фурье; записать преобразования
Фурье этой функции и определить ее
амплитудный спектр.
Общие требования к оформлению ргз:
каждая задача должна иметь условие, подробное решение и ответ;
в решении нужно ссылаться на теоретические факты (из темы РГЗ), на основании которых строится решение;
построение чертежей (или рисунков), приведение подробных выкладок в решении обязательно.
План выполнения ргз:
РГЗ выдается в начале прохождения темы, выполняется по мере изучения темы и сдается преподавателю практических занятий после завершения темы на практических занятиях;
преподавателем может назначаться защита РГЗ всей группе или отдельным студентам.
3. Список рекомендуемых источников
Конспект лекций ведущего преподавателя дисциплины.
Письменный Д.Т. Конспект лекций по высшей математике. 2 часть. – М.: Рольф, 2000.– 256с.
Данко П.Б., Попов А.Г. Высшая математика в упражнениях и задачах. В 2-х частях. Часть II: Учебное пособие для втузов. – М.: Высш. шк., 1997. – 416с.
Мостовской А.П. Информационные технологии в математике: Учебное пособие. – Мурманск: МГПУ, 2005. -16с.
Дьяконов В.П. Системы символьной математики Mathematica 2 и
Mathematica 3. – М.: СК Пресс, 1998. -328с.
4. Образец варианта заданий ргз по теме «Интегральное исчисление фнп. Элементы теории полей» Вариант 1
Задача 1
Разложить в ряд Фурье периодическую
функцию
![]() с периодом
с периодом
![]() .
Записать сумму ряда.
.
Записать сумму ряда.
План решения задачи
Построить график функции ,
 и ее периодического продолжения.
Проанализировать возможность разложения
в ряд Фурье.
и ее периодического продолжения.
Проанализировать возможность разложения
в ряд Фурье.Записать вид ряда Фурье для , и формулы для коэффициентов ряда.
Вычислить коэффициенты ряда
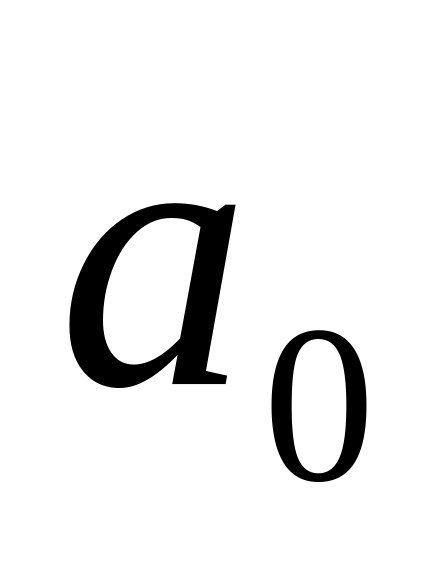 ,
,
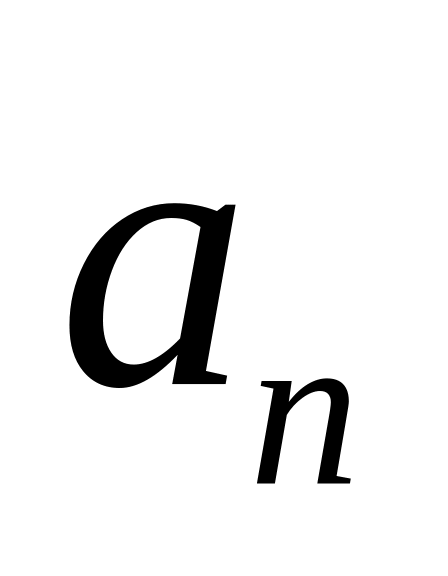 и
и
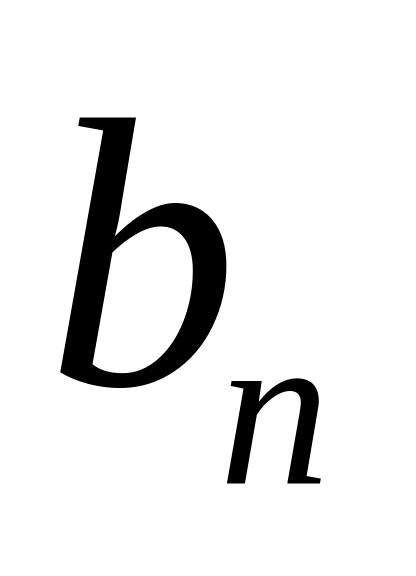 .
.Записать сумму ряда
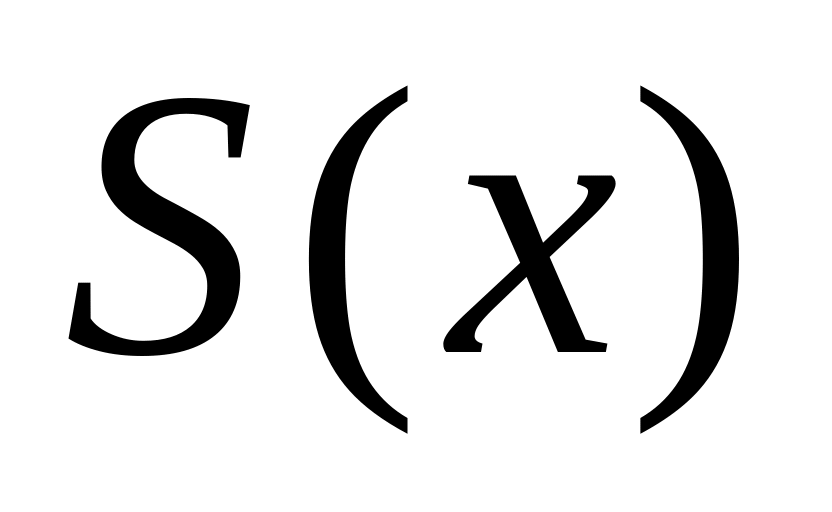 ,
,
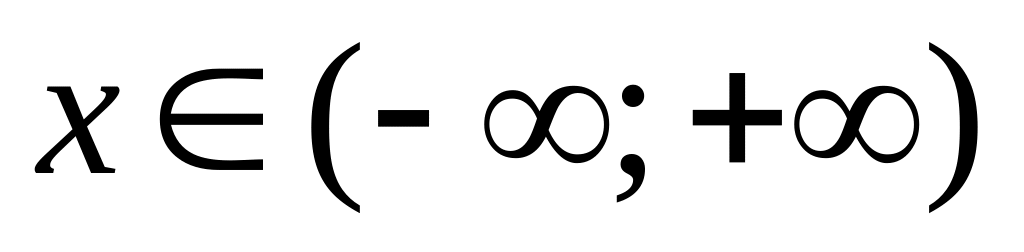 по теореме Дирихле.
по теореме Дирихле.Подтвердить достоверность.
Задача 2
Разложить в ряд Фурье функцию
![]() ,
,
![]() ,
,
![]() .
Построить график
.
Построить график
суммы ряда .
План решения задачи
Построить график функции ,
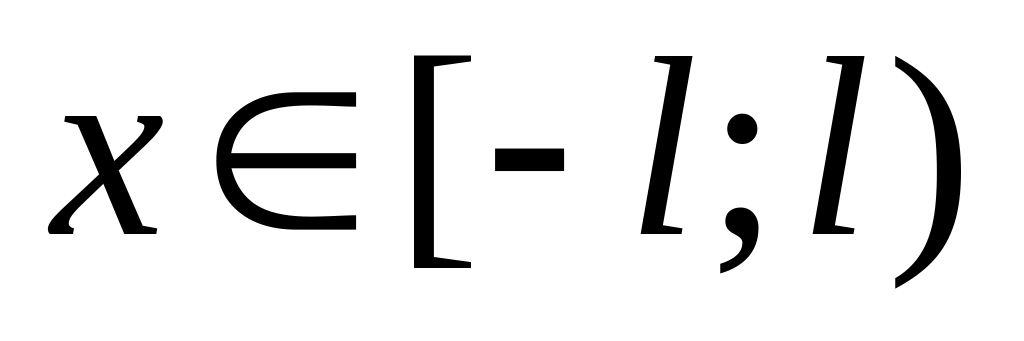 и ее периодического продолжения.
Проанализировать возможность разложения
в ряд Фурье.
и ее периодического продолжения.
Проанализировать возможность разложения
в ряд Фурье.Записать вид ряда Фурье для ,
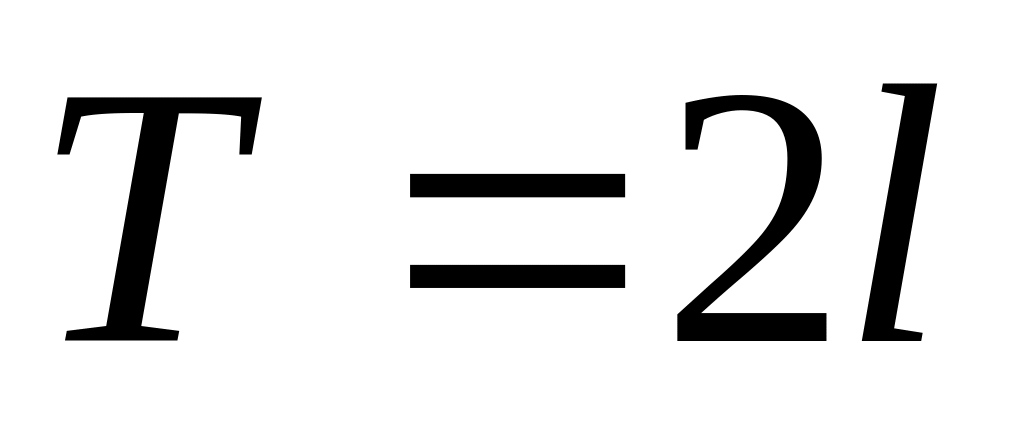 и формулы для коэффициентов ряда.
и формулы для коэффициентов ряда.Вычислить коэффициенты ряда , и .
Записать сумму ряда , по теореме Дирихле.
Построить график суммы ряда , .
Подтвердить достоверность.
Задача 3
Составить ряд Фурье по синусам ,
сходящийся на интервале
![]() к значениям функции
к значениям функции
![]() .
.
План решения задачи
Построить график функции , . Выполнить продолжение на интервал
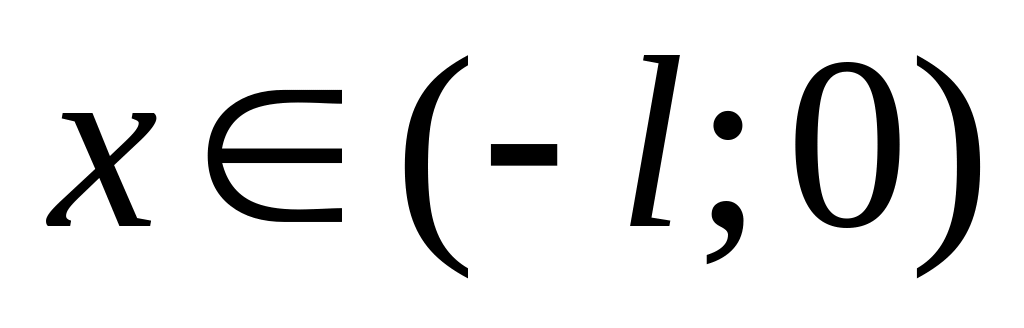 четным или нечетным образом. Построить
периодическое продолжение
,
.
четным или нечетным образом. Построить
периодическое продолжение
,
.Записать вид ряда Фурье для , и формулы для коэффициентов ряда.
Вычислить коэффициенты ряда , и .
Записать сумму ряда , .
Подтвердить достоверность.
Задача 4
Составить ряд Фурье в комплексной форме
для функции
![]() .
Определить амплитудный спектр функции.
.
Определить амплитудный спектр функции.
План решения задачи
Составить ряд Фурье в комплексной форме для функции ,
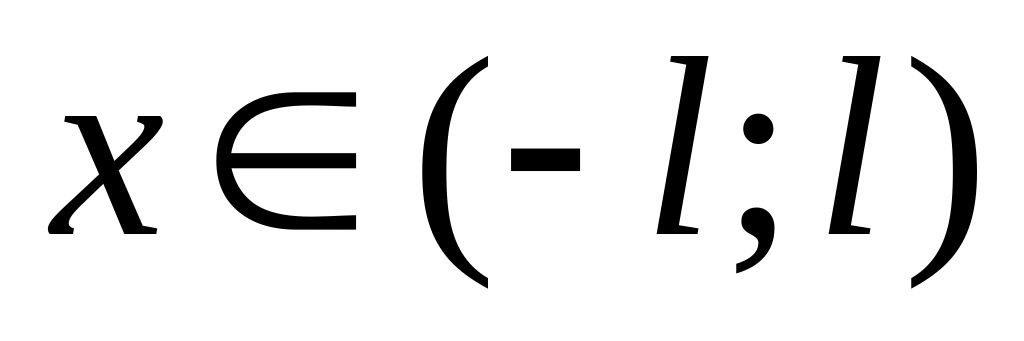 .
Записать сумму ряда
,
.
.
Записать сумму ряда
,
.Перейти от комплексной формы ряда Фурье к действительной форме.
Построить графики частичных сумм ряда
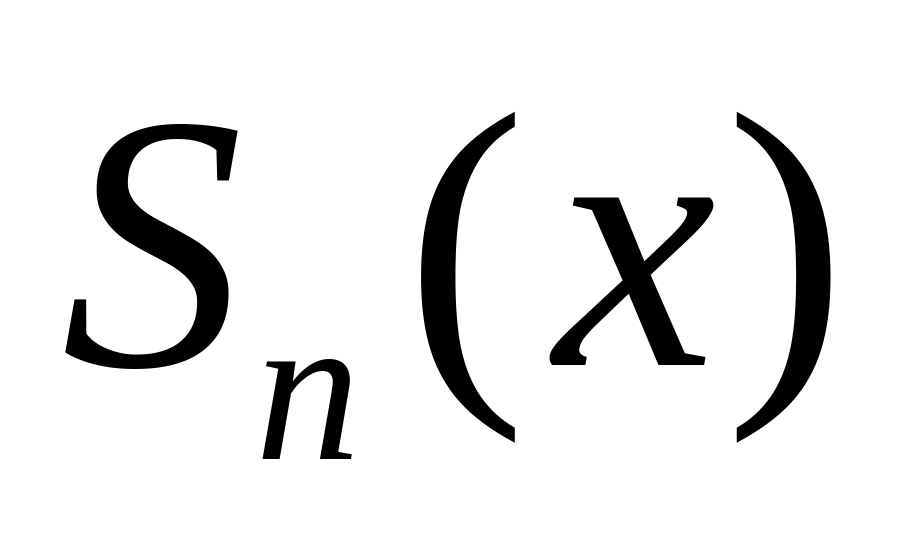 ,
,
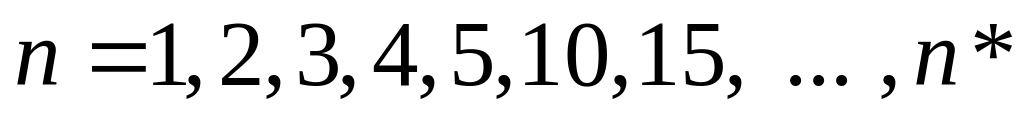 ,
где
,
где
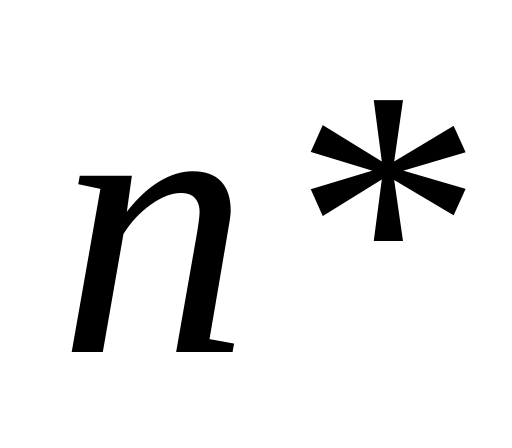 взять таким, чтобы
визуально была близка к
.
взять таким, чтобы
визуально была близка к
.Определить амплитудный спектр функции . Вычислить значения амплитуд
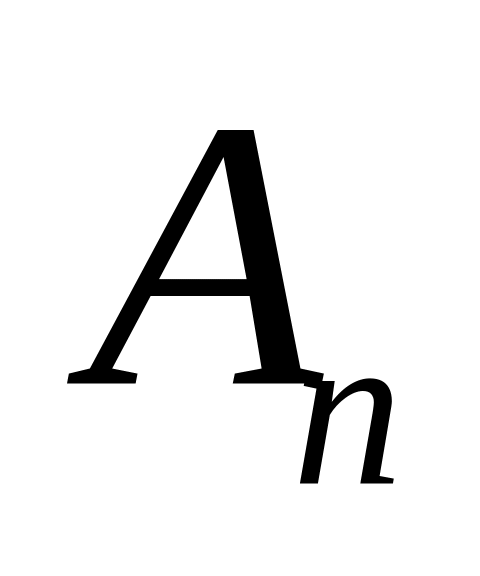 ,
.
Построить график
,
.
Построить график
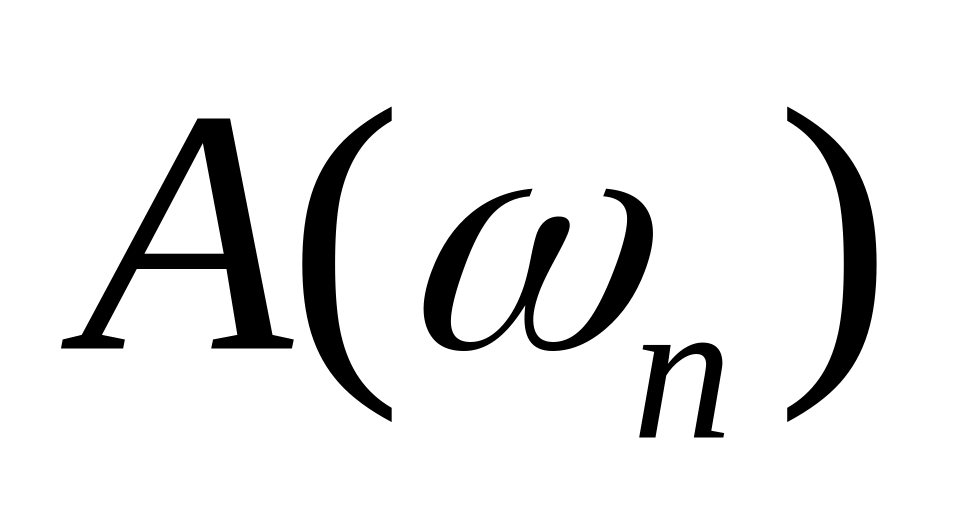 ,
где
,
где
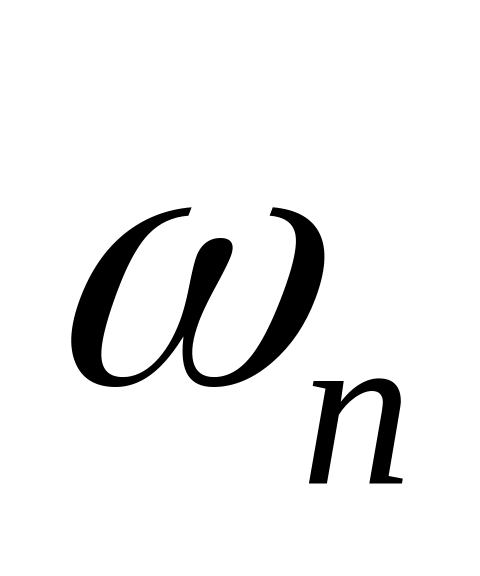 – частота.
– частота.
Задача 5
Составить представление функции
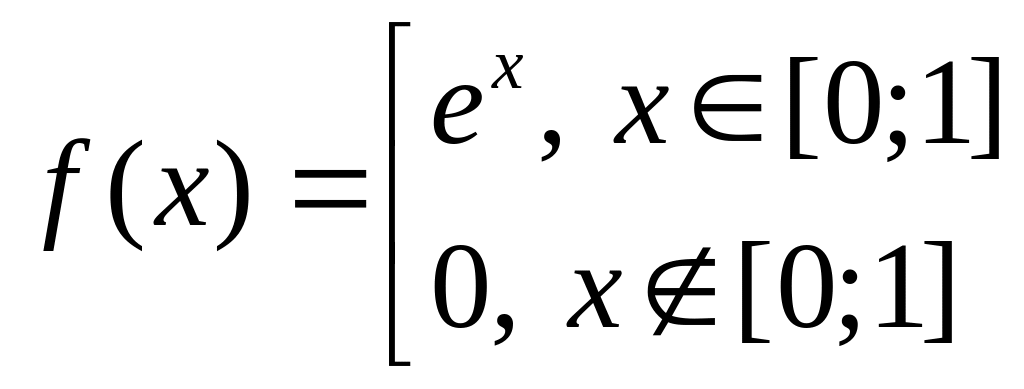 интегралом Фурье. Найти преобразования
Фурье и определить амплитудный спектр
функции
.
интегралом Фурье. Найти преобразования
Фурье и определить амплитудный спектр
функции
.
План решения задачи
Составить представление функции интегралом Фурье в действительной и комплексной формах.
Записать cos-преобразование, sin-преобразование и комплексное преобразование Фурье функции .
Определить амплитудный спектр
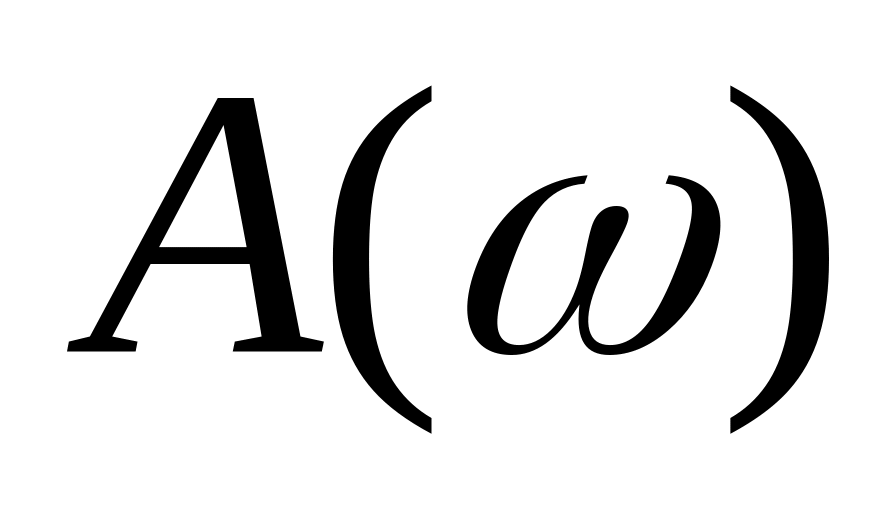 функции
,
построить его график.
функции
,
построить его график.
