3.2.2. Предельное сопротивление грунтов сдвигу. Закон Кулона.

Для изучения предельного сопротивления грунтов сдвигу, разработаны специальные приборы и методики испытаний. Наиболее распространенными в настоящее время являются сдвиговые приборы.

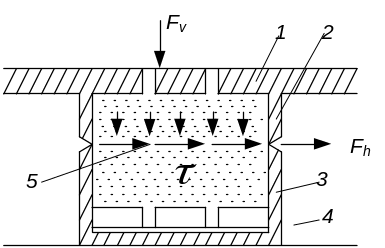
Рис.3.8. Схемы приборов прямого сдвига с нижней (а) и верхней (б) подвижными каретками: 1-штамп; 2-верхняя каретка; 3-нижняя каретка; 4-водоприемная камера; 5-зона принудительного среза.

Существует много конструктивных разновидностей сдвиговых приборов, среди которых можно выделить две группы:

1. приборы со ступенчатым загружением;

2. приборы с непрерывным загружением.

Испытанию подвергаются образцы грунта с ненарушенной структурой, иногда с нарушенной структурой, иногда с нарушенной с заданными исходными значениями плотности, влажности (напр. для песков).

Образец грунта помещается в металлическое кольцо, разделенное на части — подвижную и неподвижную обоймы. Подвижной может быть как нижняя, так и верхняя обоймы между обоймами до проведения опыта устанавливается небольшой зазор, который необходимо сохранять в течении всего опыта. Таким образом, создается фиксированная плоскость, по которой произойдет срез подвижной части грунта относительно неподвижной.

Вертикальное нормальное напряжение в плоскости сдвига создается с помощью рычажной системы в предположении, что нормальные напряжения в плоскости сдвига распределены равномерно, т. е. Вертикально приложенной силе, деленной на площадь образца. Нормальное напряжение сохраняется в течении всего опыта постоянным. Образец грунта до приложения сдвигающей силы обжимается некоторое время, зависящее от вида грунта, нормальным приложением Ϭ=Ϭ'=0,1 мПа. Будем теперь в подвижной обойме отдельными ступенями прикладывать сдвигающую силу τ через соответствующую рычажную систему.

Под действием приложенной ступени горизонтальной сдвигающей силы подвижная часть грунта начнет перемещаться относительно подвижной. За величиной перемещения наблюдают с помощью специальных измерителей (индикаторов часового типа).

Предельное сопротивление грунта сдвигу выражается в виде предельных касательных напряжений τ_пр=f(Ϭ) и определяется на приборах непрерывного нагружения. По результатам испытаний строят диаграмму, откладывая по вертикальной оси предельное сдвигающее напряжение τ, а по горизонтальной Ϭ уплот. Давление.

Диаграмма предельных сопротивлений сдвигу для сыпучих грунтов может быть принята за прямую, исходящую из начала координат (для идеально сыпучих грунтов), и наклоненную под углом φ к оси давлений

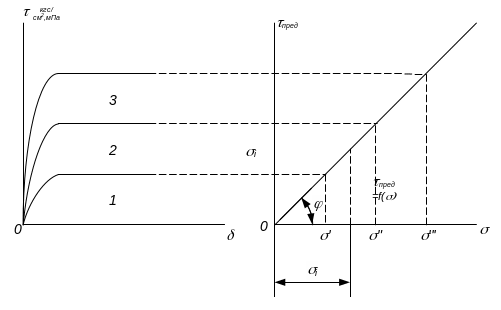
Рис. 3.9. Кривые сопротивлений сдвигу сыпучих грунтов

а)- перемещений S при сдвиге (1-3 при различных давлениях); б) — предельных сопротивлений сдвигу τ_пр=f(Ϭ)

Согласно диаграмме сдвига для сыпучих грунтов, любое предельное сдвигающее напряжение τ_предi=Ϭ_i*tgφ.

Или, обозначив коэффициент пропорциональности tgφ=f,

получим τ_предi=f*Ϭ_i.

Так как сопротивление сыпучих грунтов сдвигу есть сопротивление их трению, то угол φ носит название угла внутреннего трения, а величина f= tgφ – коэффициент внутреннего трения.

Последнее соотношение является основной прочностной зависимостью для сыпучих грунтов, установленной в 1773г Шарлем Кулоном, и формулируется следующем образом: «Предельное сопротивление сыпучих грунтов сдвигу есть сопротивление трению, прямо пропорциональное нормальному давлению.»

Связные грунты (глины, суглинки и супеси) отличаются от грунтов несвязных (сыпучих) тем, что частицы и агрегаты частиц этих грунтов связаны между собой пластичными и частично жесткими связями, при этом сопротивление их сдвигу будет в высокой степени зависеть от их связности (сил сцепления).

Основными видами испытаний связных грунтов на сдвиг будут испытания: по закрытой системе (неконсолидированно — недренированные) и по открытой системе (консолидированно — дренированные).

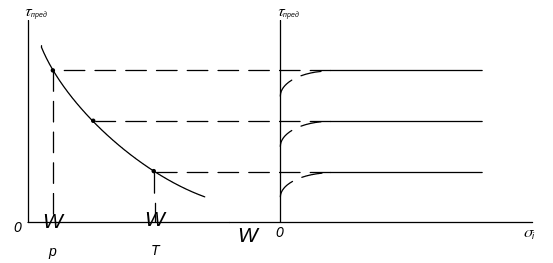
Рис. 3.10 Кривые предельных сопротивлений сдвигу связных глинистых грунтов в условиях закрытой системы.

а- зависимость сопротивления сдвигу от влажности; б- кривая сдвига при быстром (недренированном) срезе.

Кривая (а) показывает существенное влияние плотности — влажности грунта на его сопротивление сдвигу. Вторые кривые (б) константируют, что при недренированном испытании и сохранении влажности грунта предельное сопротивление сдвигу (перед τ) практически не зависит от величины внешнего давления (сжимающего напряжения Ϭ), изменяясь при изменении плотности-влажности грунта.

Другой характер имеют кривые сдвига связных грунтов, испытываемых по открытой (консолидированно-дренированной) системе.

Как показывают многочисленные испытания, кривая консолидированного сдвига связных грунтов изменяется в довольно большом диапазоне давлений, удовлетворяющих строительную практику (от Ϭ_о≈0,5 до Ϭ_φ=5-7 кгс/см²≈0,5-0,7 мПа)

Диаграмма предельных сопротивлений сдвигу для связных (глинистых) грунтов, исходящая из точки Ϭ`, может быть принята за наклонную под углом φ к оси давления, согласно которой предельное сдвигающее напряжение.

τ _предi=с+ tgφ* Ϭ_i, а т.к. tgφ=f, то уравнение приобретает следующий вид:

τ _предi=с+f*Ϭ_i, где τ _предi – предельное сопротивление сдвигу; tgφ=f – коэффициент внутреннего трения.

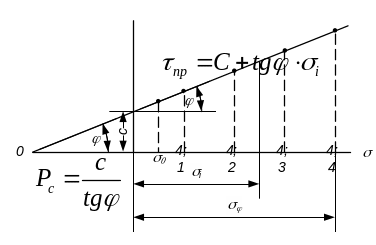
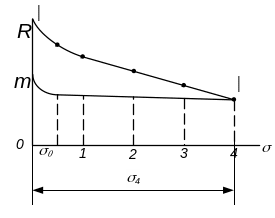
Рис. 3.11. Кривая предельных сопротивлений сдвигу связных глинистых грунтов в условиях открытой системы

Уравнение выражает закон Кулона для связных грунтов и формируется следующим образом: предельное сопротивление сдвигу связных грунтов при завершенной их консолидации есть функция первой степени от нормального давления (сжимающего напряжения)

Сопротивляемость сдвигу S_рω, как величина удельного сопротивления сдвигу имеет размерность кгс/см²(мПа).

Необходимо отметить различия в понятиях сопротивления и сопротивляемости грунта сдвигу.

Сопротивление S сдвигу некоторого объема грунта со сдвигом его по некоторой поверхности на данной площадке определяется как

S=S_рω*ω (3.17)

Сопротивляемость грунтов сдвигу в общем виде с учетом влияния у плотности – влажности можно представить:

S_рω-е=р* tgφ*ω+Σ ω+с_с, (3.18)

Где р – нормальное напряжение по данной площадке;

φ_ω-е – угол внутреннего трения при влажности ω и плотности е

(коэффициент пористости)

Σ ω-е – связность породы водно-коллоидной природы и обоатимого

характера при влажности ω и плотности е

с_с – жесткое структурное сцепление с характером необратимых связей.

S_рω, Σ ω и с_с имеют размерность напряжений. Соответствующие индексы, S_рω, φ _ω-е, Σ ω указывают на зависимость всех этих показателей от влажности ω, а сопротивляемость породы сдвигу S_рω – в общем случае и от величины нормального напряжения р.

Таким образом, сопротивляемость породы сдвигу и её прочность в общем случае определяются: 1) силами внутреннего трения в породе, зависящими от величины нормального напряжения р; 2) связностью Σ ω породы; 3) величиной свойственного ей структурного сцепления с_с.