Метод прогонки

Одним из наиболее часто используемых методов решения систем линейных алгебраических уравнений является метод последовательных исключений Гаусса. Запишем систему уравнений для неявной схемы

(8)

граничные условия на левой поверхности пластины:

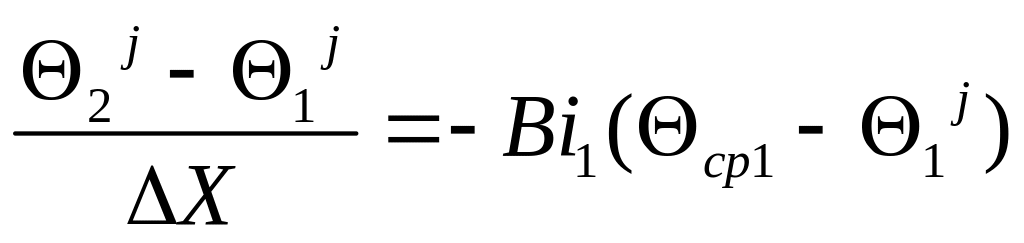(9)

граничные условия на правой поверхности пластины:

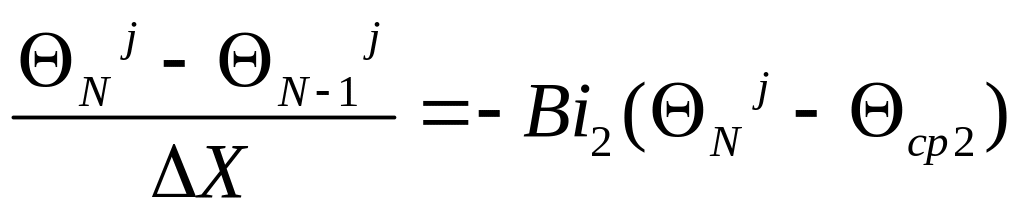(10)

Запишем уравнения входящие в систему в каноническом виде:

для граничной точки i=1 (X=0) (10) в следующем каноническом виде:

(11)

Для внутренних точек I=2,…,N-1 выражение (8) примет вид:

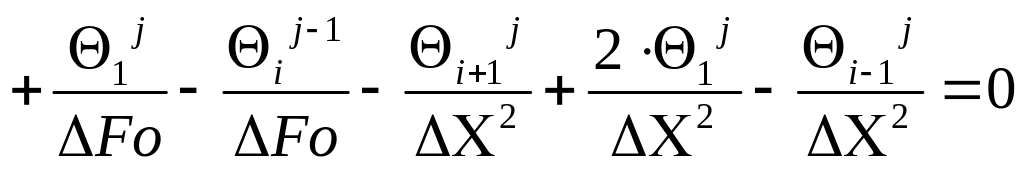
(12),

а для граничной точки i=N (X=1) (из выражения 10)

(13)

Введем новые обозначения:

; ; ; .

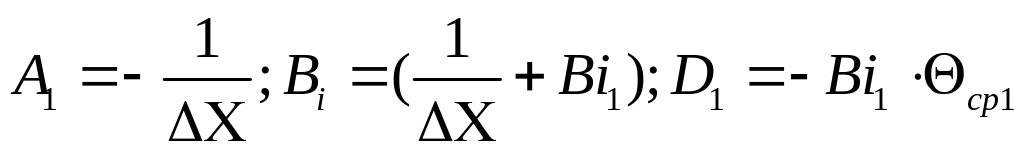
С учетом обозначений переписываем систему (11) – (13):

(14)

(15)

(16)

Выражения для получаем из соответствующих уравнений разностной схемы (8). Надо рассмотреть систему уравнений, в каждую из которых входят по 3 неизвестных, номера которых отличаются на единицу (12), а в уравнения 9 и 10 по два «соседних» неизвестных, т.е. отличными от нуля являются коэффициенты, стоящие на основной диагонали и на двух прилегающих к ней.

Для решения систем уравнений с трехдиагональной матрицей используется модифицированный метод Гаусса, называемый методом прогонки. Применим этот метод для решения системы (14) – (16). Из уравнения (14) выразим Θ₁ через Θ₂, получим

,

где

Аналогично, для i=2, получаем

Представим Θ₂ через Θ₃ следующим образом:

,

где

Подробную процедуру проводим для i=3,…,N-2. В результате получаем рекуррентные соотношения, связывающие температуры в точках i и (i+1):

(17)

и коэффициенты

(18)

Начальные значения E₁ и F₁ определяются из граничных условий (9) при i=1.

Определим E₁ и F₁ из граничных условий при Х=0:

(19)

согласно соотношению (12)

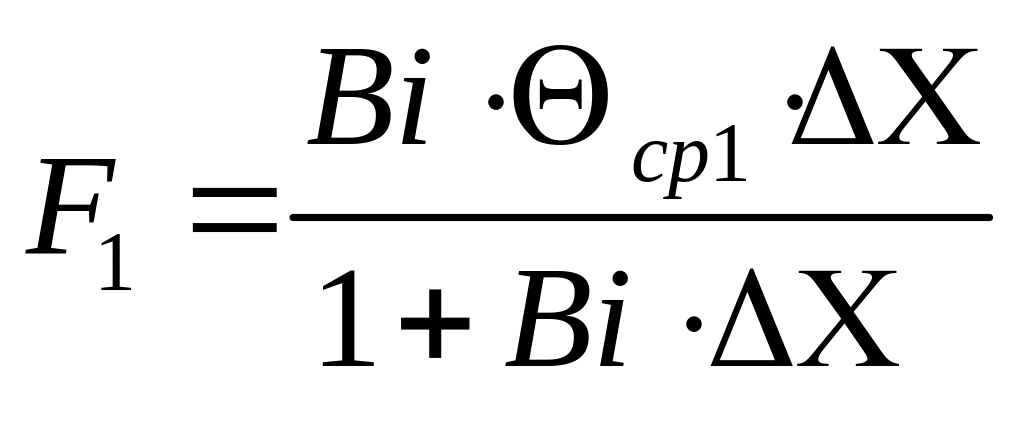
После вычислений всех коэффициентов E_i и F_i для точек i=2,…,N, определим Θ_N из граничных условий (16) при Х=1:

Двигаясь от точки i=N к точкам (N-1), (N-2),…,1, определяем значение Θ по формуле (17).

Алгоритм метода прогонки может быть сформулирован следующим образом:

1. Определяются коэффициенты E₁ и F₁ из уравнения (14) при Х=0;

2. Вычисляются E_i и F_i для точек i=2,…,N по формуле (18);

3. Определяется Θ_N из граничных условий при Х=1 по формуле (16);

4. Определяется значение Θ_i по формуле (17).

Вычисление по пунктам 1, 2 называют прямым ходом прогонки, а по пунктам 3, 4 – обратным ходом.

Программная реализация численного решения одномерных нестационарных задач

Описанный алгоритм реализуется в виде программы на языке FORTRAN.

К исходным данным относятся шаг по координате – ΔХ (выбирается произвольно, путем разбиения интервала [0;1] на (N-1) участков), шаг по времени – ΔFo (время нагрева делится на M точек), начальное значение температуры Θ₀, температуры среды Θ_ср1 и Θ_ср2 и значения безразмерных критериев Bi₁ и Bi₂, а также конечное время нагрева Fo_м.

После ввода исходных данных производится первое заполнение массива температур, в которое записывается начальное распределение Θ_i=Θ₀, i=1,...,N.

На каждом шаге по времени для нахождения разностного значения Θ_i^j методом исключения Гаусса требуется решать систему N уравнений, что и реализуется алгоритмом. Производится печать температур на каждом шаге по времени. Процедура повторяется до конечного времени Fo_м.

Пользуясь изложенным методом, можно получить решение для других задач нестационарной теплопроводности (многомерные задачи, задачи с неклассической геометрией рассматриваемого объекта и др.) и теплообмена.