Задание

Рассчитать нестационарное одномерное температурное поле в неограниченной пластине толщиной L. Начальное распределение температуры t₀ задано. Нестационарное температурное поле формируется под воздействием граничных условий на левой ( ) и правой ( ) поверхностях пластины (рис.1.).

Исходные данные (вариант№4)

1. Начальная температура тела ;

2. Коэффициент теплопроводности ;

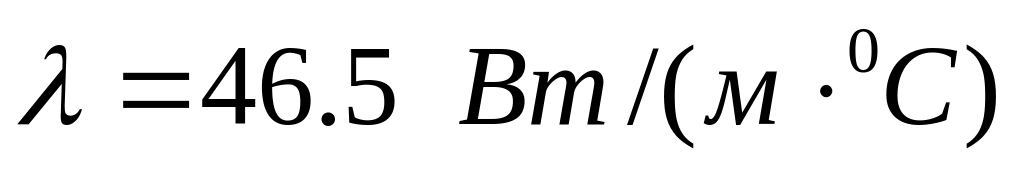3. Коэффициент температуропроводности ;

4. Толщина пластины ;

5. Время нагрева ;

6. Плотность материала пластины ;

7. Удельная теплоемкость материала пластины ;

8. Коэффициент теплоотдачи ;

9. Коэффициент теплоотдачи ;

10. Температура среды ;

11. Температура среды

Температурные условия на поверхности:

Начальное распределение температуры

t₀

0 L

Рис.1. Неограниченная пластина

Содержание

1. Введение………………………………………………………….стр. 4.

2. Постановка задачи……………………………………………….стр. 5.

3. Приведение задачи к безразмерному виду…………………….стр. 6.

4. Метод конечных разностей……………………………………..стр. 8.

5. Метод прогонки………………………………………………….стр. 10.

6. Программная реализация численного решения одномерных нестационарных задач……………………………………………………………стр. 13.

7. Текст программы…………………………………………………стр. 14.

8. Комментарии к программе………………………………………стр. 16.

9. Результаты расчетов ……………………………………………..стр. 17.

10. Кривые распределения………………………………………….стр. 18.

11. Вывод и анализ результатов…………………………………….стр. 19.

12. Список литературы………………………………………………стр. 20.

Введение

Необходимость решения задач нестационарного теплообмена встречается во многих практических ситуациях. При различных процессах обработки материалов и полуфабрикатов требуется, чтобы продукт нагревался или охлаждался во время его производства. Топки нагревательных агрегатов и печи работают циклично, и при этом происходят нестационарные изменения их содержимого и стенок печи. Часто нагревают и охлаждают материалы, чтобы получить требуемые физические свойства, суточные и сезонные изменения температуры претерпевают здания и технологические конструкции. Для улучшения их качества требуется создавать сложные математические модели, которые не всегда возможно решить аналитически.

Поставленные задачи реализуются с использованием тех или иных численных методов определения тепловых потоков и температур, изменяющихся в пространстве и времени. Приобретение навыков практического использования одного из этих методов, метода конечных разностей, посвящена данная работа.