Тема. Основные теоремы теории вероятностей план

1 Вероятность суммы несовместных событий.

2 Вероятность произведения независимых событий.

3 Вероятность произведения двух зависимых событий.

4 Вероятность суммы совместных событий.

5 Примеры задач на теоремы сложения и умножения вероятностей.

Вероятность суммы несовместных событий

Теорема. Вероятность суммы конечного числа попарно несовместных событий равна сумме вероятностей этих событий.

Теорема сложения вероятностей применима к любому конечному числу несовместных событий. Ее удобно записать в виде:

Следствие 1. Если события образуют полную группу попарно несовместных событий, то сумма их вероятностей равна единице: .

Следствие 2. Сумма вероятностей противоположных событий равна единице: .

Пример 1. В лотерее 1000 билетов. Из них на один билет попадает выигрыш 500000 рублей, на 10 билетов – выигрыши по 100000 рублей, на 50 билетов – выигрыши по 20000 рублей и на 100 билетов – выигрыши по 5000 рублей, остальные билеты невыигрышные. Некто покупает один билет. Вычислить вероятность выиграть не менее 20000 рублей.

Решение.

1-ый способ:

1. Событие - выиграть не менее 20000 рублей.

2. Событие - выиграть 20000 рублей, .

Событие - выиграть 100000 рублей, .

Событие - выиграть 500000 рублей, .

3. .

4. 

Ответ: 0,061.

2-ой способ:

1. Событие - выиграть не менее 20000 рублей.

2. Событие - выиграть меньше 20000 рублей.

3. - выиграть 5000 рублей, .

4. 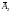- не выиграть, .

5. ,

6.

7.

Ответ: 0,061.

Пример 2. При приемке партии из 80 изделий, среди которых 6 бракованных, проверяется 40 наудачу выбранных изделий. Определить вероятность того, что партия будет принята, если условиями приема допускается бракованных изделий не более двух.

Решение.

1. Событие - партия будет принята.

2.Событие - среди 40 изделий нет ни одного бракованного,

.

Событие - среди 40 изделий есть одно бракованное,

.

Событие - среди 40 изделий есть два бракованных,

.

3. .

Ответ: 0,337.

Пример 3. Производится один выстрел по круговой мишени, состоящей из трех зон: I, II, III. Вероятность попадания при одном выстреле в зону I – 0,11, в зону II – 0,24 и в зону III – 0,35. Вычислить вероятность промаха.

Решение.

1. Событие - промах.

2. Событие - попадание в мишень.

Событие - попадание в зону I, .

Событие - попадание в зону II, .

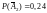Событие - попадание в зону III, .

3. .

4. 

Ответ: 0,3.

Вероятность произведения независимых событий

Теорема. Вероятность произведения двух независимых событий и равна произведению вероятностей этих событий.

Пример 1. Студент отвечает на первый вопрос с вероятностью 0,7 и на второй – с вероятностью 0,8. Студент сдаст экзамен, если ответит на оба вопроса. Вычислить вероятность того, что студент сдаст экзамен.

Решение.

1. Событие - студент сдаст экзамен.

2. Событие - студент ответит на первый вопрос, .

Событие - студент ответит на второй вопрос, .

3. .

4. 

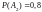Ответ: 0,56.

Теорема умножения вероятностей может быть обобщена на случай произвольного числа независимых событий и принимает вид:

,

т.е. вероятность произведения независимых событий равна произведению вероятностей этих событий.

Применяя знак произведения, теорему можно записать в виде:

Пример 2. Прибор состоит из трех узлов, каждый из которых, независимо от других, может отказать. Отказ хотя бы одного узла приводит к отказу прибора в целом. Вероятность безотказной работы первого узла равна ; второго ; третьего . Вычислить вероятность безотказной работы прибора в целом.

Решение.

1. Событие - безотказная работа прибора.

2. Событие - безотказная работа 1-го узла, .

Событие - безотказная работа 2-го узла, .

Событие - безотказная работа 3-го узла, .

3. .

4. 

Ответ: 0,504.