«Согласовано» Директор НТЦ ВС ОАО «ICL –КПО ВС» _________________ И. В. Кульмяков «___» ________________ 2012 г. |
«Утверждено» Директор КЭТС ______________ Н. Н. Китаева «___» ________________ 2012 г. |
Приложение №1
Перечень
вопросов к итоговой государственной аттестации
специальности 230105 – «Программное обеспечение вычислительной техники и автоматизированных систем».
Теоретические вопросы по дисциплине:
«Математические методы»
Линейное программирование. Общий вид задач линейного программирования. Основная задача линейного программирования.
Симплекс- метод.
Сведение произвольной задачи линейного программирования к ОЗЛП.
Транспортная задача. Открытая транспортная задача. Закрытая транспортная задача.
Нелинейное программирование. Общий вид задач нелинейного программирования. Метод множителей Лагранжа.
Динамическое программирование. Основные понятия динамического программирования. Шаговое управление, управление операцией в целом. Оптимальное управление, выигрыш на данном шаге, выигрыш за всю операцию. Идея метода динамического программирования. Простейшие задачи, решаемые методом динамического программирования.
Задача о нахождении кратчайших путей в графе и методы ее решения. Основные определения и характеристики графа. Матрица смежности, матрица инцидентности. Задача о нахождении кратчайших путей в графе и методы ее решения.
Задача о максимальном потоке и алгоритм Форда - Фалкерсона.
Системы массового обслуживания. Основные понятия теории марковских процессов: случайный процесс, марковский процесс, граф состояний, поток событий, вероятность состояния. Уравнение Колмогорова. Финальные вероятности состояний. Схема гибели и размножения. Понятие системы массового обслуживания, классификация систем массового обслуживания. Простейшие системы массового обслуживания и их параметры. Основные теоремы двойственности. Симметричные двойственные задачи. Несимметричные двойственные задачи. Смешанные двойственные задачи.
Задача о назначениях.
Практические вопросы по дисциплине: «Математические методы»
Найти оптимальное решение задачи математическая модель которой имеет вид:
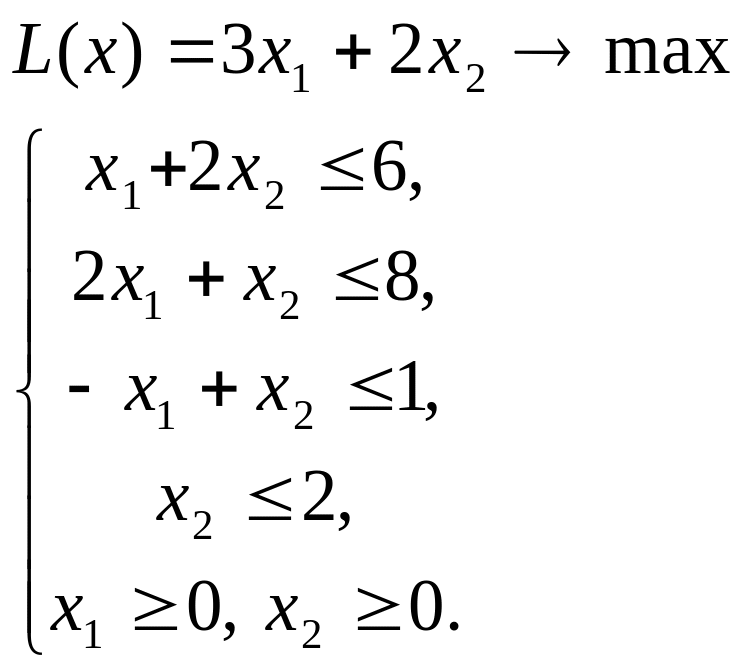
Найти оптимальное решение задачи, математическая модель которой имеет вид
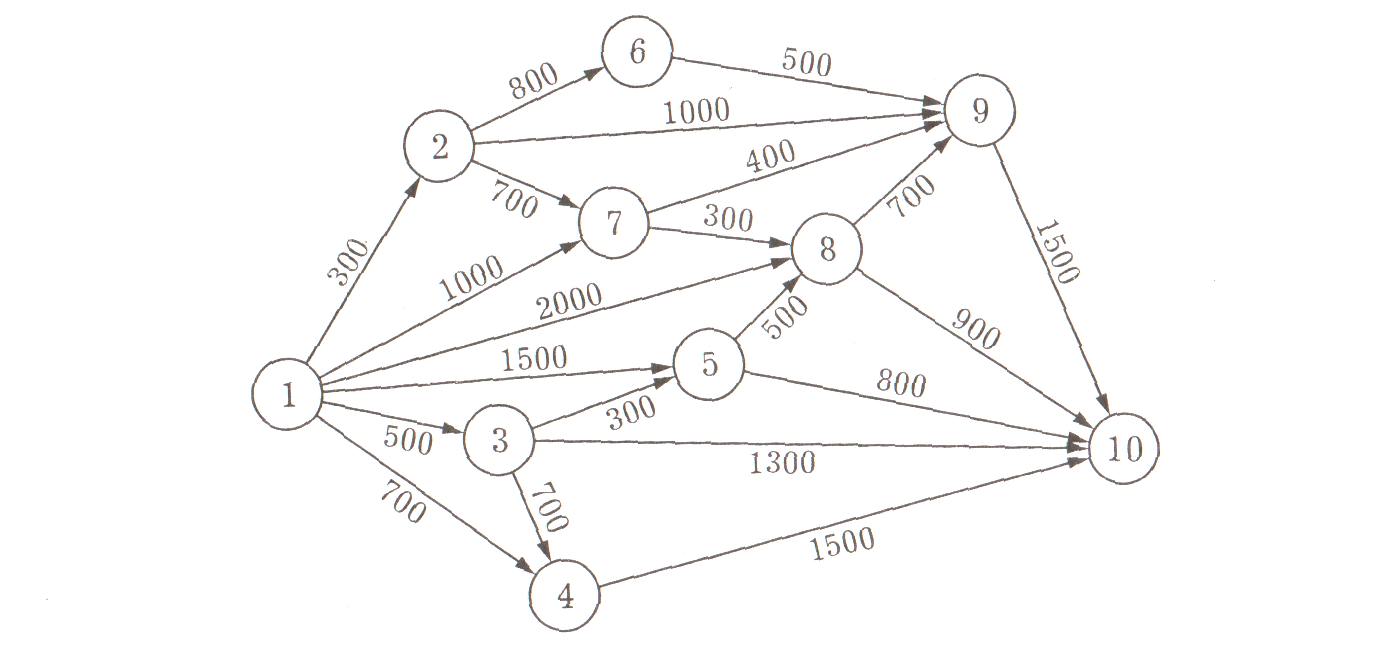
Строительной фирме необходимо проложить водопроводные трубы к девяти объектам, на которых она ведет строительство. Числа на ребрах указывают длину труб в метрах. Узел 1 – подсоединен к водопроводной трассе. Отсутствие ребра между двумя узлами означает, что соединение соответствующих объектов невозможно. найти соединение узла 1 с объектами строительства, чтобы суммарная длина трубопроводов была минимальной.
Решить задачу симплексным методом.
(Решение двойственных задач , симметричные задачи) Составить математическую модель двойственной задачи, решив одну из них, найти оптимальное решение другой.
(Решение двойственных задач , несимметричные задачи) Составить математическую модель двойственной задачи, решив одну из них, найти оптимальное решение другой.
(Решение двойственных задач , смешанные задачи) Составить математическую модель двойственной задачи, решив одну из них, найти оптимальное решение другой.
На складах
имеются запасы продукции в количествах
90,400, 110 соответственно. Потребители
должны
получить эту продукцию в количестве
140, 300, 160 т соответственно. Найти такой
вариант поставок, при котором сумма
затрат на перевозки была бы минимальной.
Расходы по перевозке 1 т продукции
заданны матрицей (ден. ед.)
Организация поставляет бутылки на четыре завода, которые производят прохладительные напитки. Она имеет три склада, причем на складе 1 находятся 6000 бутылок. на складе 2 – 3000 бутылок и на складе 3 – 4000 бутылок. Первому заводу требуется 4000 бутылок, второму заводу – 5000 бутылок, третьему заводу – 1000 бутылок, четвертому заводу – 3000 бутылок.
Матрицей заданна стоимость перевозки (ден. ед.) одной бутылки от каждого склада к каждому заводу:
Как следует организовать доставку бутылок на завод, чтобы стоимость перевозки была минимальной?
Составить оптимальный план перевозки грузов от трех поставщиков с грузами 240, 40, 110 т к четырем потребителям с запросами 90, 190, 40 и 130 т. Стоимость перевозок единицы груза от каждого поставщика к каждому потребителю заданна матрицей
Дана матрица ресурсов
Распределить ресурсы матрицы С по четырем объектам.
Цех имеет пять станков разных типов, каждый из которых может выполнять пять различных операций по обработке деталей. Известна производительность
каждого станка при выполнении каждой
операции, заданная матрицей
Определить, какую операцию, и за каким станком следует закрепить, чтобы суммарная производительность была максимальной при условии, что за каждым станком закреплена только одна операция.
Заводы некоторой автомобильной фирмы расположены в городах А, В и С. Основные центры распределения продукции сосредоточенны в городах D и E. Объемы производства указанных трех заводов равняются 1000, 1300 и 1200 автомобилей ежеквартально. Величины квартального спроса в центрах распределения составляют 2300 и 1400 автомобилей соответственно. Стоимость перевозки автомобилей по железной дороге по каждому из возможных маршрутов приведены в таблице