Тесты по дисциплине «Теория игр»

1. Антагонистическая игра это …

   1. Игра с не нулевой суммой

   2. Биматричная игра

   3. Игра с нулевой суммой

   4. Статистическая игра

   5. Игра с природой

2. Конечная игра двух игроков с нулевой суммой называется …

   1. Биматричной игрой

   2. Кооперативной игрой

   3. Дифференциальной игрой

   4. Матричной игрой

   5. Конечномерной игрой

3. Количество игроков в матричной игре равно …

4. Матричная игра имеет решение в чистых стратегиях, если … (отметить все верные условия)

   1. Нижняя чистая цена игры больше верхней чистой цены игры

   2. Игра имеет седловую точку

   3. Нижняя чистая цена игры меньше верхней чистой цены игры

   4. Игра не имеет седловой точки

   5. Нижняя чистая цена игры и верхняя чистая цена игры равны

5. Упрощение платежной матрицы некоторой матричной игры возможно за счет …

   1. Исключения отрицательных стратегий

   2. Построения графической интерпретации игры

   3. Исключения оптимальных чистых стратегий

   4. Сведения матричной игры к задаче линейного программирования

   5. Исключения доминируемых стратегий

Общие вопросы решения матричных игр в смешанных стратегиях

1. Решение матричной игры в смешанных стратегиях целесообразно, если

   1. Игра повторяется один раз

   2. Игра имеет седловую точку

   3. Игра повторяется большое число раз

   4. Нижняя и верхняя цены игры равны

2. Выберите верное утверждение

   1. Любая матричная игра имеет решение в чистых стратегиях

   2. Любая матричная игра имеет решение, по крайней мере, в смешанных стратегиях

   3. В любой матричной игре есть доминируемые стратегии

   4. В любой матричной игре есть седловая точка

Свойства цены матричной игры

3. Если  – нижняя чистая цена игры,  – верхняя чистая цена игры, то для любой матричной игры верно неравенство:

   1.  < 

   2.   

   3.  > 

   4.   

4. Установите соответствие между значениями нижней и верхней чистыми ценами игры и допустимой ценой игры для некоторой платежной матрицы

   1.  = -2;  = 0 1)  = -2,4

   2.  = -5;  = -1 2)  = 1,35

   3.  = 3;  = 7 3)  = -1,25

4)  = 3

Свойства смешанных стратегий игроков в матричных играх

1. Сумма компонентов любой смешанной стратегии игрока в произвольной матричной игре равна …

2. Выберите смешанную стратегию, которая может быть решением некоторой игры для игрока А:

   1. 

   2. 

   3. 

   4. 

Преобразование платежной матрицы

3. Если все элементы платежной матрицы преобразовать по формуле 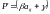, то …

   1. Оптимальные стратегии игроков не изменятся

   2. Все компоненты оптимальных стратегий надо умножить на 

   3. Ко всем компонентам оптимальных стратегий надо прибавить 

   4. Все компоненты оптимальных стратегий надо умножить на  и прибавить к ним 

4. Если у матричной игры с платежной матрицей цена игры равна 1,65, тогда цена игры, заданной матрицей равна …

5. Цена игры с платежной матрицей равна 550. Цена игры с платежной матрицей равна …

   1. 450

   2. 550

   3. 5,5

   4. 6,5

6. Установите соответствие между платежными матрицами с одинаковыми ценами игры

1)	А)
2)	В)
	С)

Свойства симметричных игр

7. Если элементы платежной матрицы удовлетворяют условию 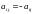, то соответствующая матричная игра называется …

   1. Кососимметричной

   2. Симметричной

   3. Рефлексивной

   4. Элементарной

8. Цена симметричной матричной игры равна …

9. У симметричных матричных игр смешанные стратегии игроков …

   1. Совпадают

   2. Различны

   3. Симметричны

   4. Асимметричны

Решение матричных игр сведением к задаче линейного программирования

1. Для решения матричной игры как задачи линейного программирования необходимо, чтобы …

   1. Цена игры была положительной

   2. Игра имела размерность 2х2

   3. Сумма компонентов смешанных стратегий игроков равнялась 1

   4. Игра не имела решения в чистых стратегиях

Принятие решений в условиях неопределенности

6. Задача принятия решений в условиях неопределенности, когда игрок взаимодействует с окружающей средой называется …

   1. Антагонистической игрой

   2. Игрой в нормальной форме

   3. Игрой с природой

   4. Позиционной игрой

7. Установите соответствие между названием критерия принятия решения и формулой, по которой рассчитываются оценки стратегий игрока

1) Критерий максимального математического ожидания	А)
2) Критерий недостаточного основания Лапласа	В)
3) Максиминный критерий Вальда	С)
	D)