2. Формулы Лапласа. Формула Пуассона

При больших значениях n использование формулы Бернулли связано с трудоёмкими вычислениями. Пусть нам нужно вычислить :

Ясно, что это технически сложно. В подобных случаях используют формулу, являющуюся предельным случаем формулы Бернулли.

Локальная формула Лапласа. Если вероятность p появления события A постоянна в каждом испытании и отлична от 0 и 1, то вероятность того, что событие A наступит k раз в n независимых испытаниях, при достаточно большом числе n приближенно равна

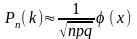, (2.3)

где – функция Гаусса (рисунок 2.2), .

Рисунок 2.2

Чем больше n, тем точнее формула (2.3). При она даёт удовлетворительные для практики результаты.

Значения функции Гаусса приведены в таблице Б.1 приложения Б.

Свойства функции Гаусса:

1. – четная функция, т.е. .

2. функция монотонно убывает при положительных значениях x, причем при (практически можно считать, что уже при ).

Пример 2.3. Вероятность изготовления детали высшего сорта на данном станке равна 0,4. Найти вероятность того, что среди наудачу взятых 56 деталей половина окажется высшего сорта.

Решение. n большое, 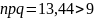, поэтому применим локальную формулу Лапласа (2.3). Проведём необходимые вычисления:

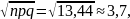
Следующая формула Лапласа позволяет находить вероятность того, что событие A в n независимых испытаниях наступит не менее и не более раз.

Интегральная формула Лапласа. Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие A в n независимых испытаниях наступит не менее и не более раз, при достаточно большом числе n приближенно равна

(2.4)

– функция Лапласа, (2.5)

(2.6)

При формула (2.4) дает, как правило, удовлетворительную для практики погрешность вычисления вероятности.

Значения функции можно найти в таблице Б.2 приложений. График изображён на рисунке 2.3. Перечислим свойства функции Лапласа.

1.Функция нечетная, т. е. .

2.Функция монотонно возрастает, при (практически можно считать, что уже при ).

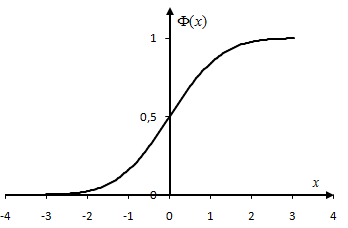
Рисунок 2.3

Пример 2.4. В некоторой местности из каждых 100 семей 80 имеют холодильник. Какова вероятность, что от 300 до 360 семей включительно из 400 обследованных имеют холодильники?

Хорошо бы пример технический

Решение. Применим интегральную формулу Лапласа ( . Вначале определим по формулам (2.6)

.

Далее по формуле (2.4), учитывая свойства функции Φ(x), получим:

.

(Из таблицы Б.2 приложения Б: ).

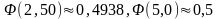Рассмотрим следствие интегральной формулы Лапласа.

Следствие. Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то при достаточно большом числе независимых испытаний вероятность следующих событий определяются по формулам:

а) относительная частота события A заключена в пределах от  до :

(2.7)

б) относительная частота события A отличается от его вероятности 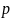не более, чем на величину (по абсолютной величине):

При и формулы Лапласа дают удовлетворительную для практики погрешность вычисления вероятности. Если n одного порядка с 1/n при больших n, или , более точный результат дает формула Пуассона

, (2.9)

где .

Пример 2.5. На факультете 730 студентов. Какова вероятность того, что 1 сентября является днём рождения одновременно трёх студентов?

Решение. Вероятность того, что день рождения для отдельного студента 1 сентября, равна p=1/365<0,1. Применяем формулу Пуассона (2.7). В нашем случае n=730, p=1/365, k=3, поэтому

.

Таким образом, в среднем в 18 случаях из ста на 1 сентября приходится день рождения трёх студентов факультета.

Пример 2.6. вероятность появления события в каждом из 400 независимых испытаний равна 0,8. Найти такое число , чтобы с вероятностью 0,9876 абсолютная величина отклонения относительной частоты появления события от его вероятности 0,8 не превысила

Решение. По условию Подставим в формулу (2.8):

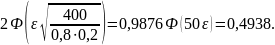
По таблице значений функции Лапласа находим

1. Доля изделий высшего сорта на данном предприятии составляет 87%. Сколько изделий высшего сорта следует ожидать в случайно отобранной партии из 400 изделий? (348.)

2. Сколько нужно взять деталей, чтобы наивероятнейшее число годных деталей было равно 50, если вероятность того, что наудачу взятая деталь будет бракованной, равна 0,1? (55 или 56.)

3. Из большой партии изделий берут на пробу 10 штук. Известно, что доля нестандартных изделий во всей партии составляет 10%. Какова вероятность, что среди отобранных стандартных изделий будет 8? (0,194.)

4. Среди изделий некоторого цеха брак встречается с вероятностью 0,015. Найти вероятность, что среди 200 изделий бракованных окажется: а) 5; б) не более 5. (а) 0,1008; б) 0,916.)

5. На каждую 1000 букв русского в среднем приходится 110 букв «о». Какова вероятность, что в тексте из 4000 букв буква «о» встретится от 400 до 500 раз? (0,97795)

6. Автоматическая штамповка клемм для предохранителей даёт 10% отклонений от заданного стандарта. Сколько стандартных клемм следует ожидать с вероятностью 0,0587 среди 400 клемм? (3603.)

7. Отдел технического контроля проверяет на стандартность 900 деталей. Вероятность того, что деталь стандартна, равна 0,9. Найти с вероятностью 0,9544 границы, в которых будут заключено число k стандартных деталей среди проверенных. ( )

8. На тарелке лежат три апельсина, пять яблок и четыре груши. Дети съели 4 фрукта. Какова вероятность, что они съели: а) апельсин, два яблока и грушу; б) 4 яблока; в) по крайней мере, два яблока? (Ответ: а) 8/33; б) 1/99; в) 19/33.)

9. В ящике находятся катушки с нитками четырех цветов: белого –50%, красного – 20%, зеленого – 20%, синего –10%. Какова вероятность, что взятая наудачу катушка окажется с нитями синего или зеленого цвета? (Ответ: 0,3)

10. Отдел технического контроля обнаружил пять бракованных книг в партии из случайно отобранных 100 книг. Найти относительную частоту появления бракованных книг. (Ответ: .)

11. Пятитомное собрание сочинений расположено на полке в случайном порядке. Какова вероятность того, что книги стоят слева направо в порядке нумерации (от 1 до 5)? (Ответ: 1/120.)

12. Из ящика, содержащего 5 пар обуви, из которых 3 пары мужской, а две пары женской обуви, перекладывают наудачу две пары в другой ящик, содержащий одинаковое количество пар женской и мужской обуви. Какова вероятность, что во втором ящике после этого окажется одинаковое количество пар мужской и женской обуви? (Ответ: 0,6.)

13. Страховая компания разделяет застрахованных клиентов по классам риска: I класс – малый риск, II класс – средний, III класс – большой риск. Среди застрахованных клиентов 50% первого класса риска, 30% – второго и 20№ – третьего. Вероятность необходимости выплачивать страховое вознаграждение для первого класса равна 0,01, второго – 0,03, третьего – 0,08. Найти вероятность того, что: а) застрахованный получит денежное вознаграждение за период страхования; б) получивший денежное вознаграждение застрахованный относится к группе малого риска. (Ответ: а) 0,03; б) 0, 167.)

14. В группе из 20 студентов, пришедших на экзамен. 6 подготовлены отлично, 8 – хорошо, 4 – посредственно и 2 – плохо. В экзаменационных билетах имеется 40 вопросов. Отлично подготовленный студент может ответить на все 40 вопросов, хорошо подготовленный – на 32 , посредственно – на 20, плохо – на 10. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что студент подготовлен: а) отлично; б) плохо. (Ответ: а) ; б) .)

Примерный вариант контрольной работы

1. Общество из 15 человек садится за круглый стол. С какой вероятностью два определённых лица окажутся рядом? ( .)

2. Из 18 стрелков шесть попадают в мишень с вероятностью 0,8, восемь – с вероятностью 0,7, а остальные – с вероятностью 0,6. Один из стрелков сделал выстрел, но в мишень не попал. К какой из перечисленных групп вероятнее всего принадлежит этот стрелок?

( , , т.е. ко второй.)

3. Семён на охоте стреляет по зайцам. Вероятность попадания при каждом выстреле равна 0,2. Найти вероятность того, что пятым выстрелом он убьёт третьего зайца. ( .)

4. Число коротких волокон в партии хлопка составляет 25%. Какова вероятность, что в пучке из 432 волокон коротких будет не менее 100 и не более 130? ( .)

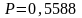5. Доля изделий высшего сорта на данном предприятии составляет 31%. Сколько изделий надо взять, чтобы наивероятнейшее число изделий высшего сорта было равно 23? (От 74 до 76 изделий.)