2. Повторные независимые испытания

Некоторые испытания называются независимыми относительно события A, если вероятность наступления события A в каждом испытании не зависит от исходов других испытаний. Если независимые повторные испытания проводятся при одном и том же комплексе условий S, то вероятность в каждом испытании одна и та же. Описанная последовательность испытаний называется схемой Бернулли – по имени швейцарского математика XVII века Якоба Бернулли.

Такая схема описывает многие реальные ситуации: 1) проверяются n изделий, событие A – появление события с браком, 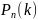– вероятность того, что среди n изделий окажется k бракованных; 2) регистрируются n новорожденных, событие A – рождение девочки, – вероятность того, что среди n новорожденных k девочек; 3) имеется n инвестиционных проектов, событие A – прибыль в первый год работы проекта, – вероятность того, что из n только k проектов принесут прибыль в первый год работы. Тогда возникает задача – вычислить искомую вероятность .

1. Формула Бернулли

Теорема. Пусть комплекс условий S воспроизводится n раз, причём каждый раз событие A может наступить с одной и той же вероятностью p (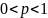 ) независимо от результатов предыдущих опытов. Тогда вероятность того, что событие A произойдёт ровно k раз в n испытаниях, определяется по формуле Бернулли

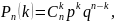(2.1)

где 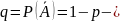вероятность не появления в одном испытании.

Доказательство. Пусть 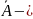соответственно появление и непоявление события A в единичном испытании, 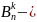событие, состоящее в том, что в n независимых испытаниях событие A появилось ровно k раз. Тогда

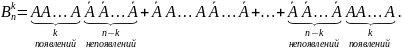
Всего получим 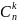слагаемых ( 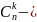сколькими способами можно расположить объектов по 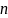местам без учета порядка). Тогда

Чтобы нагляднее представить свойства ряда вероятностей 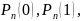…, …, 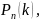, 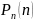в прямоугольной системе координат отмечают точки с координатами и соединяют их ломаной (рисунок 2.1).

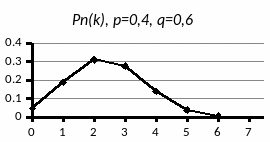
Рисунок 2.1

Число наступлений события называется наивероятнейшим, если вероятность наступления события данное число раз в этой серии испытаний наибольшая по сравнению с вероятностями других исходов. На рисунке 2.3 наивероятнейшее число .

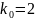Пусть n – число независимых испытаний, p – вероятность наступления события в отдельном испытании. Тогда наивероятнейшее число наступлений события 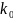удовлетворяет неравенству

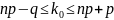, (2.2)

где .

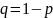Так как разность 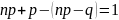, то всегда найдётся целое число , удовлетворяющее написанному выше двойному неравенству. При этом, если целое число, то наивероятнейших чисел два: 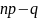и .

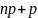Пример 2.1. Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найти наивероятнейшее число появления бракованных деталей из 5 отобранных и вероятность этого числа.

Решение. Вероятность изготовления бракованной детали 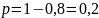. По формуле (2.2): 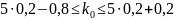или .

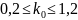Единственное целое число, удовлетворяющее этому неравенству, 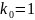, его вероятность находим по формуле Бернулли

.

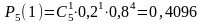Пример 2.2. Сколько раз надо подбросить игральную кость, чтобы наивероятнейшее число выпадений двойки было равно 32?

Решение. В данном случае 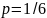, 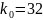. Требуется найти число независимых испытаний n. Величины 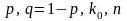связаны между собой соотношением (2.2): 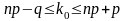, откуда

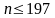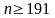Из первого неравенства , а из второго . Таким образом, необходимо провести от 191 до 197 подбрасываний игральной кости.